Lý thuyết Đường thẳng và mặt phẳng trong không gian (Cánh diều 2023) hay, chi tiết

Lý thuyết Toán lớp 11 Bài 1: Đường thẳng và mặt phẳng trong không gian
A. Lý thuyết Đường thẳng và mặt phẳng trong không gian
I. Khái niệm mở đầu
1. Mặt phẳng
(ảnh 1) (ảnh 2)
Hình ảnh mặt phẳng trong thực tiễn
– Biểu diễn một mặt phẳng: Người ta thường biểu diễn mặt phẳng bằng một hình bình hành.
(ảnh 3)
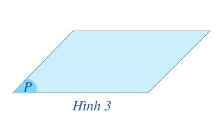
– Để kí hiệu mặt phẳng ta dùng chữ cái in hoa đặt trong dấu ngoặc ( ).
2. Điểm thuộc mặt phẳng
(ảnh 4)
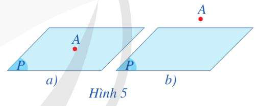
– Điểm A thuộc mặt phẳng (P), ta kí hiệu $A \in (P)$
– Điểm A không thuộc mặt phẳng (P) ta kí hiệu $A \notin (P)$ .
3. Hình biểu diễn của một hình trong không gian
a, Khái niệm
Hình được vẽ trong mặt phẳng để giúp ta hình dung được về một hình trong không gian gọi là hình biểu diễn của hình không gian đó.
b, Quy tắc vẽ hình biểu diễn của một hình trong không gian
– Đường thẳng được biểu diễn bởi đường thẳng, đoạn thẳng được biểu diễn bởi đoạn thẳng.
– Hai đường thẳng song song (hoặc cắt nhau) được biểu diễn bởi 2 đường thẳng song song (hoặc cắt nhau).
– Hình biểu diễn giữ nguyên quan hệ liên thuộc giữa điểm và đường thẳng.
– Dùng nét liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn để biểu diễn cho đường bị che khuất.
II. Các tính chất thừa nhận của hình học không gian
– Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
– Có một và chỉ một mặt phẳng đi qua 3 điểm không thẳng hàng.
– Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều nằm trong mặt phẳng đó.
– Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P) thì ta nói d nằm trong (P) hoặc (P) chứa d. Kí hiệu $d \subset (P)$ hoặc $(P) \supset d$ .
– Tồn tại 4 điểm không cùng thuộc một mặt phẳng.
– Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó. Đường thẳng đó được gọi là giao tuyến, kí hiệu $d = (P) \cap (Q)$ .
– Trên mỗi mặt phẳng, tất cả các kết quả đã biết trong hình học phẳng đều đúng.
III. Một số cách xác định mặt phẳng
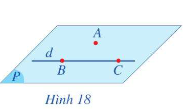
Cho điểm $A \notin d$ . Khi đó qua điểm A và đường thẳng d có một và chỉ một mặt phẳng. Kí hiệu mp(A,d) hoặc (A,d).
(ảnh 5)
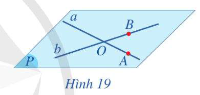
Cho hai đường thẳng a và b cắt nhau. Khi đó, qua a và b có một và chỉ một mặt phẳng, kí hiệu mp(a,b).
(ảnh 6)
IV. Hình chóp và hình tứ diện
1. Hình chóp
– Trong mặt phẳng (P), cho đa giác $A_{1} A_{2} . . . A_{n}$ $(n \geq 3)$ . Lấy điểm S nằm ngoài mặt phẳng (P). Nối S với các đỉnh $A_{1}, A_{2}, . . ., A_{n}$ để được n tam giác $S A_{1} A_{2}, S A_{2} A_{3}, . . ., S A_{n} A_{1}$ . Hình gồm đa giác $A_{1} A_{2} . . . A_{n}$ và n tam giác $S A_{1} A_{2}, S A_{2} A_{3}, . . ., S A_{n} A_{1}$ được gọi là hình chóp và kí hiệu là $S . A_{1} A_{2} . . . A_{n}$ .
– Trong hình chóp $S . A_{1} A_{2} . . . A_{n}$ :
+ Điểm S được gọi là đỉnh.
+ Đa giác $A_{1} A_{2} . . . A_{n}$ được gọi là mặt đáy.
+ Các tam giác $S A_{1} A_{2}, S A_{2} A_{3}, . . ., S A_{n} A_{1}$ được gọi là các mặt bên
+ Các cạnh $S A_{1}, S A_{2}, . . ., S A_{n}$ được gọi là cạnh bên; các cạnh $A_{1} A_{2}, A_{2} A_{3} . . ., A_{n} A_{1}$ được gọi là các cạnh đáy.
Nếu đáy của hình chóp là một tam giác, tứ giác, ngũ giác,…thì hình chóp tương ứng gọi là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác,…
2. Hình tứ diện
Cho 4 điểm A, B, C, D không đồng phẳng. Hình gồm 4 tam giác ABC, ABD, ACD và BCD được gọi là hình tứ diện, kí hiệu là ABCD.
(ảnh 7)
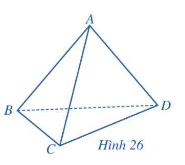
Trong đó, các điểm A, B, C, D được gọi các đỉnh của tứ diện, các đoạn thẳng AB, BC, CD, DA, BD,AC được gọi là cạnh của tứ diện; các tam giác ABC, ABD, ACD và BCD gọi là mặt của tứ diện.
Hai cạnh không có đỉnh chung được gọi là hai cạnh đối diện, đỉnh không nằm trên một mặt gọi là đỉnh đối diện với mặt đó.

B. Bài tập Đường thẳng và mặt phẳng trong không gian
Đang cập nhật …
Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 3: Hàm số liên tục
Lý thuyết Bài 1: Đường thẳng và mặt phẳng trong không gian
Lý thuyết Bài 2: Hai đường thẳng song song trong không gian
Lý thuyết Bài 3: Đường thẳng và mặt phẳng song song
Lý thuyết Bài 4: Hai mặt phẳng song song
Lý thuyết Bài 5: Hình lăng trụ và hình hộp

Xem thêm các bài tóm tắt lý thuyết chương Toán lớp 11 Cánh diều hay, chi tiết khác:
Lý thuyết Chương 1: Hàm số lượng giác và phương trình lượng giác
Lý thuyết Chương 2: Dãy số. Cấp số cộng. Cấp số nhân
Lý thuyết Chương 3: Giới hạn. Hàm số liên tục
Lý thuyết Chương 4: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

==== ~~~~~~ ====

Bài liên quan:

Leave a Comment Hủy