Lý thuyết Phép tính lũy thừa với số mũ thực (Cánh diều 2024) hay, chi tiết | Toán lớp 11

Lý thuyết Toán lớp 11 Bài 1: Phép tính lũy thừa với số mũ thực

A. Lý thuyết Phép tính lũy thừa với số mũ thực

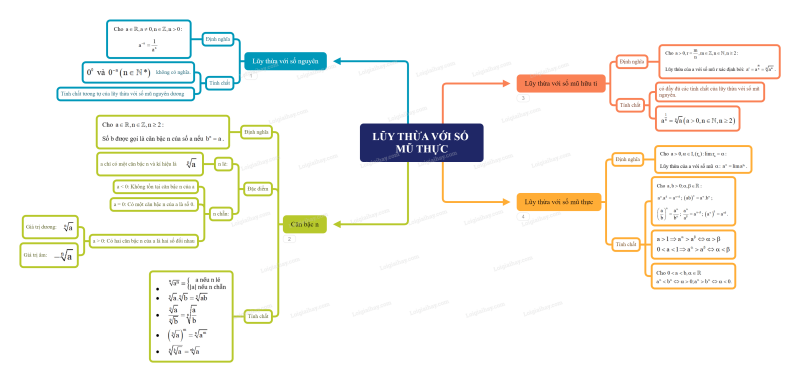
1. Phép tính lũy thừa với số mũ nguyên

Cho số thực a khác 0 và số nguyên dương n. Ta đặt $a^{-n}=\frac{1}{a^n}$.

Chú ý:

– $0^0$ và $0^{-n}$ (n nguyên dương) không có nghĩa.

– Lũy thừa với số mũ nguyên có các tính chất tương tự của lũy thừa với số mũ nguyên dương.

2. Căn bậc n

a) Định nghĩa

Cho số thực a và số nguyên dương n (n $\ge$ 2). Số b được gọi là căn bậc n của số a nếu $b^n=a$.

Nhận xét:

– Với n lẻ và a $\in \mathbb{R}$: Có duy nhất một căn bậc n của a, kí hiệu là $\sqrt[n]{a}$.

– Với n chẵn, ta xét ba trường hợp sau:

+) a < 0: Không tồn tại căn bậc n của a.

+) a = 0: Có một căn bậc n của a là số 0.

+) a > 0: Có hai căn bậc n của a là hai số đối nhau, giá trị dương kí hiệu là $\sqrt[n]{a}$, còn giá trị âm kí hiệu là $-\sqrt[n]{a}$.

b) Tính chất

• $\sqrt[n]{a^n}=\{\begin{array}{l}anếunlẻ\\ \left|a\right|nếunchẵn\end{array}$
• $\sqrt[n]{a}.\sqrt[n]{b}=\sqrt[n]{ab}$
• $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$
• ${\left(\sqrt[n]{a}\right)}^m=\sqrt[n]{a^m}$
• $\sqrt[n]{\sqrt[k]{a}}=\sqrt[nk]{a}$

(Ở mỗi công thức trên, ta giả sử các biểu thức xuất hiện trong đó là có nghĩa).

3. Phép tính lũy thừa với số mũ hữu tỉ

Cho số thực a dương và số hữu tỉ $r=\frac{m}{n}$, trong đó $m\in \mathbb{Z},n\in \mathbb{N},n\ge 2$. Lũy thừa của a với số mũ r xác định bởi: $a^r=a^{\frac{m}{n}}=\sqrt[n]{a^m}$.

Nhận xét:

• $a^{\frac{1}{n}}=\sqrt[n]{a}\left(a>0,n\in \mathbb{N},n\ge 2\right)$.
• Lũy thừa với số mũ hữu tỉ của số thực dương có đầy đủ các tính chất của lũy thừa với số mũ nguyên.

4. Phép tính lũy thừa với số mũ thực

a) Định nghĩa

Cho a là số thực dương, $\alpha$ là số vô tỉ, $\left(r_n\right)$ là dãy số hữu tỉ và $lim{r}_n=\alpha$. Giới hạn của dãy số $\left(a^{r_n}\right)$ gọi là lũy thừa của a với số mũ $\alpha$, kí hiệu $a^{\alpha }$, $a^{\alpha }=lim{a}^{r_n}$.

b) Tính chất

– Cho a, b là những số thực dương; $\alpha ,\beta$ là những số thực tùy ý. Khi đó, ta có:

$a^{\alpha }.a^{\beta }=a^{\alpha +\beta }$; ${\left(ab\right)}^{\alpha }=a^{\alpha }.b^{\alpha }$; ${\left(\frac{a}{b}\right)}^{\alpha }=\frac{a^{\alpha }}{b^{\alpha }}$; $\frac{a^{\alpha }}{a^{\beta }}=a^{\alpha -\beta }$; ${\left(a^{\alpha }\right)}^{\beta }=a^{\alpha \beta }$.

– Nếu a > 1 thì $a^{\alpha }>a^{\beta }\iff \alpha >\beta$.

Nếu 0 < a < 1 thì $a^{\alpha }>a^{\beta }\iff \alpha <\beta$.

– Cho 0 < a < b, $\alpha$ là một số thực. Ta có:

$a^{\alpha }<b^{\alpha }\iff \alpha >0$; $a^{\alpha }>b^{\alpha }\iff \alpha <0$.

B. Bài tập Phép tính lũy thừa với số mũ thực

Đang cập nhật …

Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 2: Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất

Lý thuyết Bài 1: Phép tính lũy thừa với số mũ thực

Lý thuyết Bài 2: Phép tính lôgarit

Lý thuyết Bài 3: Hàm số mũ. Hàm số lôgarit

Lý thuyết Bài 4: Phương trình mũ, bất phương trình mũ và lôgarit