Giải SGK Toán 10 Bài 2 (Cánh diều): Hệ bất phương trình bậc nhất hai ẩn

Giải bài tập Toán lớp 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Video giải Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn – Cánh diều

Câu hỏi khởi động trang 25 Toán lớp 10: Quảng cáo sản phẩm trên truyển hình là một hoạt động quan trong trong kinh doanh của các doanh nghiêp. Theo Thông báo số 10/2019, giá quảng cáo trên VTV1 là 30 triệu đồng cho 15 giây/1 lần quảng cáo vào khoảng 20h30; là 6 triệu đồng cho 15 giây/1 lần quảng cáo vào khung giờ 16h00-17h00. Môt công ty dự định chi không quá 900 triệu đồng để quảng cáo trên VTV1 với yêu cầu quảng cáo về số lần phát như sau: ít nhất 10 lần quảng cáo vào khoảng 20h30 và không quá 50 lần quảng cáo vào khung giờ 16h00-17h00.Gọi x, y lần luợt là số lần phát quảng cáo vào khoảng 20h30 và vào khung giờ 16h00-17h00.

Trong toán học, các điều kiện ràng buộc đối với x và y để đáp ứng nhu cầu trên của công ty đuợc thể hiện như thế nào?

Lời giải:

Gọi x, y lần luợt là số lần phát quảng cáo vào khoảng 20h30 và vào khung giờ 16h00-17h00. $(x,y\in \mathbb{N})$

Trong toán học, các điều kiện để đáp ứng nhu cầu trên của công ty đuợc thể hiện là:

+) ít nhất 10 lần quảng cáo vào khoảng 20h30: $x\ge 10$

+) không quá 50 lần quảng cáo vào khung giờ 16h00-17h00: $y\le 50$

+) chi không quá 900 triệu đồng: $30.x+6.y\le 900$

Luyện tập vận dụng 1 trang 25 Toán lớp 10: Chỉ ra một nghiệm của hệ bất phương trình sau: $\{\begin{array}{l}2x+y>0\\ x-3y<6\\ x-y\ge -4\end{array}$

Phương pháp giải:

Thay cặp số (1;1) vào 3 bất phương trình.

Lời giải:

Thay x=1; y=1 vào 3 bất phương trình ta được:

$2.1+1>0$ (Đúng)

$1-3.1<6$ (Đúng)

$1-1\ge -4$ (Đúng)

Vậy (1;1) là một nghiệm của hệ bất phương trình đã cho.

Hoạt động 1 trang 25 Toán lớp 10: Cho hệ bất phương trình sau:

$\{\begin{array}{l}x-y<3\left(1\right)\\ x+2y>-2\left(2\right)\end{array}$

a) Mỗi bát phương trình (1) và (2) có là bất phương trình bậc nhất hai ẩn không?

b) Chỉ ra một nghiệm chung của hai bất phương trình (1) và (2) trong hệ trên.

Thay x=1; y=1

Phương pháp giải:

a) Nhận diện bất phương trình bậc nhất hai ẩn.

b) Tìm cặp số (x;y) thỏa mãn đồng thời cả (1) và (2)

Lời giải:

a) Hai bất phương trình bài cho là bất phương trình bậc nhất hai ẩn.

b) Thay x=1;y=1 vào (1) ta được: 1-1<3(Luôn đúng)

Thay x=1; y=1 vào (2) ta được: 1+2.1>-2(Luôn đúng)

Giải Toán 10 trang 26 Tập 1

Hoạt động 2 trang 26 Toán lớp 10:  Cho hệ bất phương trình sau: $\{\begin{array}{l}x-2y\ge -2\\ 7x-4y\le 16\\ 2x+y\ge -4\end{array}$

a) Trong cùng mặt phẳng toạ độ Oxy, biểu diễn miền nghiệm của mỗi bất phương trình

trong hệ bất phương trình bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.

b) Tìm miền nghiệm của hệ bất phương trình đã cho.

Phương pháp giải:

a) Biểu diễn miền nghiệm của 3 bất phương trình trên cùng một mặt phẳng tọa độ.

b) Miền nghiệm của hệ là miền nghiệm chung của 3 bất phương trình.

Lời giải:

a) Trong cùng mặt phẳng toạ độ Oxy, vẽ ba đường thẳng:

$d_1:x-2y=-2$;

$d_2:7x-4y=16$

$d_3:2x+y=-4$

Thay tọa độ điểm O vào $x-2y$ ta được:

$0-2.0=0\ge -2$

=> Điểm O thuộc miền nghiệm

=> Gạch phần không chứa điểm O.

Thay tọa độ điểm O vào $7x-4y$ ta được:

$7.0-4.0=0\le 16$

=> Điểm O thuộc miền nghiệm

=> Gạch phần không chứa điểm O.

Thay tọa độ điểm O vào $2x+y$  ta được:

$2.0+0=0\ge -4$

=> Điểm O thuộc miền nghiệm

=> Gạch phần không chứa điểm O.

b)

 

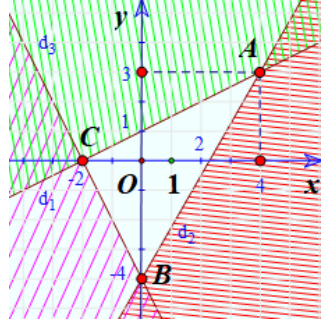
Miền nghiệm của hệ là phần không bị gạch bỏ chung của cả 3 miền nghiệm trên.

Chú ý:

Ở câu a, có thể thay điểm O bằng các điểm khác.

Giải Toán 10 trang 27 Tập 1

Luyện tập vận dụng 2 trang 27 Toán lớp 10: Biểu diễn miền nghiệm của hệ bất phương trình sau: $\{\begin{array}{l}3x-y>-3\\ -2x+3y<6\\ 2x+y>-4\end{array}$

Phương pháp giải:

Bước 1: Vẽ các đường thẳng.

Bước 2: Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.

Bước 3: Phần không bị gạch là miền nghiệm.

Lời giải:

Vẽ đường thẳng $3x-y=-3$ (nét đứt)

Thay tọa độ O vào $3x-y>-3$ ta được $3.0-0>-3$ (Đúng)

Gạch đi phần không chứa O

Vẽ đường thẳng $-2x+3y=6$ (nét đứt)

Thay tọa độ O vào $-2x+3y<6$ ta được $-2.0+3.0<6$ (Đúng)

Gạch đi phần không chứa O

Vẽ đường thẳng $2x+y=-4$(nét đứt)

Thay tọa độ O vào $2x+y>-4$ ta được $2.0+0>-4$ (Đúng)

Gạch đi phần không chứa O

Miền nghiệm của hệ là phần không bị gạch chéo:

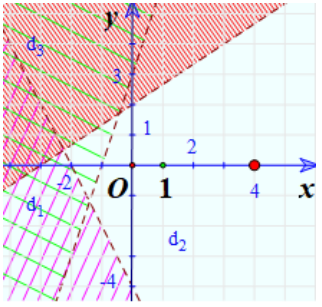
Giải Toán 10 trang 29 Tập 1

Bài 1 trang 29 Toán lớp 10: Kiểm tra xem mỗi cặp số (x;y) đã cho có là nghiệm của hệ bất phương trình tương ứng không.

a) $\{\begin{array}{l}3x+2y\ge -6\\ x+4y>4\end{array}$  $\left(0;2\right),\left(1;0\right)$

b) $\{\begin{array}{l}4x+y\le -3\\ -3x+5y\ge -12\end{array}$  $\left(-1;-3\right),\left(0;-3\right)$

Phương pháp giải:

– Thay từng cặp số vào mỗi hệ.

– Nếu thỏa mãn thì đó là nghiệm của hệ bất phương trình tương ứng.

Lời giải:

a) Thay $x=0,y=2$ vào hệ $\{\begin{array}{l}3x+2y\ge -6\\ x+4y>4\end{array}$ ta được:

$\{\begin{array}{l}3.0+2.2\ge -6\\ 0+4.2>4\end{array}$ (Đúng)

Thay $x=1,y=0$ vào hệ $\{\begin{array}{l}3x+2y\ge -6\\ x+4y>4\end{array}$ ta được:

$\{\begin{array}{l}3.1+2.0\ge -6\\ 1+4.0>4\left(Sai\right)\end{array}$

Vậy $\left(0;2\right)$ là nghiệm của hệ còn $\left(1;0\right)$ không là nghiệm.

b) Thay $x=-1,y=-3$ vào hệ $\{\begin{array}{l}4x+y\le -3\\ -3x+5y\ge -12\end{array}$ ta được:

$\{\begin{array}{l}4.\left(-1\right)+\left(-3\right)\le -3\\ -3\left(-1\right)+5.\left(-3\right)\ge -12\end{array}$$\iff \{\begin{array}{l}-7\le -3\\ -12\ge -12\end{array}$ (Đúng)

Thay $x=0,y=-3$ vào hệ $\{\begin{array}{l}4x+y\le -3\\ -3x+5y\ge -12\end{array}$ ta được:

$\{\begin{array}{l}4.0+\left(-3\right)\le -3\\ -3.0+5.\left(-3\right)\ge -12\end{array}$$\iff \{\begin{array}{l}-3\le -3\\ -15\ge -12\left(Sai\right)\end{array}$

Vậy $\left(-1;-3\right)$ là nghiệm của hệ còn $\left(0;-3\right)$ không là nghiệm.

Bài 2 trang 29 Toán lớp 10: Biểu diễn miền nghiệm của hệ bất phương trình:

a) $\{\begin{array}{l}x+2y<-4\\ y\ge x+5\end{array}$

b) $\{\begin{array}{l}4x-2y>8\\ x\ge 0\\ y\le 0\end{array}$

Phương pháp giải:

Bước 1: Vẽ các đường thẳng.

Bước 2: Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.

Bước 3: Phần không bị gạch là miền nghiệm.

Lời giải:

a) Vẽ các đường thẳng $x+2y=-4$(nét đứt) và $y=x+5$ (nét liền)

Thay tọa độ O vào $x+2y<-4$ ta được: $0+2.0<-4$ (Sai)

=> Gạch đi phần chứa O.

Thay tọa độ O vào $y\ge x+5$ ta được: $0\ge 0+5$ (Sai)

=> Gạch đi phần chứa O.

Miền nghiệm của hệ:

 

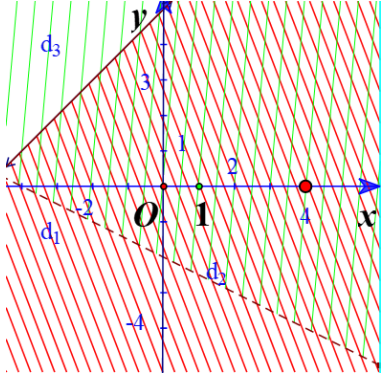
Từ hình vẽ ta thấy hệ vô nghiệm.

b) Vẽ các đường thẳng $4x-2y=8$(nét đứt) và hai trục (nét liền)

Thay tọa độ O vào $4x-2y>8$ ta được: $4.0-2.0>8$ (Sai)

=> Gạch đi phần chứa O.

Với $x\ge 0$ thì gạch phần bên trái Oy

Với $y\le 0$ thì gạch bên trên Ox

Miền nghiệm của hệ:

 

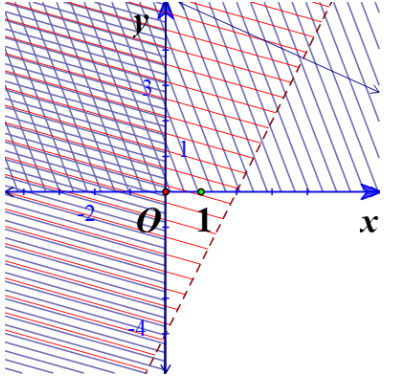
Bài 3 trang 29 Toán lớp 10: Miền không bị gạch ở mỗi Hình 12a, 12b là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?

 

 

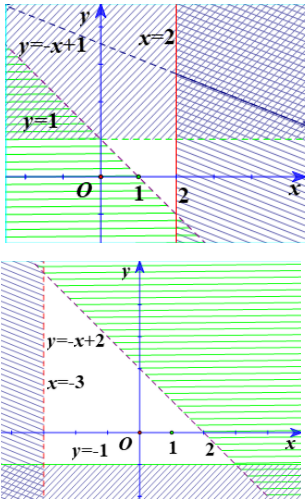
a) $\{\begin{array}{l}x+y<2\\ x>-3\\ y\ge -1\end{array}$

b) $\{\begin{array}{l}y<x\\ x\le 0\\ y>-3\end{array}$

c) $\{\begin{array}{l}y>-x+1\\ x\le 2\\ y<1\end{array}$

Phương pháp giải:

Xác định các đường thẳng dạng trên mỗi hình.

Với các đường thẳng x=a, nếu phần không bị gạch bên phải thì bất phương trình tương ứng là $x<a$ hoặc $x\le a$, ngược lại sẽ là $x>a$ hoặc $x\ge a$.

Với các đường thẳng y=b, nếu phần không bị gạch bên trên thì bất phương trình là $y>b$ hoặc $y\ge b$, ngược lại sẽ là $y<b$ hoặc $y\le b$.

Với các đường thẳng $y=ax+b$ cắt hai trục thì thay tọa độ điểm thuộc miền nghiệm vào, nếu vế trái nhỏ hơn vế phải thì bất phương trình là $y<ax+b$ hoặc $y\le ax+b$, ngược lại thì bất phương trình là $y>ax+b$ hoặc $y\ge ax+b$.

Lời giải:

Hình 12a

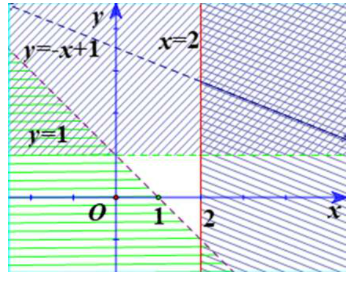
Ta thấy các đường thẳng trên hình là $y=1;x=2;y=-x+1$

Từ các phương trình trên thì ta chọn luôn là câu c mà không cần xét tiếp.

Hình 12b.

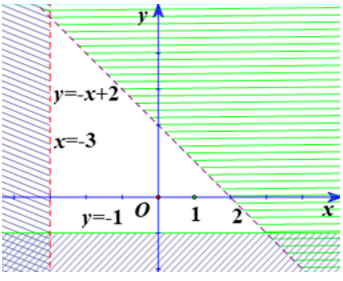
Ta thấy các đường thẳng trên hình là $y=-1;x=-3;x+y=-2$

Từ các phương trình trên thì ta chọn luôn là câu a mà không cần xét tiếp

Bài 4 trang 29 Toán lớp 10: Một phân xưởng sản xuất hai kiểu mũ. Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai. Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc. Phân xưởng làm việc 8 tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai. Tiền lãi khi bán một chiếc mũ kiểu thứ nhất là 24 nghìn đồng, một chiếc mũ kiểu thứ hai là 15 nghìn đồng. Tính số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất để tiền lãi thu được là cao nhất.

Phương pháp giải:

Bước 1: Gọi số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất lần lượt là $x$ và $y$ $\left(x,y\in \mathbb{N}\ast \right)$. Biểu diễn các đại lượng khác theo $x$ và $y$.

Bước 2: Lập hệ bất phương trình.

Bước 3: Biểu diễn miền nghiệm.

Bước 4: Tìm $x$ và $y$ để tiền lãi cao nhất.

Lời giải:

Bước 1: Gọi số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất lần lượt là $x$ và $y$ $\left(x,y\in \mathbb{N}\right)$. Biểu diễn các đại lượng khác theo $x$ và $y$.

Gọi số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất lần lượt là $x$ và $y$ $\left(x,y\in \mathbb{N}\right)$.

Theo giả thiết, thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai nên ta có $0\le x\le 200;0\le y\le 240$

Thời gian làm $y$ chiếc kiểu 2 trong một ngày là $\frac{y}{60}\left(h\right)$

Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai nên thời gian làm mũ thứ nhất là 1 giờ làm được 30 chiếc.

Thời gian làm $x$ chiếc kiểu 1 trong một ngày là $\frac{x}{30}\left(h\right)$

Tổng thời gian làm trong một ngày là 8h nên ta có:

$\frac{x}{30}+\frac{y}{60}=8$

Bước 2: Lập hệ bất phương trình.

Bước 3: Biểu diễn miền nghiệm.

Miền biểu diễn miền nghiệm là phần màu vàng:

 

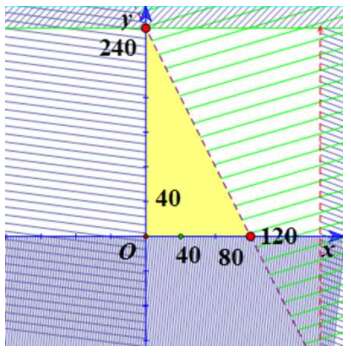
Bước 4: Tìm $x$ và $y$ để tiền lãi cao nhất.

Từ miền nghiệm ta thấy tiền lãi cao nhất tại khi điểm $\left(x;y\right)$ là một trong các đỉnh của tam giác màu vàng:

$T=24x+15y$

$T\left(0;240\right)=15.240=3600$ (nghìn đồng)

$T\left(120;0\right)=24.120=2880$(nghìn đồng)

Số lượng mũ kiểu 1 là 240 và số lượng mũ kiểu 2 là 0

Bài giảng Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn – Cánh diều

Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:

Bài 1: Bất phương trình bậc nhất hai ẩn

Bài tập cuối chương 2

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

====== ****&**** =====