Giải bài tập Toán lớp 10 Bài 4: Bất phương trình bậc hai một ẩn
Video giải Toán 10 Bài 4: Bất phương trình bậc hai một ẩn – Cánh diều
Giải Toán 10 trang 49 Tập 1
Câu hỏi khởi động trang 49 Toán lớp 10: Bác Dũng muốn uốn tấm tôn phẳng có dạng hình chữ nhật với bề ngang 32 cm thành một rãnh dẫn nước bằng cách chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông (Hình 25). Để đảm bảo kī thuật, diện tích mặt cắt ngang của rānh dẫn nước phải lớn hơn hoặc bằng 120 . Rãnh dẫn nước phải có độ cao ít nhất là bao nhiêu xǎng-ti-mét?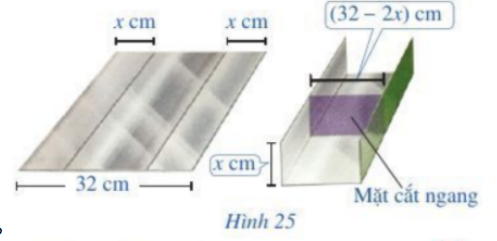
Phương pháp giải:
Diện tích mặt cắt:
Yêu cầu kĩ thuật:
Lời giải:
Mặt cắt ngang là hình chữ nhật với chiều dài là 32 – 2x và chiều rộng là x (cm).
Diện tích mặt cắt là:
Để đảm bảo yêu cầu kĩ thuật thì :
Tam thức bậc hai có hai nghiệm là và có hệ số
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho tam thức mang dấu “-” là
Tức là rãnh nước phải có độ cao lớn hơn 6cm và nhỏ hơn 10cm.
I. Bất phương trình bậc hai một ẩn
Hoạt động 1 trang 49 Toán lớp 10: Quan sát và nêu đặc điểm của biểu thức ở vế trái của bất phương trình
Phương pháp giải:
Nhận xét bậc và hệ số của
Lời giải:
Vế trái của bất phương trình là đa thức bậc 2 và có hệ số cao nhất là 3>0
Luyện tập vận dụng 1 trang 49 Toán lớp 10: a) Cho hai ví dụ về bất phương trình bậc hai một ẩn.
b) Cho hai ví dụ về bất phương trình mà không phải là bất phương trình bậc hai một ẩn.
Phương pháp giải:
a) Lấy ví dụ
b) Có thể lấy bất phương trình bậc nhất hoặc bất phương trình chứa 2 ẩn.
Lời giải:
a) Ví dụ:
b) Bất phương trình bậc nhất:
Bất phương trình hai ẩn:
II. Giải bất phương trình bậc hai một ẩn
Giải Toán 10 trang 50 Tập 1
Hoạt động 2 trang 50 Toán lớp 10: a) Lập bảng xét dấu của tam thức bậc hai
b) Giải bất phương trình
Phương pháp giải:
a) Tìm nghiệm của phương trình , xét hệ số và lập bảng xét dấu.
b) Dựa vào bảng xét dấu, lấy các khoảng để
Lời giải:
a) Ta có tam thức bậc hai có 2 nghiệm phân biệt và hệ số
Ta có bảng xét dấu f(x) như sau:

Vậy tập nghiệm của bất phương trình là b) Từ bảng xét dấu ta thấy
Luyện tập vận dụng 2 trang 50 Toán lớp 10: Giải các bất phương trình bậc hai sau:
a)
b)
Phương pháp giải:
Giải bất phương trình dạng .
Bước 1: Xác định dấu của hệ số a và tìm nghiệm của (nếu có)
Bước 2: Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị của x sao cho mang dấu “+”
Bước 3: Các bất phương trình bậc hai có dạng được giải bằng cách tương tự.
Lời giải:
a) Ta có và tam thức bậc hai có
=> vô nghiệm.
=>
b) Ta có: và
=> có nghiệm duy nhất .
=>
Hoạt động 3 trang 50 Toán lớp 10: Cho bất phương trình .
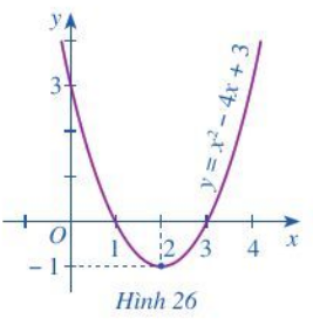
Quan sát parabol ở Hình 26 và cho biết:
a) Bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía nào của trục hoành.
b) Phần parabol (P) nằm phía trên trục hoành ứng với những giá trị nào của x.
Phương pháp giải:
– Nếu dấu bất phương trình dương thì bất phương trình biểu diễn phần (P) phía trên trục hoành và ngược lại.
Lời giải:
a) Từ đồ thị ta thấy bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía trên trục hoành.
b) Phần parabol (P) nằm phía trên trục hoành ứng với các giá trị của x thuộc
Giải Toán 10 trang 51 Tập 1
Luyện tập vận dụng 3 trang 51 Toán lớp 10: Giải mỗi bất phương trình bậc hai sau bằng cách sử dụng đồ thị:
a)
b)
Phương pháp giải:
Bước 1: Vẽ đồ thị biểu diễn các hàm số.
Bước 2: Quan sát đồ thị và lấy các giá trị tương ứng với bất phương trình.
Lời giải:
a) Ta có đồ thị:
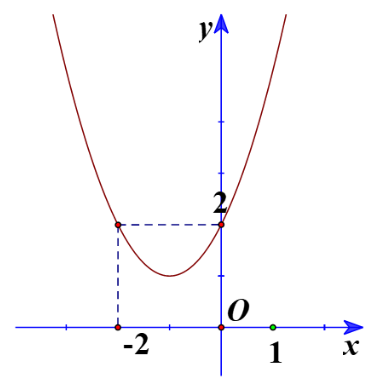
Từ đồ thị ta thấy biểu diễn phần parabol nằm phía trên trục hoành, tương ứng với mọi .
Vậy tập nghiệm của bất phương trình là .
b) Ta có đồ thị:
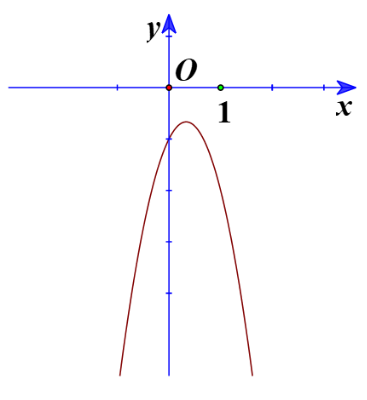
Từ đồ thị ta thấy biểu diễn phần parabol nằm phía trên trục hoành, tương ứng với
Vậy tập nghiệm của bất phương trình là .
III. Ứng dụng của bất phương trình bậc hai một ẩn
Giải Toán 10 trang 53 Tập 1
Luyện tập vận dụng 4 trang 53 Toán lớp 10: Tổng chi phí T (đơn vị tính: nghìn đồng) để sản xuất Q sản phẩm được cho bởi biểu thức ; giá bán của 1 sản phẩm là 170 nghìn đồng. Số sản phẩm được sản xuất trong khoảng nào để đảm bảo không bị lỗ (giả thiết các sản phẩm được bán hết)?
Phương pháp giải:
Biểu diễn số tiền khi bán Q sản phẩm.
Lợi nhuận=Doanh thu-chi phí.
Để không bị lỗ thì lợi nhuân phải lớn hơn hoặc bằng 0.
Lời giải:
Doanh thu khi bán Q sản phẩm là 170Q nghìn đồng.
Lợi nhuận khi bán Q sản phẩm là (nghìn đồng)
Để không bị lỗ thì
có 2 nghiệm phân biệt
(1)
Vậy để không bị lỗ thì số sản phẩm được sản suất phải nằm trong khoảng từ 30 đến 110 sản phẩm.
Bài tập
Giải Toán 10 trang 54 Tập 1
Bài 1 trang 54 Toán lớp 10: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc hai một ẩn? Vì sao?
a)
b)
c)
Phương pháp giải:
– Xác định bậc của bất phương trình.
– Xác định số ẩn của bất phương trình.
Lời giải:
a) không là bất phương trình bậc hai một ẩn vì bậc của bất phương trình này là bậc 1.
b) là bất phương trình bậc hai một ẩn vì bậc của bất phương trình này là bậc 2 và có đúng 1 ẩn là y.
c) không là bất phương trình bậc hai một ẩn vì có 2 ẩn là x và y.
Bài 2 trang 54 Toán lớp 10: Dựa vào đồ thị hàm số bậc hai trong mỗi Hình 30a, 30b, 30c, hãy viết tập nghiệm của mỗi bất phương trình sau: .
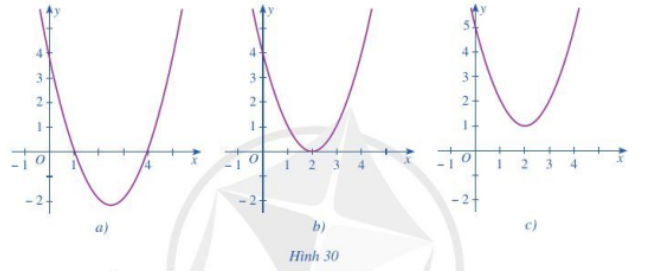
Phương pháp giải:
– Quan sát đồ thị.
– Phần phía trên trục hoành biểu diễn tập nghiệm của bất phương trình (không tính giao điểm với đồ thị)
– Phần phía dưới trục hoành biểu diễn tập nghiệm của bất phương trình (không tính giao điểm với đồ thị)
Lời giải:
Hình 30a:
có tập nghiệm là
có tập nghiệm là
có tập nghiệm là
có tập nghiệm là
Hình 30b:
có tập nghiệm là
có tập nghiệm là
có tập nghiệm là
có tập nghiệm là
Hình 30c:
có tập nghiệm là
có tập nghiệm là
có tập nghiệm là
có tập nghiệm là
Bài 3 trang 54 Toán lớp 10: Giải các bất phương trình bậc hai sau:
a)
b)
c)
d)
Phương pháp giải:
Giải bất phương trình dạng .
Bước 1: Xác định dấu của hệ số a và tìm nghiệm của (nếu có)
Bước 2: Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị của x sao cho mang dấu “+”
Bước 3: Các bất phương trình bậc hai có dạng được giải bằng cách tương tự.
Lời giải:
a) Ta có và
=> có 2 nghiệm phân biệt .
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho mang dấu “+” là
Vậy tập nghiệm của bất phương trình là
b) Ta có và
=> có 2 nghiệm phân biệt .
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho mang dấu “-” là
Vậy tập nghiệm của bất phương trình là
c) Ta có và
=> có nghiệm duy nhất .
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho mang dấu “-” là
Vậy tập nghiệm của bất phương trình là
d)
Ta có và
=> có 2 nghiệm phân biệt .
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho mang dấu “+” là
Vậy tập nghiệm của bất phương trình là
Bài 4 trang 54 Toán lớp 10: Tìm m để phương trình có nghiệm.
Phương pháp giải:
Phương trình có nghiệm khi và chỉ khi .
Lời giải:
Ta có ,
Phương trình có nghiệm khi và chỉ khi
Vậy phương trình có nghiệm với mọi số thực m.
Bài 5 trang 54 Toán lớp 10: Xét hệ toạ độ Oth trên mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng giây) và trục Oh biểu thị độ cao h (tính bằng mét). Một quả bóng được đá lên từ điểm A(0; 0,2) và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8,5 m sau 1 giây và đạt độ cao 6 m sau 2 giây.
a) Hãy tìm hàm số bậc hai biểu thị quỹ đạo chuyển động của quả bóng.
b) Trong khoảng thời gian nào thì quả bóng vẫn chưa chạm đất?
Phương pháp giải:
a) Đặt phương trình parabol là
Thay tọa độ điểm A, điểm (1;8,5) và điểm (2;6) vào tìm a, b và c.
b) Tìm t để h>0
Lời giải:
a) Đặt phương trình parabol là
Ta có quả bóng được đá lên từ điểm A(0; 0,2) nên
Ta có quả bóng đạt độ cao 8,5 m sau 1 giây có nghĩa là tại t=1 thì h=8,5. Khi đó
(1)
Ta có quả bóng đạt độ cao 6 m sau 2 giây có nghĩa là tại t=2 thì h=6.
=>
Từ (1) và (2) ta được hệ
Vậy
b) Để quả bóng không chạm đất thì
Vậy trong khoảng thời gian từ lúc đá đến thời gian thì quả bóng chưa chạm đất.
Bài 6 trang 54 Toán lớp 10: Công ty An Bình thông báo giá tiền cho chuyến đi tham quan của một nhóm khách du lịch như sau:
10 khách đầu tiên có giá là 800 000 đồng/người. Nếu có nhiều hơn 10 người đăng kí thì cứ có thêm 1 người, giá vé sẽ giảm 10 000 đồng/người cho toàn bộ hành khách.
a) Gọi x là số lượng khách từ người thứ 11 trở lên của nhóm. Biểu thị doanh thu theo x.
b) Số người của nhóm khách du lịch nhiều nhất là bao nhiêu thì công ty không bị lỗ? Biết rằng chi phí thực sự cho chuyến đi là 700 000 đồng/người.
Phương pháp giải:
a) Biểu diễn giá vé khi có thêm x khách
b) Tính chi phí thực sau khi thêm x vị khách. Tìm số người nhiều nhất để công ty không bị lỗ.
Lời giải:
a) Gọi x là số lượng khách từ người thứ 11 trở lên của nhóm (x>0)
Giá vé khi có thêm x khách là: (đồng/người)
Doanh thu khi thêm x khách là:
(đồng)
b) Chi phí thực sau khi thêm x vị khách là: 700 000(x+10) (đồng)
Lợi nhuận khi thêm x vị khách là:
Để công ty không bị lỗ thì lợi nhuận lớn hơn hoặc bằng 0
Khi đó số khách du lịch tối đa là người thì công ty không bị lỗ.
Bài giảng Toán 10 Bài 4: Bất phương trình bậc hai một ẩn – Cánh diều
Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:
Bài 3: Dấu của tam thức bậc hai
Bài 5: Hai dạng phương trình quy về phương trình bậc hai
Bài tập cuối chương 3
Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác
====== ****&**** =====