Giải Toán 12 Bài 2: Tích phân

Giải bài tập Toán lớp 12 Bài 2: Tích phân

Trả lời câu hỏi giữa bài

Trả lời câu hỏi 1 trang 101 SGK Giải tích 12: Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng $y=2x+1$, trục hoành và hai đường thẳng $x=1,x=t$ $(1\le t\le 5)$ (H.45).

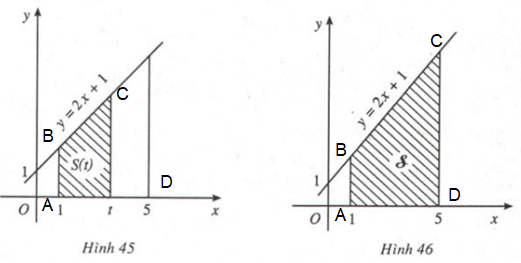
a) Tính diện tích $S$ của hình $T$ khi $t=5$ (H.46).

b) Tính diện tích $S(t)$ của hình $T$ khi $x\in [1;5]$

c) Chứng minh rằng $S(t)$ là một nguyên hàm của $f(t)=2t+1,t\in [1;5]$ và diện tích $S=S(5)-S(1)$.

Phương pháp giải:

Dựa vào công thức tính diện tích hình thang $ABCD(AB//CD)$ là:$S=\frac{\left(AB+CD\right).h}{2}$

Lời giải:

a)

(Hình 46)

Kí hiệu $A$ là điểm có tọa độ $(1,0),D$ là điểm có tọa độ $(5,0)$. $B,C$ lần lượt là giao điểm của đường thẳng $x=1$ và $x=5$ với đường thẳng $y=2x+1$.

– Khi đó $B$ và $C$ sẽ có tọa độ lần lượt là $(1,3)$ và $(5,11)$.

– Ta có: $AB=3,CD=11,AD=4$. Diện tích hình thang:

$ABCD=\frac{(AB+CD).AD}{2}=28$

b)

Kí hiệu $A$ là điểm có tọa độ $(1,0)$, $D$ là điểm có tọa độ $(t,0)$. B, C\) lần lượt là giao điểm của đường thẳng $x=1$ và $x=t$ với đường thẳng $y=2x+1$.

– Khi đó ta có $B(1,3)$ và $C(t,2t+1)$.

– Ta có $AB=3,AD=t–1,CD=2t+1$.

– Khi đó diện tích hình thang:

$S(t)=\frac{(AB+CD).AD}{2}$ $=\frac{(3+2t+1).(t-1)}{2}$ $=t^2+t-2$

Do đó $S(t)=t^2+t-2$

c)

Vì $S^{\prime }(t)=(t^2+t-2{)}^{\prime }$ $=2t+1$ nên hàm số $S(t)$ là một nguyên hàm của hàm số $f(t)=2t+1,t\in [1;5]$.

Dễ thấy $S(5)-S(1)$ $=\left(5^2+5-2\right)-\left(1^2+1-2\right)$ $=28=S$ hay $S=S(5)-S(1)$.

Trả lời câu hỏi 2 trang 104 SGK Giải tích 12: Giả sử $f(x)$ là hàm số liên tục trên đoạn $[a;b],F(x)$ và $G(x)$ là hai nguyên hàm của $f(x)$. Chứng minh rằng $F(b)–F(a)=G(b)–G(a)$, (tức là hiệu số $F(b)–F(a)$ không phụ thuộc việc chọn nguyên hàm).

Lời giải:

– Vì $F(x)$ và $G(x)$ đều là nguyên hàm của $f(x)$ nên tồn tại một hằng số $C$ sao cho: $F(x)=G(x)+C$

– Khi đó $F(b)–F(a)=G(b)+C–G(a)–C=G(b)–G(a)$.

Trả lời câu hỏi 3 trang 106 SGK Giải tích 12: Hãy chứng minh các tính chất 1 và 2.

Lời giải:

Tính chất 1:

+) Nếu $k=0$ thì tính chất đúng.

+) Nếu $k\ne 0$ thì $\int kf\left(x\right)dx=k\int f\left(x\right)dx=F\left(x\right)$ $\Rightarrow \int f\left(x\right)dx=\frac{F\left(x\right)}{k}$

Do đó $\underset{a}{\overset{b}{\int }}kf\left(x\right)dx={F\left(x\right)|}_a^b=F\left(b\right)-F\left(a\right)$ và $k\underset{a}{\overset{b}{\int }}f\left(x\right)dx=k.{\frac{F\left(x\right)}{k}|}_a^b$ $=F\left(b\right)-F\left(a\right)$

Từ đó suy ra $\underset{a}{\overset{b}{\int }}kf\left(x\right)dx=k\underset{a}{\overset{b}{\int }}f\left(x\right)dx$.

Tính chất 2:

Giả sử $F\left(x\right),G\left(x\right)$ lần lượt là các nguyên hàm của hai hàm số $f\left(x\right),g\left(x\right)$.

Ta có: $\int \left[f\left(x\right)\pm g\left(x\right)\right]dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx$ $=F\left(x\right)\pm G\left(x\right)$

Khi đó $\underset{a}{\overset{b}{\int }}\left[f\left(x\right)\pm g\left(x\right)\right]dx={\left[F\left(x\right)\pm G\left(x\right)\right]|}_a^b$ $=\left[F\left(b\right)\pm G\left(b\right)\right]-\left[F\left(a\right)\pm G\left(a\right)\right]$ $=\left[F\left(b\right)-F\left(a\right)\right]\pm \left[G\left(b\right)-G\left(a\right)\right]$.

Lại có $\underset{a}{\overset{b}{\int }}f\left(x\right)dx\pm \underset{a}{\overset{b}{\int }}g\left(x\right)dx$ $={F\left(x\right)|}_a^b\pm {G\left(x\right)|}_a^b$ $=\left[F\left(b\right)-F\left(a\right)\right]\pm \left[G\left(b\right)-G\left(a\right)\right]$.

Từ đó ta có điều phải chứng minh.

Trả lời câu hỏi 4 trang 108 SGK Giải tích 12: Cho tích phân $I=\underset{0}{\overset{1}{\int }}{(2x+1)}^{2}dx$

a) Tính $I$ bằng cách khai triển ${\left(2x+1\right)}^2$

b) Đặt $u=2x+1$. Biến đổi biểu thức ${\left(2x+1\right)}^{2}dx$ thành $g(u)du$.

c) Tính $\underset{u(0)}{\overset{u(1)}{\int }}g(u)du$ và so sánh kết quả với $I$ trong câu 1.

Lời giải:

a)

$\begin{array}{rl}& I=\underset{0}{\overset{1}{\int }}{(2x+1)}^{2}dx=\underset{0}{\overset{1}{\int }}\left(4x^2+4x+1\right)dx\\ & =(\frac{4}{3}{x}^3+2x^2+x){|}_0^1=\frac{13}{3}\end{array}$

b)

Vì $u=2x+1$ nên $du=2dx$. Ta có:

$(2x+1{)}^{2}dx=u^2\frac{du}{2}$

c)

$u(1)=3;u(0)=1$. Ta có:

$\underset{u(0)}{\overset{u(1)}{\int }}g(u)du=\underset{1}{\overset{3}{\int }}{u}^2\frac{du}{2}=\frac{u^3}{6}{|}_1^3=\frac{13}{3}$

Vậy $I=\frac{13}{3}$

Trả lời câu hỏi 5 trang 110 SGK Giải tích 12: a) Hãy tính $\int \left(x+1\right)e^{x}dx$ bằng phương pháp tính nguyên hàm từng phần.

b) Từ đó tính $\underset{0}{\overset{1}{\int }}(x+1)e^{x}dx$

Lời giải:

a)

Đặt $\{\begin{array}{l}u=x+1\\ dv=e^{x}dx\end{array}\Rightarrow \{\begin{array}{l}du=dx\\ v=e^x\end{array}$ $\Rightarrow \int \left(x+1\right)e^{x}dx=\left(x+1\right)e^x-\int e^{x}dx$ $=\left(x+1\right)e^x-e^x+C$ $=x{e}^x+C$

b)

Vì $F(x)=x{e}^x$ là một nguyên hàm của hàm số $f(x)=(x+1)e^x$ nên

$\underset{0}{\overset{1}{\int }}\left(x+1\right)e^{x}dx={x{e}^x|}_0^1$ $=1.e^1-0.e^0=e$

Câu hỏi và bài tập (trang 112, 113 SGK Giải tích 12)
Bài 1 trang 112 SGK Giải tích 12:Tính các tích phân sau:

a) ${\int }_{\frac{-1}{2}}^{\frac{1}{2}}\sqrt[3]{(1-x{)}^2}dx$

b) ${\int }_0^{\frac{\pi }{2}}sin(\frac{\pi }{4}-x)dx$

c) ${\int }_{\frac{1}{2}}^2\frac{1}{x(x+1)}dx$

d) ${\int }_0^{2}x(x+1{)}^{2}dx$

e) ${\int }_{\frac{1}{2}}^2\frac{1-3x}{(x+1{)}^2}dx$

g) ${\int }_{\frac{-\pi }{2}}^{\frac{\pi }{2}}sin3xcos5xdx$

Phương pháp giải:

a) Sử dụng công thức nguyên hàm mở rộng $\underset{}{\overset{}{\int }}{\left(ax+b\right)}^{n}dx=\frac{1}{a}\frac{{\left(ax+b\right)}^{n+1}}{n+1}+C$

b) Sử dụng công thức nguyên hàm mở rộng:

$\underset{}{\overset{}{\int }}\sin \left(ax+b\right)dx$$=-\frac{1}{a}\cos \left(ax+b\right)+C$

c) Sử dụng phân tích: $\frac{1}{x\left(x+1\right)}=\frac{1}{x}-\frac{1}{x+1}$ sau đó sử dụng công thức tính nguyên hàm mở rộng: $\underset{}{\overset{}{\int }}\frac{1}{ax+b}dx=\frac{1}{a}.\ln \left|ax+b\right|+C$.

d) Nhân đa thức và áp dụng công thức nguyên hàm: $\underset{}{\overset{}{\int }}{x}^{n}dx=\frac{x^{n+1}}{n+1}+C$.

e) Phân tích đa thức trong tích phân dưới dạng : $\frac{1-3x}{{\left(x+1\right)}^2}=\frac{A}{x+1}+\frac{B}{{\left(x+1\right)}^2}$ và sử dụng các công thức nguyên hàm:

$\underset{}{\overset{}{\int }}\frac{dx}{ax+b}=\frac{1}{a}\ln \left|ax+b\right|+C$

$\underset{}{\overset{}{\int }}\frac{dx}{{\left(ax+b\right)}^2}=\frac{1}{a}\frac{-1}{ax+b}+C$

g) Cách 1: Chứng minh hàm số $f\left(x\right)=\sin 3x\cos 5x$ là hàm số lẻ và áp dụng công thức $\underset{-a}{\overset{a}{\int }}f\left(x\right)dx=0$ (Với f(x) là hàm số lẻ, $a\in R$.

Cách 2: Sử dụng công thức biến đổi tích thành tổng.

Lời giải:

a)

$\begin{array}{l}\underset{-\frac{1}{2}}{\overset{\frac{1}{2}}{\int }}\sqrt[3]{{\left(1-x\right)}^2}dx=\underset{-\frac{1}{2}}{\overset{\frac{1}{2}}{\int }}{\left(1-x\right)}^{\frac{2}{3}}dx\\ ={\frac{1}{-1}.\frac{{\left(1-x\right)}^{\frac{2}{3}+1}}{\frac{2}{3}+1}|}_{-\frac{1}{2}}^{\frac{1}{2}}\\ ={-1.\frac{{\left(1-x\right)}^{\frac{5}{3}}}{\frac{5}{3}}|}_{-\frac{1}{2}}^{\frac{1}{2}}\\ ={-\frac{3}{5}{\left(1-x\right)}^{\frac{5}{3}}|}_{-\frac{1}{2}}^{\frac{1}{2}}\\ =-\frac{3}{5}.\left[{\left(\frac{1}{2}\right)}^{\frac{5}{3}}-{\left(\frac{3}{2}\right)}^{\frac{5}{3}}\right]\\ =-\frac{3}{5}\left[\frac{1}{\sqrt[3]{2^5}}-\frac{\sqrt[3]{3^5}}{\sqrt[3]{2^5}}\right]\\ =-\frac{3}{5}\left[\frac{1}{\sqrt[3]{2^3{.2}^2}}-\frac{\sqrt[3]{3^3{.3}^2}}{\sqrt[3]{2^3{.2}^2}}\right]\\ =-\frac{3}{5}\left[\frac{1}{2\sqrt[3]{4}}-\frac{3\sqrt[3]{9}}{2\sqrt[3]{4}}\right]\\ =\frac{3}{10\sqrt[3]{4}}\left(3\sqrt[3]{9}-1\right)\end{array}$

b)

$\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sin \left(\frac{\pi }{4}-x\right)dx$

$=-\frac{1}{-1}{\cos \left(\frac{\pi }{4}-x\right)|}_0^{\frac{\pi }{2}}$

$={\cos \left(\frac{\pi }{4}-x\right)|}_0^{\frac{\pi }{2}}$

$=\cos \left(-\frac{\pi }{4}\right)-\cos \frac{\pi }{4}=0$

c)

Ta có: $\frac{1}{x\left(x+1\right)}$

$=\frac{x+1-x}{x\left(x+1\right)}=\frac{x+1}{x\left(x+1\right)}-\frac{x}{x\left(x+1\right)}$

$=\frac{1}{x}-\frac{1}{x+1}$

$\begin{array}{l}\Rightarrow \underset{\frac{1}{2}}{\overset{2}{\int }}\frac{1}{x\left(x+1\right)}dx=\underset{\frac{1}{2}}{\overset{2}{\int }}\left(\frac{1}{x}-\frac{1}{x+1}\right)dx\\ ={\left(\ln \left|x\right|-\ln \left|x+1\right|\right)|}_{\frac{1}{2}}^2={\ln \left|\frac{x}{x+1}\right||}_{\frac{1}{2}}^2\\ =\ln \frac{2}{3}-\ln \frac{1}{3}=\ln \left(\frac{2}{3}:\frac{1}{3}\right)=\ln 2\end{array}$.

d)

$\begin{array}{l}x{\left(x+1\right)}^2=x\left(x^2+2x+1\right)\\ =x^3+2x^2+x\\ \Rightarrow \underset{0}{\overset{2}{\int }}x{\left(x+1\right)}^{2}dx\\ =\underset{0}{\overset{2}{\int }}\left(x^3+2x^2+x\right)dx\\ ={\left(\frac{x^4}{4}+2\frac{x^3}{3}+\frac{x^2}{2}\right)|}_0^2\\ =\left(\frac{2^4}{4}+2.\frac{2^3}{3}+\frac{2^2}{2}\right)-0\\ =\frac{34}{3}\end{array}$

e)

$\begin{array}{l}\frac{1-3x}{{\left(x+1\right)}^2}=\frac{-3x-3+4}{{\left(x+1\right)}^2}\\ =\frac{-3\left(x+1\right)+4}{{\left(x+1\right)}^2}=-\frac{3}{x+1}+\frac{4}{{\left(x+1\right)}^2}\\ \Rightarrow \underset{\frac{1}{2}}{\overset{2}{\int }}\frac{1-3x}{{\left(x+1\right)}^2}dx\\ =\underset{\frac{1}{2}}{\overset{2}{\int }}\left(-\frac{3}{x+1}+\frac{4}{{\left(x+1\right)}^2}\right)dx\\ =-3\underset{\frac{1}{2}}{\overset{2}{\int }}\frac{dx}{x+1}+4\underset{\frac{1}{2}}{\overset{2}{\int }}\frac{dx}{{\left(x+1\right)}^2}\\ =-{3\ln \left|x+1\right||}_{\frac{1}{2}}^2-{\frac{4}{x+1}|}_{\frac{1}{2}}^2\\ =-3\left(\ln 3-\ln \frac{3}{2}\right)-4\left(\frac{1}{3}-\frac{2}{3}\right)\\ =-3\ln 2+\frac{4}{3}\end{array}$

g)

Cách 1:

Đặt $f(x)=sin3xcos5x$ ta có:

$f\left(-x\right)=\sin \left(-3x\right)\cos \left(-5x\right)$$=-\sin 3x\cos 5x=-f\left(x\right)$

$\Rightarrow$ hàm số đã cho là hàm số lẻ, từ đó ta có:

$\underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}\sin 3x\cos 5xdx=0$.

Cách 2:

$\begin{array}{l}\sin 3x\cos 5x\\ =\frac{1}{2}\left[\sin \left(3x+5x\right)+\sin \left(3x-5x\right)\right]\\ =\frac{1}{2}\left(\sin 8x+\sin \left(-2x\right)\right)\\ =\frac{1}{2}\left(\sin 8x-\sin 2x\right)\\ \Rightarrow \underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}\sin 3x\cos 5xdx\\ =\frac{1}{2}\underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}\left(\sin 8x-\sin 2x\right)dx\\ =\frac{1}{2}{\left(-\frac{\cos 8x}{8}+\frac{\cos 2x}{2}\right)|}_{-\frac{\pi }{2}}^{\frac{\pi }{2}}\\ =\frac{1}{2}\left(-\frac{5}{8}-\left(-\frac{5}{8}\right)\right)=0\end{array}$

Bài 2 trang 112 SGK Giải tích 12: Tính các tích phân sau:

a) ${\int }_0^2\left|1-x\right|dx$

b) ${\int }_0^{\frac{\pi }{2}}{\sin }^{2}xdx$

c) ${\int }_0^{\ln 2}\frac{e^{2x+1}+1}{e^x}dx$

d) ${\int }_0^{\pi }\sin 2x{\cos }^{2}xdx$

Phương pháp giải:

a) Phá dấu giá trị tuyệt đối.

b) Sử dụng công thức hạ bậc: ${\sin }^{2}x=\frac{1-\cos 2x}{2}$

c) Chia tử cho mẫu và sử dụng công thức: $\underset{}{\overset{}{\int }}{e}^{ax+b}dx=\frac{1}{a}{e}^{ax+b}+C$
d) Sử dụng công thức hạ bậc: ${\cos }^{2}x=\frac{1+\cos 2x}{2}$.

Lời giải:

a)

Ta có: $\left|1-x\right|=[\begin{array}{l}1-xkhix\le 1\\ x-1khix>1\end{array}$

$\Rightarrow {\int }_0^2\left|1-x\right|dx={\int }_0^1\left|1-x\right|dx+{\int }_1^2\left|1-x\right|dx$

$={\int }_0^1(1-x)dx+{\int }_1^2(x-1)dx$

$={\left(x-\frac{x^2}{2}\right)|}_0^1+{\left(\frac{x^2}{2}-x\right)|}_1^2=\frac{1}{2}+\frac{1}{2}=1$

b)

$\begin{array}{l}\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\sin }^{2}xdx=\frac{1}{2}\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(1-\cos 2x\right)dx\\ =\frac{1}{2}{\left(x-\frac{\sin 2x}{2}\right)|}_0^{\frac{\pi }{2}}\\ =\frac{1}{2}.\frac{\pi }{2}=\frac{\pi }{4}\end{array}$

c)

$\begin{array}{l}\underset{0}{\overset{\ln 2}{\int }}\frac{e^{2x+1}+1}{e^x}dx=\underset{0}{\overset{\ln 2}{\int }}\left(e^{2x+1-x}+e^{-x}\right)dx\\ =\underset{0}{\overset{\ln 2}{\int }}\left(e^{x+1}+e^{-x}\right)dx\\ ={\left(e^{x+1}-e^{-x}\right)|}_0^{\ln 2}\\ =e^{\ln 2+1}-e^{-\ln 2}-\left(e-1\right)\end{array}$

$\begin{array}{l}=e^{\ln 2}.e^1-{\left(e^{\ln 2}\right)}^{-1}-e+1\\ =2.e-2^{-1}-e+1\\ =2e-\frac{1}{2}-e+1\\ =e+\frac{1}{2}\end{array}$

d)

$\begin{array}{l}\sin 2x{\cos }^{2}x=\sin 2x\frac{1+\cos 2x}{2}\\ =\frac{1}{2}\sin 2x+\frac{1}{2}\sin 2x\cos 2x=\frac{1}{2}\sin 2x+\frac{1}{4}\sin 4x\\ \Rightarrow \underset{0}{\overset{\pi }{\int }}\sin 2x{\cos }^{2}xdx=\underset{0}{\overset{\pi }{\int }}\left(\frac{1}{2}\sin 2x+\frac{1}{4}\sin 4x\right)dx\\ ={\left(-\frac{1}{4}\cos 2x-\frac{1}{16}\cos 4x\right)|}_0^{\pi }\\ =-\frac{1}{4}-\frac{1}{16}-\left(-\frac{1}{4}-\frac{1}{16}\right)=0\end{array}$

Bài 3 trang 113 SGK Giải tích 12: Sử dụng phương pháp đổi biến số, tính tích phân:

a) ${\int }_0^3\frac{x^2}{(1+x{)}^{\frac{3}{2}}}dx$ (Đặt $u=x+1$) 

b) ${\int }_0^1\sqrt{1-x^2}dx$ (Đặt $x=sint$ )

c) ${\int }_0^1\frac{e^x(1+x)}{1+x.e^x}dx$ (Đặt $u=1+x.e^x$)

d) ${\int }_0^{\frac{a}{2}}\frac{1}{\sqrt{a^2-x^2}}dx$ (Đặt $x=asint$)

Phương pháp giải:

a) Đặt $u=x+1$ và sử dụng công thức nguyên hàm cỏ bản:

$\int x^{\alpha }dx=\frac{x^{\alpha +1}}{\alpha +1}+C\left(\alpha \ne -1\right)$

b) Đặt $x=sint$

Sử dụng công thức hạ bậc: ${\cos }^2\alpha =\frac{1+\cos 2\alpha }{2}$

Sử dụng công thức nguyên hàm: $\int \cos \left(ax+b\right)dx=\frac{\sin \left(ax+b\right)}{a}+C$

c) Đặt $u=1+x.e^x$.
d) Đặt $x=asint$.

Lời giải:

a)

Đặt $u=x+1\Rightarrow du=dx$ và $x=u-1$.

Đổi cận: $\{\begin{array}{l}x=0\Rightarrow u=1\\ x=3\Rightarrow u=4\end{array}$

$\begin{array}{l}\underset{0}{\overset{3}{\int }}\frac{x^2}{{\left(1+x\right)}^{\frac{3}{2}}}dx=\underset{1}{\overset{4}{\int }}\frac{{\left(u-1\right)}^2}{u^{\frac{3}{2}}}du\\ =\underset{1}{\overset{4}{\int }}\frac{u^2-2u+1}{u^{\frac{3}{2}}}du\\ =\underset{1}{\overset{4}{\int }}\left(u^{\frac{1}{2}}-2u^{-\frac{1}{2}}+u^{-\frac{3}{2}}\right)du\\ ={\left(\frac{u^{\frac{1}{2}+1}}{\frac{1}{2}+1}-2.\frac{u^{-\frac{1}{2}+1}}{-\frac{1}{2}+1}+\frac{u^{-\frac{3}{2}+1}}{-\frac{3}{2}+1}\right)|}_1^4\\ ={\left(\frac{2}{3}{u}^{\frac{3}{2}}-4u^{\frac{1}{2}}-2u^{-\frac{1}{2}}\right)|}_1^4\\ =-\frac{11}{3}-\left(-\frac{16}{3}\right)=\frac{5}{3}\end{array}$

b)

Đặt $x=sint$, $0<t<\frac{\pi }{2}$. Ta có: $dx=costdt$

và $\sqrt{1-x^2}=\sqrt{1-si{n}^{2}t}$$=\sqrt{co{s}^{2}t}=\left|cost\right|=cost.$

Đổi cận: $\{\begin{array}{l}x=0\Rightarrow t=0\\ x=1\Rightarrow t=\frac{\pi }{2}\end{array}$

$\begin{array}{l}\Rightarrow \underset{0}{\overset{1}{\int }}\sqrt{1-x^2}dx\\ =\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sqrt{1-{\sin }^{2}t}\cos tdt\\ =\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\cos }^{2}tdt=\frac{1}{2}\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(1+\cos 2t\right)dt\\ =\frac{1}{2}{\left(t+\frac{\sin 2t}{2}\right)|}_0^{\frac{\pi }{2}}\\ =\frac{1}{2}.\frac{\pi }{2}=\frac{\pi }{4}\end{array}$

c)

Đặt: $u=1+x.e^x$

$\Rightarrow du=0+\left(e^x+x.e^x\right)dx$$=e^x\left(1+x\right)dx$.

Đổi cận: $\{\begin{array}{l}x=0\Rightarrow u=1\\ x=1\Rightarrow u=1+e\end{array}$

$\begin{array}{l}\Rightarrow \underset{0}{\overset{1}{\int }}\frac{e^x\left(1+x\right)}{1+x{e}^x}dx=\underset{1}{\overset{1+e}{\int }}\frac{du}{u}={\ln \left|u\right||}_1^{1+e}\\ =\ln \left(1+e\right)-\ln 1=\ln \left(1+e\right)\end{array}$

d)

Đặt $x=a\sin t\Rightarrow dx=a\cos tdt$

Đổi cận: $\{\begin{array}{l}x=0\Rightarrow t=0\\ x=\frac{a}{2}\Rightarrow t=\frac{\pi }{6}\end{array}$

$\begin{array}{l}\Rightarrow \underset{0}{\overset{\frac{a}{2}}{\int }}\frac{1}{\sqrt{a^2-x^2}}dx=\underset{0}{\overset{\frac{\pi }{6}}{\int }}\frac{a\cos tdt}{\sqrt{a^2-a^2{\sin }^{2}t}}\\ =\underset{0}{\overset{\frac{\pi }{6}}{\int }}\frac{a\cos tdt}{a.\cos t}=\underset{0}{\overset{\frac{\pi }{6}}{\int }}dt={t|}_0^{\frac{\pi }{6}}=\frac{\pi }{6}\end{array}$.

Bài 4 trang 113 SGK Giải tích 12: Sử dụng phương pháp tích phân từng phần, hãy tính tích phân:

a) ${\int }_0^{\frac{\pi }{2}}(x+1)\sin xdx$

b) ${\int }_1^e{x}^2\ln xdx$

c) ${\int }_0^1\ln (1+x)dx$; 

d) ${\int }_0^1(x^2-2x-1)e^{-x}dx$

Phương pháp giải:

Phương pháp tích phân từng phần: $\underset{a}{\overset{b}{\int }}udv={uv|}_a^b-\underset{a}{\overset{b}{\int }}vdu$.

a) Đặt $\{\begin{array}{l}u=x+1\\ dv=\sin xdx\end{array}$

b) Đặt $\{\begin{array}{l}u=\ln x\\ dv=x^{2}dx\end{array}$

c) Đặt $\{\begin{array}{l}u=\ln \left(1+x\right)\\ dv=dx\end{array}$

d) Đặt $\{\begin{array}{l}u=x^2-2x-1\\ dv=e^{-x}dx\end{array}$

Lời giải:

a)

Đặt $\{\begin{array}{l}u=x+1\\ dv=\sin xdx\end{array}$ $\Rightarrow \{\begin{array}{l}du=dx\\ v=-\cos x\end{array}$

$\begin{array}{l}\Rightarrow \underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(x+1\right)\sin xdx\\ ={-\left(x+1\right)\cos x|}_0^{\frac{\pi }{2}}+\underset{0}{\overset{\frac{\pi }{2}}{\int }}\cos xdx\\ ={-\left(x+1\right)\cos x|}_0^{\frac{\pi }{2}}+{\sin x|}_0^{\frac{\pi }{2}}\end{array}$

$=-\left(\frac{\pi }{2}+1\right)\cos \frac{\pi }{2}+\left(0+1\right)\cos 0$$+\sin \frac{\pi }{2}-\sin 0$

$=0+1+1-0=2$

b) 

Đặt $\{\begin{array}{l}u=\ln x\\ dv=x^{2}dx\end{array}$ $\Rightarrow \{\begin{array}{l}du=\frac{dx}{x}\\ v=\frac{x^3}{3}\end{array}$

$\begin{array}{l}\Rightarrow \underset{1}{\overset{e}{\int }}{x}^2\ln xdx\\ ={\left(\ln x.\frac{x^3}{3}\right)|}_1^e-\frac{1}{3}\underset{1}{\overset{e}{\int }}{x}^{2}dx\\ ={\left(\ln x.\frac{x^3}{3}\right)|}_1^e-{\frac{x^3}{9}|}_1^e\end{array}$

$\begin{array}{l}=\ln e.\frac{e^3}{3}-\ln 1.\frac{1^3}{3}-\left(\frac{e^3}{9}-\frac{1^3}{9}\right)\\ =\frac{e^3}{3}-0-\frac{e^3}{9}+\frac{1}{9}\\ =\frac{2e^3}{9}+\frac{1}{9}\\ =\frac{1}{9}\left(2e^3+1\right)\end{array}$

c)

Đặt $\{\begin{array}{l}u=\ln \left(1+x\right)\\ dv=dx\end{array}\Rightarrow \{\begin{array}{l}du=\frac{dx}{1+x}\\ v=x\end{array}$

$\begin{array}{l}\Rightarrow \underset{0}{\overset{1}{\int }}\ln \left(x+1\right)dx\\ ={\left(x.\ln \left(1+x\right)\right)|}_0^1-\underset{0}{\overset{1}{\int }}\frac{x}{x+1}dx\\ ={\left(x.\ln \left(1+x\right)\right)|}_0^1-\underset{0}{\overset{1}{\int }}\frac{x+1-1}{x+1}dx\\ ={\left(x.\ln \left(1+x\right)\right)|}_0^1-\underset{0}{\overset{1}{\int }}\left(1-\frac{1}{x+1}\right)dx\\ ={\left(x.\ln \left(1+x\right)\right)|}_0^1-{\left(x-\ln \left|x+1\right|\right)|}_0^1\end{array}$

$\begin{array}{l}=1.\ln \left(1+1\right)-0.\ln \left(0+1\right)\\ -\left(1-\ln |1+1|-0+\ln |0+1|\right)\\ =\ln 2-1+\ln 2\\ =2\ln 2-1\end{array}$

d)

Đặt $\{\begin{array}{l}u=x^2-2x+1\\ dv=e^{-x}dx\end{array}$$\Rightarrow \{\begin{array}{l}du=\left(2x-2\right)dx\\ v=-e^{-x}\end{array}$

$\begin{array}{l}\Rightarrow \underset{0}{\overset{1}{\int }}\left(x^2-2x-1\right)e^{-x}dx\\ ={-e^{-x}\left(x^2-2x-1\right)|}_0^1\\ +2\underset{0}{\overset{1}{\int }}\left(x-1\right)e^{-x}dx\\ ={-e^{-x}\left(x^2-2x-1\right)|}_0^1+2I_1\\ =2e^{-1}-1+2I_1\end{array}$

Đặt $\{\begin{array}{l}u=x-1\\ dv=e^{-x}\end{array}$$\Rightarrow \{\begin{array}{l}du=dx\\ v=-e^{-x}\end{array}$.

$\begin{array}{l}\Rightarrow I_1={-e^{-x}\left(x-1\right)|}_0^1+\underset{0}{\overset{1}{\int }}{e}^{-x}dx\\ ={-e^{-x}\left(x-1\right)|}_0^1{-e^{-x}|}_0^1\\ =-1-\left(e^{-1}-1\right)=-e^{-1}\end{array}$.

Vậy $I=2e^{-1}-1-2e^{-1}=-1$.

Bài 5 trang 113 SGK Giải tích 12: Tính các tích phân sau:

a) ${\int }_0^1(1+3x{)}^{\frac{3}{2}}dx$;

b) ${\int }_0^{\frac{1}{2}}\frac{x^3-1}{x^2-1}dx$

c) ${\int }_1^2\frac{\ln (1+x)}{x^2}dx$

Phương pháp giải:

a) $\underset{}{\overset{}{\int }}{\left(ax+b\right)}^n=\frac{1}{a}\frac{{\left(ax+b\right)}^{n+1}}{n+1}+C$.

b) +) Sử dụng hằng đẳng thức để rút gọn phân thức trong dấu tích phân.

+) Chia tử số cho mẫu số.

c) Sử dụng phương pháp tích phân từng phần, đặt $\{\begin{array}{l}u=\ln \left(1+x\right)\\ dv=\frac{1}{x^2}dx\end{array}$

Lời giải:

a)

$\begin{array}{l}\underset{0}{\overset{1}{\int }}{\left(1+3x\right)}^{\frac{3}{2}}dx={\frac{1}{3}.\frac{{\left(1+3x\right)}^{\frac{3}{2}+1}}{\frac{3}{2}+1}|}_0^1\\ ={\frac{2}{15}.{\left(1+3x\right)}^{\frac{5}{2}}|}_0^1=\frac{2}{15}\left(4^{\frac{5}{2}}-1\right)=\frac{2}{15}.31=\frac{62}{15}\end{array}$

b)

$\begin{array}{l}\underset{0}{\overset{\frac{1}{2}}{\int }}\frac{x^3-1}{x^2-1}dx=\underset{0}{\overset{\frac{1}{2}}{\int }}\frac{\left(x-1\right)\left(x^2+x+1\right)}{\left(x-1\right)\left(x+1\right)}dx\\ =\underset{0}{\overset{\frac{1}{2}}{\int }}\frac{x^2+x+1}{x+1}dx=\underset{0}{\overset{\frac{1}{2}}{\int }}\frac{x\left(x+1\right)+1}{x+1}dx\\ =\underset{0}{\overset{\frac{1}{2}}{\int }}\left(x+\frac{1}{x+1}\right)dx={\left(\frac{x^2}{2}+\ln \left|x+1\right|\right)|}_0^{\frac{1}{2}}\\ =\frac{1}{8}+\ln \frac{3}{2}\end{array}$

c)

Đặt  $\{\begin{array}{l}u=\ln \left(1+x\right)\\ dv=\frac{1}{x^2}dx\end{array}\Rightarrow \{\begin{array}{l}du=\frac{1}{1+x}dx\\ v=-\frac{1}{x}\end{array}$

$\begin{array}{l}\Rightarrow \underset{1}{\overset{2}{\int }}\frac{\ln \left(1+x\right)}{x^2}dx={-\frac{1}{x}\ln \left(1+x\right)|}_1^2+\underset{1}{\overset{2}{\int }}\frac{dx}{x\left(1+x\right)}\\ =-\frac{1}{2}\ln 3+\ln 2+\underset{1}{\overset{2}{\int }}\left(\frac{1}{x}-\frac{1}{1+x}\right)dx\\ =-\frac{1}{2}\ln 3+\ln 2+{\ln \left|\frac{x}{1+x}\right||}_1^2\\ =-\frac{1}{2}\ln 3+\ln 2+\ln \frac{2}{3}-\ln \frac{1}{2}\\ =\ln \frac{1}{\sqrt{3}}+\ln 2+\ln \frac{2}{3}-\ln \frac{1}{2}\end{array}$

$\begin{array}{l}=-\frac{1}{2}\ln 3+\ln 2+\ln 2-\ln 3+\ln 2\\ =3\ln 2-\frac{3}{2}\ln 3\end{array}$

Bài 6 trang 113 SGK Giải tích 12: Tính tích phân ${\int }_0^{1}x(1-x{)}^{5}dx$ bằng hai phương pháp:

a) Đổi biến số: $u=1-x$;

b) Tính tích phân từng phần.

Phương pháp giải:

a) Đổi biến $x$ thành $u$ bằng cách: Đặt $u=1-x$.

b) Đặt $\{\begin{array}{l}u=x\\ dv={\left(1-x\right)}^{5}dx\end{array}$

Lời giải:

a)

Đặt $u=1-x$

$\Rightarrow x=1-u\Rightarrow dx=-du$.

Đổi cận: $\{\begin{array}{l}x=0\Rightarrow u=1\\ x=1\Rightarrow u=0\end{array}$

$\begin{array}{l}\Rightarrow \underset{0}{\overset{1}{\int }}x{\left(1-x\right)}^{5}dx=-\underset{1}{\overset{0}{\int }}\left(1-u\right)u^{5}du\\ =\underset{0}{\overset{1}{\int }}\left(u^5-u^6\right)du={\left(\frac{u^6}{6}-\frac{u^7}{7}\right)|}_0^1\\ =\frac{1}{6}-\frac{1}{7}=\frac{1}{42}\end{array}$

b)

Đặt $\{\begin{array}{l}u=x\\ dv={\left(1-x\right)}^{5}dx\end{array}$$\Rightarrow \{\begin{array}{l}du=dx\\ v=-\frac{{\left(1-x\right)}^6}{6}\end{array}$

$\begin{array}{l}\Rightarrow \underset{0}{\overset{1}{\int }}x{\left(1-x\right)}^{5}dx=-x{\frac{{\left(1-x\right)}^6}{6}|}_0^1+\frac{1}{6}\underset{0}{\overset{1}{\int }}{\left(1-x\right)}^{6}dx\\ =-\frac{1}{6}{\frac{{\left(1-x\right)}^7}{7}|}_0^1=\frac{1}{42}\end{array}$

Lí thuyết Bài 2: Tích phân

1. Khái niệm và tính chất

a. Định nghĩa

Cho hàm số $f(x)$ liên tục trên đoạn $[a;b]$. Giả sử $F(x)$ là một nguyên hàm của hàm số $f(x)$ trên đoạn $[a;b]$, hiệu số $F(b)-F(a)$ được gọi là tích phân từ $a$ đến $b$ (hay tích phân xác định trên đoạn $[a;b]$ của hàm số $f(x)$.

Kí hiệu là : ${\int }_a^{b}f(x)dx$

Vậy ta có :${\int }_a^{b}f(x)dx=F(b)-F(a)=F(x){|}_a^b$

Chú ý : Trong trường hợp a = b, ta định nghĩa: ${\int }_a^{a}f(x)dx=0$

Trường hợp a>b, ta định nghĩa: ${\int }_a^{b}f(x)dx=-{\int }_b^{a}f(x)dx$

Tích phân không phụ thuộc vào chữ dùng làm biến số trong dấu tích phân, tức là :

${\int }_a^{b}f(x)dx={\int }_a^{b}f(t)dt={\int }_a^{b}f(u)du=...$ (vì đều bằng $F(b)-F(a)$)

b. Tính chất của tích phân

${\int }_a^{b}kf(x)dx=k{\int }_a^{b}f(x)dx$  ( với $k$ là hằng số)

${\int }_a^b\left[f\left(x\right)\pm g\left(x\right)\right]d\mathrm{x}={\int }_a^{b}f\left(x\right)d\mathrm{x}\pm {\int }_a^{b}g\left(x\right)d\mathrm{x}$

${\int }_a^{b}f(x)dx={\int }_a^{c}f(x))dx+{\int }_c^{b}f(x)dx$ (với $a<b<c$)

2. Phương pháp tinh tích phân

a. Phương pháp đổi biến số

Định lí. Cho hàm số $f(x)$ liên tục trên $[a;b]$. Giả sử hàm số $x=\phi \left(t\right)$ có đạo hàm liên tục trên đoạn $[\alpha ;\beta ]$ sao cho $\phi \left(\alpha \right)=a,\phi \left(\beta \right)=b$ và $a\le \phi \left(t\right)\le b,\mathrm{\forall }t\in \left[\alpha ;\beta \right]$. Khi đó:

${\int }_a^{b}f(x)dx={\int }_{\alpha }^{\beta }f(\phi \left(t\right)){\phi }^{\prime }(t)dt$

Chú ý. Có thể dử dụng phép biến đổi số ở dạng sau:

Cho hàm số f(x) liên tục trên đoạn [a;b]. Giả sử hàm số u=u(x) có đạo hàm liên tục trên đoạn [a;b] sao cho α ≤ u(x) ≤ β, ∀ x∈ [a;b]. Nếu f(x) =g[u(x)].u’(x) ∀ x∈ [a;b], trong đó g(u) liên tục trên đoạn [α;β] thì: 

${\int }_a^{b}f(x)dx={\int }_{u(a)}^{u(b)}g(u)du$

b. Phương pháp tính tích phân từng phần

Định lí. Nếu u =u(x) và v=v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a;b], thì :

${\int }_a^{b}u(x)v^{\prime }(x)dx=[u(x)v(x)]{|}_a^b-{\int }_a^b{u}^{\prime }(x)v(x)dx$

hay ${\int }_a^{b}udv=uv{|}_a^b-{\int }_a^{b}vdu$

3. Bất đẳng thức (phần kiến thức bổ sung).

Nếu f(x) liên tục và không âm trên đoạn [a;b] thì : ${\int }_a^{b}f(x)dx\ge 0$

Từ đó ta có:

Nếu g(x), f(x) liên tục trên đoạn [a;b] và 0 ≤ g(x) ≤ f(x), ∀ x ∈ [a;b] thì

${\int }_a^{b}g(x)dx\le {\int }_a^{b}f(x)dx$

Dấu ” = ” xảy ra khi và chỉ khi g(x) ≡ f(x).

Suy ra: Nếu f(x) liên tục trên đoạn [a;b] và m ≤ f(x) ≤ M, ∀ x ∈ [a;b] thì

$m(b-a)\le {\int }_a^{b}f(x)dx\le M(b-a)$

Tích phân các hàm số cơ bản

1. Tính tích phân sử dụng bảng nguyên hàm cơ bản

Khi tính tích phân các hàm số cơ bản (đa thức, lượng giác, mũ,…) các em cần chú ý sử dụng bảng nguyên hàm các hàm số cơ bản kết hợp với công thức Leibnitz:

$\underset{a}{\overset{b}{\int }}f\left(x\right)dx=F\left(b\right)-F\left(a\right)$

ở đó, $f\left(x\right)$ là hàm liên tục trên $\left[a;b\right]$ và $F\left(x\right)$ là một nguyên hàm của $f\left(x\right)$.

Bảng nguyên hàm

2. Tính tích phân có chứa dấu giá trị tuyệt đối

Đối với các tích phân dạng $\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx$, phương pháp chung là ta cố gắng phá dấu giá trị tuyệt đối hàm $f\left(x\right)$ trên từng khoảng nhỏ nằm trong khoảng $\left(a;b\right)$ rồi tính lần lượt các tích phân đó.

Các dạng toán về tích phân

1. Một số dạng toán thường gặp áp dụng phương pháp đổi biến

Dạng 1: Tính tích phân bằng phương pháp đổi biến $t=u\left(x\right)$.

– Bước 1: Đặt $t=u\left(x\right)$, đổi cận $\{\begin{array}{l}x=a\Rightarrow t=u\left(a\right)=a^{\prime }\\ x=b\Rightarrow t=u\left(b\right)=b^{\prime }\end{array}$ .

– Bước 2: Tính vi phân $dt=u^{\prime }\left(x\right)dx$.

– Bước 3: Biến đổi $f\left(x\right)dx$ thành $g\left(t\right)dt$.

– Bước 4: Tính tích phân $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\underset{a^{\prime }}{\overset{b^{\prime }}{\int }}g\left(t\right)dt$.

Ví dụ: Tính tích phân $\underset{0}{\overset{\sqrt{3}}{\int }}2x\sqrt{x^2+1}dx$.

Giải:

Đặt $t=\sqrt{x^2+1}\Rightarrow t^2=x^2+1$ $\Rightarrow 2tdt=2xdx$.

Đổi cận $\{\begin{array}{l}x=0\Rightarrow t=1\\ x=\sqrt{3}\Rightarrow t=2\end{array}$

Do đó: $\underset{0}{\overset{\sqrt{3}}{\int }}2x\sqrt{x^2+1}dx=\underset{1}{\overset{2}{\int }}t.2tdt={\frac{2}{3}{t}^3|}_1^2=\frac{2}{3}\left(2^3-1^3\right)=\frac{14}{3}$.

Dạng 2: Tính tích phân bằng phương pháp đổi biến $x=u\left(t\right)$.

– Bước 1: Đặt $x=u\left(t\right)$, đổi cận $\{\begin{array}{l}x=a\Rightarrow t=a^{\prime }\\ x=b\Rightarrow t=b^{\prime }\end{array}$.

– Bước 2: Lấy vi phân 2 vế $dx=u^{\prime }\left(t\right)dt$.

– Bước 3: Biến đổi $f\left(x\right)dx=f\left(u\left(t\right)\right).u^{\prime }\left(t\right)dt=g\left(t\right)dt$.

– Bước 4: Tính nguyên hàm theo công thức $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\underset{a^{\prime }}{\overset{b^{\prime }}{\int }}g\left(t\right)dt$

Ví dụ: Cho $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sqrt{1-x^2}\mathrm{d}x$, nếu đặt $x=\sin t$ thì:

A. $I=2\underset{0}{\overset{1}{\int }}\left(1+\cos 2t\right)\mathrm{d}t$

B. $I=\underset{0}{\overset{1}{\int }}\frac{1-\cos 2t}{2}\mathrm{d}t$

C. $I=\underset{0}{\overset{1}{\int }}\frac{1+\cos 2t}{2}\mathrm{d}t$

D. $I=\underset{0}{\overset{1}{\int }}\frac{\cos 2t-1}{2}\mathrm{d}t$

Giải:

Đặt $x=\sin t\iff dx=\cos tdt$ và $1-x^2=1-{\sin }^{2}t={\cos }^{2}t$

Đổi cận $\{\begin{array}{l}x=0\Rightarrow t=0\\ x=\frac{\pi }{2}\Rightarrow t=1\end{array}$

Suy ra

$I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sqrt{1-x^2}\mathrm{d}x=\underset{0}{\overset{1}{\int }}\sqrt{{\cos }^{2}t}\cos t\mathrm{d}t$ $=\underset{0}{\overset{1}{\int }}{\cos }^{2}t\mathrm{d}t=\underset{0}{\overset{1}{\int }}\frac{1+\cos 2t}{2}\mathrm{d}t$

Chọn C.

Chú ý:

Các dấu hiệu thường dùng phương pháp trên là:

2. Một số bài toán thường áp dụng phương pháp tích phân từng phần

Dạng 1: Tích phân có chứa hàm số logarit.

Tính tích phân $\underset{m}{\overset{n}{\int }}f\left(x\right)\ln \left(ax+b\right)dx$  (trong đó $f\left(x\right)$ là hàm số đa thức)

Phương pháp:

– Bước 1: Đặt $\{\begin{array}{l}u=\ln \left(ax+b\right)\\ dv=f\left(x\right)dx\end{array}\Rightarrow \{\begin{array}{l}du=\frac{a}{ax+b}dx\\ v=\int f\left(x\right)dx\end{array}$

– Bước 2: Tính tích phân theo công thức $\underset{m}{\overset{n}{\int }}f\left(x\right)\ln \left(ax+b\right)dx={uv|}_m^n-\underset{m}{\overset{n}{\int }}vdu$

Ví dụ: Tính tích phân $I=\underset{1}{\overset{e}{\int }}x\ln x\mathrm{d}x.$

Giải: Đặt $\{\begin{array}{l}u=\ln x\\ dv=xdx\end{array}\Rightarrow \{\begin{array}{l}du=\frac{dx}{x}\\ v=\frac{x^2}{2}\end{array}$

Khi đó $I=\frac{x^2\ln x}{2}|\begin{array}{l}{}^e\\ {}_1\end{array}-\frac{1}{2}\underset{1}{\overset{e}{\int }}x=\frac{e^2}{2}-\frac{x^2}{4}|\begin{array}{l}{}^e\\ {}_1\end{array}=\frac{e^2+1}{4}$

Dạng 2: Tích phân có chứa hàm số mũ.

Tính tích phân $\underset{m}{\overset{n}{\int }}f\left(x\right)e^{ax+b}dx$. (trong đó $f\left(x\right)$ là hàm số đa thức)

Phương pháp:

– Bước 1: Đặt $\{\begin{array}{l}u=f\left(x\right)\\ dv=e^{ax+b}dx\end{array}\Rightarrow \{\begin{array}{l}du=f^{\prime }\left(x\right)dx\\ v=\frac{1}{a}{e}^{ax+b}\end{array}$

– Bước 2: Tính tích phân theo công thức $\underset{m}{\overset{n}{\int }}f\left(x\right)e^{ax+b}dx={uv|}_m^n-\underset{m}{\overset{n}{\int }}vdu$

Ví dụ: Tính $I=\underset{0}{\overset{1}{\int }}\left(2x+3\right)e^x\mathrm{d}x$

Giải: Đặt $\{\begin{array}{l}u=2x+3\\ dv=e^{x}dx\end{array}\Rightarrow \{\begin{array}{l}du=2dx\\ v=e^x\end{array}$

Khi đó$I={\left(2x+3\right)e^x|}_0^1-\underset{0}{\overset{1}{\int }}2e^{x}dx={\left(2x+3\right)e^x|}_0^1-{2e^x|}_0^1=3e-1.$

Dạng 3: Tích phân có chứa hàm số lượng giác và hàm đa thức.

Tính tích phân $\underset{m}{\overset{n}{\int }}f\left(x\right)\sin \left(ax+b\right)dx$ hoặc $\underset{m}{\overset{n}{\int }}f\left(x\right)\cos \left(ax+b\right)dx$. (trong đó $f\left(x\right)$ là hàm số đa thức)

Phương pháp:

– Bước 1: Đặt $\{\begin{array}{l}u=f\left(x\right)\\ dv=\sin \left(ax+b\right)dx\end{array}\Rightarrow \{\begin{array}{l}du=f^{\prime }\left(x\right)dx\\ v=-\frac{1}{a}\cos \left(ax+b\right)\end{array}$ hoặc $\{\begin{array}{l}u=f\left(x\right)\\ dv=\cos \left(ax+b\right)dx\end{array}\Rightarrow \{\begin{array}{l}du=f^{\prime }\left(x\right)dx\\ v=\frac{1}{a}\sin \left(ax+b\right)\end{array}$

– Bước 2: Tính tích phân theo công thức $\underset{m}{\overset{n}{\int }}f\left(x\right)\sin \left(ax+b\right)dx={uv|}_m^n-\underset{m}{\overset{n}{\int }}vdu$ hoặc $\underset{m}{\overset{n}{\int }}f\left(x\right)\cos \left(ax+b\right)dx={uv|}_m^n-\underset{m}{\overset{n}{\int }}vdu$

Ví dụ: Tính tích phân $I=\underset{0}{\overset{\frac{\pi }{4}}{\int }}x\sin 2x\mathrm{d}x$

Giải: Đặt $\{\begin{array}{l}u=x\\ dv=\sin 2xdx\end{array}\Rightarrow \{\begin{array}{l}du=dx\\ v=-\frac{\cos 2x}{2}\end{array}.$

Khi đó$I=-\frac{x\cos 2x}{2}|{}_{\genfrac{}{}{0ex}{}{0}{}}^{\frac{\pi }{4}}+\frac{1}{2}\underset{0}{\overset{\frac{\pi }{4}}{\int }}\cos 2xdx=-\frac{x\cos 2x}{2}|{}_{\genfrac{}{}{0ex}{}{0}{}}^{\frac{\pi }{4}}+\frac{\sin 2x}{4}|{}_{\genfrac{}{}{0ex}{}{0}{}}^{\frac{\pi }{4}}=\frac{1}{4}.$

Dạng 4: Tích phân có chứa hàm số lượng giác và hàm số mũ.

Tính tích phân $\underset{m}{\overset{n}{\int }}{e}^{ax+b}\sin \left(cx+d\right)dx$ hoặc $\underset{m}{\overset{n}{\int }}{e}^{ax+b}\cos \left(cx+d\right)dx$.

– Bước 1: Đặt $\{\begin{array}{l}u=e^{ax+b}\\ dv=\sin \left(cx+d\right)dx\end{array}$  hoặc $\{\begin{array}{l}u=e^{ax+b}\\ dv=\cos \left(cx+d\right)dx\end{array}$

– Bước 2: Tính tích phân theo công thức $\underset{m}{\overset{n}{\int }}udv={uv|}_m^n-\underset{m}{\overset{n}{\int }}vdu$

Ví dụ: Tính $K=\underset{0}{\overset{\pi }{\int }}{e}^x\cos 2x\mathrm{d}x$

Giải: Đặt $\{\begin{array}{l}u=\cos 2x\\ dv=e^{x}dx\end{array}\Rightarrow \{\begin{array}{l}du=-2\sin 2xdx\\ v=e^x\end{array}$

Suy ra $K=\left(e^x\cos 2x\right)|\begin{array}{c}{}^{\pi }\\ {}_0\end{array}+2\underset{0}{\overset{\pi }{\int }}{e}^x\sin 2xdx=e^{\pi }-1+2M$

Tính $M=\underset{0}{\overset{\pi }{\int }}{e}^x\sin 2xdx$

Ta đặt $\{\begin{array}{l}{u}_1=\sin 2x\\ d{v}_1=e^{x}dx\end{array}\Rightarrow \{\begin{array}{l}d{u}_1=2\cos 2x\\ v_1=e^x\end{array}$

Suy ra $M=\left(e^x\sin 2x\right)|\begin{array}{c}{}^{\pi }\\ {}_0\end{array}-2\underset{0}{\overset{\pi }{\int }}{e}^x\cos 2x=-2K$

Khi đó $K=e^{\pi }-1+2\left(-2K\right)\iff 5K=e^{\pi }-1\iff K=\frac{e^{\pi }-1}{5}$

– Đối với dạng toán này, ta cần thực hiện hai lần tích phân từng phần.
– Ở bước 1, ta cũng có thể đặt $\{\begin{array}{l}u=e^{ax+b}\\ dv=\sin \left(cx+d\right)dx\end{array}$  hoặc $\{\begin{array}{l}u=e^{ax+b}\\ dv=\cos \left(cx+d\right)dx\end{array}$