Giải bài tập Toán lớp 12 Bài 3: Phép chia số phức
Trả lời câu hỏi giữa bài
Trả lời câu hỏi 1 trang 136 SGK Giải tích 12: Cho . Hãy tính và . Nêu nhận xét.
Phương pháp giải:
Tính rồi thực hiện các phép tính cộng, nhân số phức.
Lời giải:
Ta có: .
Khi đó
.
Nhận xét:
Tổng của hai số phức liên hợp của nhau là một số thực.
Tích của hai số phức liên hợp của nhau là một số thực.
Trả lời câu hỏi 2 trang 138 SGK Giải tích 12: Thực hiện các phép chia sau:
Phương pháp giải:
Nhân cả tử và mẫu với số phức liên hợp của mẫu.
Lời giải:
Câu hỏi và bài tập (trang 138 Giải tích 12)
Bài 1 trang 138 SGK Giải tích 12: Thực hiện các phép chia sau:
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
Nhân cả tử và mẫu với số phức liên hợp của mẫu.
Chú ý:
Lời giải:
a)
b)
c)
d)
Bài 2 trang 138 SGK Giải tích 12: Tìm nghịch đảo của số phức , biết:
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
Cho số phức Khi đó nghịch đảo của số phức là:
c) Nhân cả tử và mẫu với và sử dụng định nghĩa
Lời giải:
a)
b)
c)
d)
Bài 3 trang 138 SGK Giải tích 12: Thực hiện các phép tính sau:
a) ;
b)
c) ;
d) .
Phương pháp giải:
Áp dụng công thức nhân và chia các số phức để làm bài toán.
Một số công thức cơ bản:
Lời giải:
a)
b)
c)
d)
Bài 4 trang 138 SGK Giải tích 12: Giải các phương trình sau:
a) ;
b) ;
c) .
Phương pháp giải:
+) Sử dụng quy tắc chuyển vế đổi dấu.
+) Sử dụng công thức chia hai số phức.
Lời giải:
a)
Ta có
.
Vậy .
b)
Ta có
Vậy
c)
Vậy
Lý thuyết Bài 3: Phép chia số phức
Kiến thức cơ bản
Cho hai số phức và .
Khi đó
(Nhân cả tử và mẫu với (số phức liên hợp của mẫu)).
Chú ý: Với ta có:
– Số phức nghịch đảo của là:
– Thương của chia cho là:
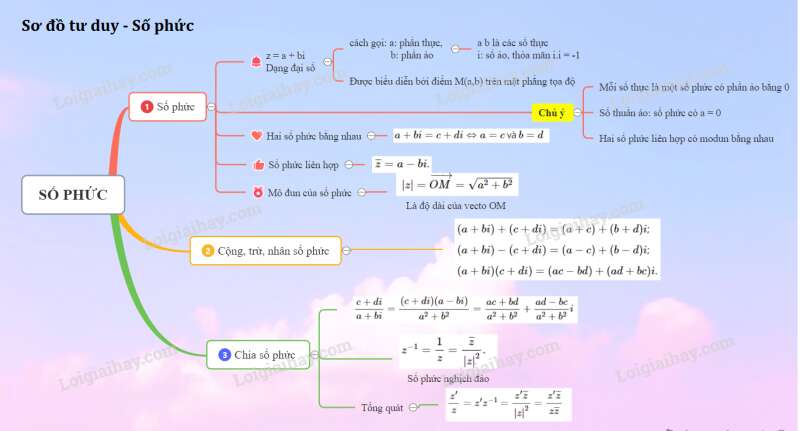
Sơ đồ tư duy về số phức