20 Bài tập Tập hợp các số hữu tỉ có đáp án – Toán 7

Bài tập Toán lớp 7 Bài 1: Tập hợp các số hữu tỉ

A. Bài tập Tập hợp các số hữu tỉ

1. Bài tập trắc nghiệm

Câu 1. Khẳng định nào trong các khẳng định sau là đúng?

A. Số 0 không phải là số hữu tỉ;

B. Số 0 là số hữu tỉ âm;

C. Số 0 là số hữu tỉ dương;

D. Số 0 là số hữu tỉ nhưng không phải là số hữu tỉ dương cũng không phải là số hữu tỉ âm.

Hướng dẫn giải

Đáp án đúng là: D

Số 0 là số hữu tỉ nhưng không phải là số hữu tỉ dương cũng không phải là số hữu tỉ âm.

Vậy ta chọn phương án D.

Câu 2. Điểm A trong hình dưới đây biểu diễn số hữu tỉ nào?

A. $\frac{2}{3}$ ;

B. $\frac{–2}{3}$ ;

C. $-\frac{1}{3}$ ;

D. – 1.

Hướng dẫn giải

Đáp án đúng là: B

Hình trên chia các đoạn thẳng đơn vị (chẳng hạn từ 0 đến 1) thành 3 đoạn bằng nhau, lấy một đoạn đó làm đơn vị mới thì đơn vị mới bằng $\frac{1}{3}$ đơn vị cũ.

Điểm A nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 2 đơn vị mới.

Do đó điểm A biểu diễn số $\frac{-2}{3}$ .

Mà $\frac{-2}{3}=\frac{2}{-3}.$

Suy ra điểm A biểu diễn số $\frac{2}{-3}.$

Vậy ta chọn phương án B.

Câu 3. Số hữu tỉ $\frac{x}{6}$ không thỏa mãn điều kiện $\frac{-1}{2}<\frac{x}{6}<\frac{1}{2}$ là:

A. $\frac{-1}{6}$ ;

B. $\frac{1}{6}$ ;

C. $\frac{1}{3}$ ;

D. $\frac{-2}{3}$ ;

Hướng dẫn giải

Đáp án đúng là: D

Ta có:$\frac{-1}{2}<\frac{x}{6}<\frac{1}{2}$ nên $\frac{-3}{6}<\frac{x}{6}<\frac{3}{6}$ .

Mà $\frac{x}{6}$ là số hữu tỉ nên x ∈ ℤ.

Suy ra $\frac{x}{6}\in \left\{\frac{-2}{6};\frac{-1}{6};0;\frac{1}{6};\right.\left.\frac{2}{6}\right\}$ .

Do đó:

• Phương án A số $\frac{-1}{6}$  thỏa mãn điều kiện nên A là sai.

• Phương án B số $\frac{1}{6}$  thỏa mãn điều kiện nên B là sai.

• Phương án C số $\frac{1}{3}=\frac{2}{6}$ thỏa mãn điều kiện nên C là sai.

• Phương án D số $\frac{-2}{3}=\frac{-4}{6}$ không thỏa mãn điều kiện nên D là đúng.

Vậy ta chọn phương án D.

2. Bài tập tự luận

Bài 1. Thay $?$  bằng kí hiệu ∈, ∉ thích hợp.       

a) 2023 $?$ ℚ;

b) $\frac{-2022}{2023}?$ ℤ;

c) $-\frac{4}{2}?$ ℕ;

d) 1,23 $?$ ℚ.

Hướng dẫn giải

a) 2023$?$ ℚ

Ta có: 2023 là số tự nhiên viết được dưới dạng $\frac{2023}{1}$ nên đây là số hữu tỉ.

Do đó 2023 $\in$  ℚ.

b) $\frac{-2022}{2023}?$ ℤ

Ta có: $\frac{-2022}{2023}$là số hữu tỉ, không phải là số nguyên.

Do đó $\frac{-2022}{2023}\notin$ ℤ.

c) $-\frac{4}{2}?$ ℕ

Ta có: $-\frac{4}{2}$ = –2  là số nguyên âm, không phải là số tự nhiên.

Do đó $-\frac{4}{2}\notin$  ℕ.

d) 1,23 $?$ ℚ.

Ta có: 1,23 = $\frac{123}{100}$ nên số 1,23 viết được dưới dạng phân số.

Do đó đây là số hữu tỉ.

Vậy 1,23 $\in$ ℚ.

Bài 2.

a) Trong các phân số sau, phân số nào biểu diễn số hữu tỉ $\frac{-2}{3}$ ?

$-\frac{-8}{12};\frac{4}{-6};\frac{-6}{9};-\frac{22}{33}.$

 

b) Tìm số đối của mỗi số sau: 1,3$\frac{-5}{8};-1\frac{1}{2};\frac{1}{-5}$.

Hướng dẫn giải

a) Ta có: $-\frac{-8}{12}=\frac{8}{12}=\frac{8:4}{12:4}=\frac{2}{3}\ne \frac{-2}{3};$

$\frac{4}{-6}=\frac{4:\left(-2\right)}{\left(-6\right):\left(-2\right)}=\frac{-2}{3};$

$\frac{-6}{9}=\frac{\left(-6\right):3}{9:3}=\frac{-2}{3};$

$-\frac{22}{33}=\frac{-22}{33}=\frac{\left(-22\right):11}{33:11}=\frac{-2}{3}.$

Vậy các phân số biểu diễn số hữu tỉ $\frac{-2}{3}$ là: $\frac{4}{-6};\frac{-6}{9};-\frac{22}{33}.$

b) Số đối của số 1,3 là ‒1,3;

Số đối của số $\frac{-5}{8}$ là $\frac{5}{8}$ .

Số đối của số $-1\frac{1}{2}$ là $1\frac{1}{2}$ .

Số đối của số  $\frac{1}{-5}$ là $\frac{1}{5}$ .

Bài 3.

a) Các điểm A, B, C, D trong hình dưới biểu diễn số hữu tỉ nào?

b) Biểu diễn các số hữu tỉ  $-1\frac{1}{2};1,5;\frac{5}{-2};-\frac{-7}{2}$trên trục số.

Hướng dẫn giải

a)

Dựa vào trục số ta thấy:

Mỗi đoạn thẳng đơn vị (chẳng hạn từ 0 đến 1) được chia thành 7 phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{7}$ đơn vị cũ).

– Xét các điểm nằm bên trái điểm 0:

• Điểm A cách điểm 0 một đoạn bằng 9 đơn vị mới nên điểm A biểu diễn số $\frac{-9}{7}$ .

• Điểm B cách điểm 0 một đoạn bằng 3 đơn vị mới nên điểm B biểu diễn số $\frac{-3}{7}$.

– Xét các điểm nằm bên phải điểm 0:

• Điểm C cách điểm 0 một đoạn bằng 2 đơn vị mới nên điểm C biểu diễn số $\frac{2}{7}$.

• Điểm D cách điểm 0 một đoạn bằng 6 đơn vị mới nên điểm D biểu diễn số $\frac{6}{7}$.

Vậy các điểm A, B, C, D lần lượt biểu diễn các số $\frac{-9}{7};\frac{-3}{7};\frac{2}{7};\frac{6}{7}$.

b) Biểu diễn các số hữu tỉ $-1\frac{1}{2};1,5;\frac{5}{-2};-\frac{-7}{2}$ trên trục số.

+) Biểu diễn số $-1\frac{1}{2}$:

• Ta có: $-1\frac{1}{2}=\frac{-3}{2}$

• Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 tới điểm 1) thành 2 phần bằng nhau, ta được đoạn đơn vị mới bằng $\frac{1}{2}$ đơn vị cũ.

Số hữu tỉ $\frac{–3}{2}$ được biểu diễn bởi điểm A nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 3 đơn vị mới (Hình vẽ).

+) Biểu diễn số 1,5:

• Ta có: 1,5 = $\frac{3}{2}.$

• Số hữu tỉ $\frac{3}{2}$được biểu diễn bởi điểm B nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 3 đơn vị mới (Hình vẽ).

+) Biểu diễn số $\frac{5}{-2}:$

• Ta có:$\frac{5}{-2}=\frac{-5}{2}.$

• Số hữu tỉ $\frac{-5}{2}$ được biểu diễn bởi điểm C nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 5 đơn vị mới (Hình vẽ).

+) Biểu diễn số $-\frac{-7}{2}:$

• Ta có: $-\frac{-7}{2}=\frac{7}{2}.$

• Số hữu tỉ $\frac{7}{2}$ được biểu diễn bởi điểm D nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 7 đơn vị mới (Hình vẽ).

Ta có các điểm A, B, C, D biểu diễn các số $-1\frac{1}{2};1,5;\frac{5}{-2};-\frac{-7}{2}$  trên trục số như hình vẽ sau:

Bài 4.

a) Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?

$\frac{-11}{9};1,125;-2\frac{1}{3};0;\frac{3}{7}.$

 

b) Hãy sắp xếp các số trên theo thứ tự tăng dần.

Hướng dẫn giải

a) Trong các số hữu tỉ $\frac{-11}{9};1,125;-2\frac{1}{3};0;\frac{3}{7}.$ thì có:

• Các số hữu tỉ dương là: 1,125;$\frac{3}{7}.$

• Các số hữu tỉ âm là:$\frac{-11}{9};-2\frac{1}{3}.$

• Số hữu tỉ không là số hữu tỉ dương cũng không là số hữu tỉ âm là: 0.

b)

• So sánh các số hữu tỉ dương: 1,125;$\frac{3}{7}.$

Ta có: 1,125 = $\frac{1125}{1000}=\frac{1125:125}{1000:125}=\frac{9}{8};$

Vì 3 < 7 và 7 > 0 nên $\frac{3}{7}<\frac{7}{7}$ hay $\frac{3}{7}<1$

Vì 9 > 8 và 8 > 0 nên $\frac{9}{8}>\frac{8}{8}$ hay $\frac{9}{8}>1$ .

Do đó $\frac{3}{7}<\frac{9}{8}$          (1)

• So sánh các số hữu tỉ âm: $\frac{-11}{9};-2\frac{1}{3}.$

Ta sẽ đi so sánh số đối của hai số trên là $\frac{11}{9}$ và $2\frac{1}{3}:$

Ta có: $\frac{11}{9}=1\frac{2}{9}.$

Ta thấy phần nguyên của số $1\frac{2}{9}$ bằng 1; phần nguyên của số $2\frac{1}{3}$bằng 2

Mà 1 < 2 nên $1\frac{2}{9}<2\frac{1}{3}.$

Do đó $-1\frac{2}{9}>-2\frac{1}{3}.$

Hay $\frac{-11}{9}>-2\frac{1}{3}.$  (2)

Mặt khác:

Số 0 luôn lớn hơn các số hữu tỉ âm và số 0 luôn nhỏ hơn các số hữu tỉ dương (3).

Từ (1), (2) và (3) ta có: $-2\frac{1}{3}<\frac{-11}{9}<0<\frac{3}{7}<\frac{9}{8}.$

Vậy sắp xếp các số theo thứ tự tăng dần là: $-2\frac{1}{3};\frac{-11}{9};0;\frac{3}{7};\frac{9}{8}.$

 Bài 5. Bảng dưới đây thể hiện nhiệt độ thấp nhất của một số ngày vào tháng 12/2021 tại Moskva (Nga):

Ngày	08/12/2021	09/12/2021	10/12/2021	11/12/2021	12/12/2021
Nhiệt độ thấp nhất (°C)	–8	–14	–16	–5	–3

(Nguồn: https://weather.com)

Trong những ngày trên, ngày nào là ngày tại Moskva ấm nhất? Lạnh nhất? Tại sao?

Hướng dẫn giải

Ta có: –16 < –14 < –8 < –5 < –3.

Vì nhiệt độ càng thấp thì càng lạnh, nhiệt độ càng cao thì càng ấm.

Do đó, tại Moskva, vào ngày 12/12/2021 sẽ ấm nhất và vào ngày 01/12/2021 sẽ lạnh nhất.

B. Lý thuyết Tập hợp các số hữu tỉ

1. Số hữu tỉ

– Số hữu tỉ là số được viết dưới dạng phân số $\frac{a}{b}$ với a, b ∈ ℤ, b ¹ 0.

– Các phân số bằng nhau biểu diễn cùng một số hữu tỉ.

– Tập hợp các số hữu tỉ được kí hiệu là ℚ.

Ví dụ:

• Các số $\frac{4}{5};\frac{-9}{10};\frac{3}{-8}$ là các số hữu tỉ.

• Các số 5; −3,4; 3$\frac{2}{5}$ là các số hữu tỉ vì:

5 = $\frac{5}{1}$ = $\frac{10}{2}$ = …;

−3,4 = $\frac{-34}{10}$ = $\frac{-17}{5}$ = …;

3$\frac{2}{5}$= $\frac{17}{5}$ = $\frac{34}{10}$ = …

– Chú ý: Mỗi số nguyên là một số hữu tỉ.

2. Thứ tự trong tập hợp các số hữu tỉ

– Với hai số hữu tỉ bất kì x, y ta luôn có: hoặc x = y hoặc x < y hoặc x > y.

– Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.

Số hữu tỉ bé hơn 0 gọi là số hữu tỉ âm.

Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.

Ví dụ: So sánh các cặp số hữu tỉ sau:

a) −0,8 và $\frac{-1}{5};$

b) −8$\frac{2}{3}$ và 0.

Hướng dẫn giải

a) −0,8 và $\frac{-1}{5}$

Ta có −0,8 = $\frac{-8}{10}$ và  $\frac{-1}{5}=\frac{-2}{10}$.

Vì −8 < −2 và 10 > 0 nên $\frac{-8}{10}<\frac{-2}{10}$.

Vậy – 0,8 < $\frac{-1}{5}$.

b) −8$\frac{2}{3}$ và 0

Ta có −8$\frac{2}{3}$= $\frac{-26}{3}$ và 0 = $\frac{0}{3}$.

Vì −26 < 0 và 3 > 0 nên  $\frac{-26}{3}<\frac{0}{3}$.

Vậy −8$\frac{2}{3}$ < 0.

Chú ý: Số hữu tỉ dương luôn luôn lớn hơn số hữu tỉ âm.

Ví dụ: Hãy sắp xếp các số hữu tỉ sau đây theo thứ tự tăng dần: $\frac{1}{5},\frac{-\text{ 2}}{5},\frac{3}{7},\frac{-\text{ 1}}{3},0.$

Hướng dẫn giải

• Ta so sánh $\frac{-2}{5};$ $\frac{-1}{3}$và 0.

Có:  $\frac{-\text{2}}{5}\text{\hspace{0.05em}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}}\frac{-\text{6}}{15};$ $\frac{-\text{1}}{3}\text{ = }\frac{-\text{5}}{15}$ và $0=\frac{0}{15}.$

Vì –6 < –5 < 0 nên $\frac{-\text{6}}{15}<\frac{-\text{5}}{15}\text{ <\hspace{0.17em}}\frac{0}{15}.$

Do đó $\frac{-\text{2}}{5}<\frac{-\text{1}}{3}<0.$         (1)

• Ta so sánh $\frac{1}{5}$ với $\frac{3}{7}.$

Có: $\frac{1}{5}\text{ = }\frac{7}{35}$ và $\frac{3}{7}\text{ = }\frac{15}{35}.$

Vì 7 < 15 nên $\frac{7}{35}\text{ < }\frac{15}{35}.$

Do đó $\frac{1}{5}<\frac{3}{7}.$         (2)

Lại có số hữu tỉ dương luôn lớn hơn số hữu tỉ âm.  (3)

Từ (1), (2) và (3) ta có: $\frac{-\text{2}}{5}<\frac{-\text{1}}{3}<0<\frac{1}{5}<\frac{3}{7}.$

Vậy sắp xếp các số theo thứ tự tăng dần là: $\frac{-\text{ 2}}{5}\text{; }\frac{-\text{ 1}}{3}\text{; 0; }\frac{1}{5}\text{; }\frac{3}{7}$ .

3. Biểu diễn số hữu tỉ trên trục số

– Trên trục số, mỗi số hữu tỉ được biểu diễn bởi một điểm. Điểm biểu diễn số hữu tỉ x được gọi là điểm x.

– Với hai số hữu tỉ bất kì x, y, nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.

Ví dụ:

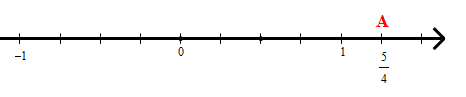
+ Để biểu diễn số hữu tỉ $\frac{5}{4}$ ta làm như sau:

• Chia đoạn thẳng đơn vị thành bốn phần bằng nhau, ta được đoạn thẳng mới bằng $\frac{1}{4}$ đơn vị cũ.

• Số hữu tỉ $\frac{5}{4}$ được biểu diễn bởi điểm A nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 5 đơn vị mới như trong hình dưới.

+ Để biểu diễn số hữu tỉ $\frac{4}{-3}$ trên trục số ta làm như sau:

• Viết $\frac{2}{-3}$ dưới dạng phân số với mẫu số dương $\frac{2}{-3}=\frac{-2}{3}.$

• Chia đoạn thẳng đơn vị thành ba phần bằng nhau, ta được đoạn đơn vị mới bằng $\frac{1}{3}$ đơn vị cũ.

• Số hữu tỉ $\frac{2}{-3}$ được biểu diễn bởi điểm B nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 2 đơn vị mới như hình dưới.

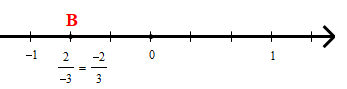
4. Số đối của một số hữu tỉ

– Hai số hữu tỉ có điểm biểu diễn trên trục số cách đều và nằm về hai phía điểm gốc O là hai số đối nhau, số này gọi là số đối của số kia.

– Số đối của số hữu tỉ x kí hiệu là −x.

Ví dụ:

$\frac{-5}{8}$ là số đối của $\frac{5}{8}$$;\frac{5}{8}$ là số đối của $\frac{-5}{8}$

0,123 là số đối của −0,123; −0,123 là số đối của 0,123.

Số đối của $1\frac{1}{2}$  (có $1\frac{1}{2}=\frac{3}{2}$) là $\frac{-3}{2}$ và ta viết là $-1\frac{1}{2}$ .

Chú ý:

– Mọi số hữu tỉ đều có một số đối.

– Số đối của số 0 là số 0.

– Với hai số hữu tỉ âm, số nào có số đối lớn hơn thì số đó nhỏ hơn.

Ví dụ: Tìm số đối của mỗi số sau: $\frac{12}{19};\frac{-1}{6};$  –2,22; 0; $2\frac{3}{4}.$

Hướng dẫn giải

Số đối của số $\frac{12}{19}$  là số $–\frac{12}{19}$

Số đối của số $\frac{-1}{6}$ là số $\frac{1}{6}$

Số đối của số –2,22 là số 2,22.

Số đối của số 0 là số 0.

Số đối của số $2\frac{3}{4}=\frac{11}{4}$là số $\frac{–11}{4}$ta viết là $-2\frac{3}{4}.$