Sách bài tập Toán 10 Bài 1 (Cánh diều): Hàm số và đồ thị

Giải SBT Toán lớp 10 Bài 1: Hàm số và đồ thị

Giải SBT Toán 10 trang 42 Tập 1

Bài 1 trang 42 SBT Toán 10 Tập 1: Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x?

A. x + 2y = 3.

B. y = $\sqrt{x^2-2x}$.

C. y = $\frac{1}{x}$.

D. x² + y² = 4.

Lời giải

Đáp án đúng là D

Xét công thức x + 2y = 3 ⇔ y = $\frac{–1}{2}$x + 3;

Với mỗi giá trị của x ta xác định được duy nhất một giá trị của y nên công thức này y là hàm số của x.

Xét công thức y = $\sqrt{x^2-2x}$

Với mỗi giá trị của x ta xác định được duy nhất một giá trị của y nên công thức này y là hàm số của x.

Xét công thức y = $\frac{1}{x}$

Với mỗi giá trị x ≠ 0 ta xác định được duy nhất một giá trị của y nên công thức này y là hàm số của x.

Xét công thức: x² + y² = 4 ⇔ y² =  – x² + 4 ⇔ y = $\pm \sqrt{-x^2+4}$.

Ta thấy ở công thức này, với mỗi giá trị của x thỏa mãn điều kiện – x² + 4 ≥ 0 ta xác định được 2 giá trị của y. Do đó công thức này không biểu diễn y là hàm số của x.

Bài 2 trang 42 SBT Toán 10 Tập 1: Cho đồ thị hàm số y = f(x) ở Hình 4. Phát biểu nào sau đây là đúng?

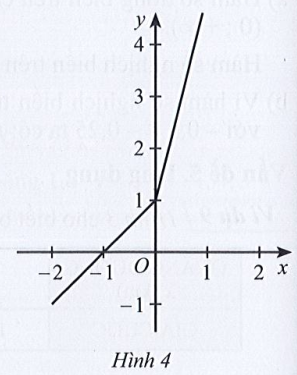
A. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 1.

B. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng – 1.

C. Hàm số đồng biến trên khoảng (– 1; +∞), nghịch biến trên khoảng ( – ∞; – 1).

D. Hàm số đồng biến trên ℝ.

Lời giải

Đáp án đúng là D

Quan sát đồ thị ta thấy:

Hàm số xác định trên ℝ, và trên ℝ hàm số đi lên nên hàm đồng biến trên ℝ. Do đó C sai và D đúng.

Đồ thị hàm số cắt Ox tại điểm có hoành độ bằng – 1. Do đó A sai.

Đồ thị hàm số cắt Oy tại điểm có tung độ bằng 1. Do đó B sai.

Bài 3 trang 42 SBT Toán 10 Tập 1: Tìm tập xác định của mỗi hàm số sau:

a) y = – x³ + 4x – 1;

b) y = $\sqrt{5-6x}$;

c) y = $\frac{4}{3x+1}$;

d) y = $\frac{1}{2x-1}-\sqrt{3-x}$;

e) y = $\frac{2x+3}{x^2+3x-4}$;

f) y = $\left\{\begin{array}{l}x-1khix>0\\ 5x+1khix<-1\end{array}\right.$.

Lời giải

a) Biểu thức – x³ + 4x – 1 xác định với mọi giá trị của x ∈ ℝ.

Do đó tập xác định của hàm số  y = – x³ + 4x – 1 là D = ℝ.

Vậy D = ℝ.

b) Biểu thức $\sqrt{5-6x}$ xác định khi 5 – 6x ≥ 0 ⇔ x ≤ $\frac{5}{6}$.

Do đó tập xác định của hàm số y = $\sqrt{5-6x}$ là D = $\left(-\infty ;\frac{5}{6}\right]$.

Vậy D = $\left(-\infty ;\frac{5}{6}\right]$.

c) Biểu thức $\frac{4}{3x+1}$ xác định khi 3x + 1 ≠ 0 ⇔ x ≠ $-\frac{1}{3}$.

Do đó tập xác định của hàm số y = $\frac{4}{3x+1}$ là D = ℝ \ $\left\{-\frac{1}{3}\right\}$.

Vậy D = ℝ \ $\left\{-\frac{1}{3}\right\}$.

d) Biểu thức $\frac{1}{2x-1}$ xác định khi 2x – 1 ≠ 0 ⇔ x ≠ $\frac{1}{2}$ và biểu thức $\sqrt{3-x}$ xác định khi 3 – x  ≥  0 ⇔ x ≤ 3.

Do đó tập xác định của hàm số y = $\frac{1}{2x-1}-\sqrt{3-x}$ là D = ( –∞; 3) \ $\left\{\frac{1}{2}\right\}$.

Vậy D =  ( –∞; 3) \ $\left\{\frac{1}{2}\right\}$.

e) Biểu thức $\frac{2x+3}{x^2+3x-4}$ xác định khi x² + 3x – 4 ≠ 0 ⇔ x ≠ 1 và x ≠ – 4.

Do đó tập xác định của hàm số y = $\frac{2x+3}{x^2+3x-4}$ là D = ℝ \{1; – 4}.

Vậy D = ℝ \{1; – 4}.

f) Biểu thức x – 1 luôn xác định với x > 0 và biểu thức 5x + 1 luôn xác định với x < – 1. Do đó tập xác định của hàm số y = $\left\{\begin{array}{l}x-1khix>0\\ 5x+1khix<-1\end{array}\right.$ là D = (– ∞; – 1) ∪ (0; + ∞).

Vậy D = (– ∞; – 1) ∪ (0; + ∞).

Bài 4 trang 42 SBT Toán 10 Tập 1: Cho hàm số: f(x) = $\left\{\begin{array}{l}-x+1khix<0\\ 0khix=0\\ 1khix>0\end{array}\right.$.

a) Tìm tập xác định của hàm số trên.

b) Tính giá trị của hàm số khi x = – 2; x = 0; x = 2 021.

Lời giải

a) Biểu thức – x + 1 luôn xác định với x < 0, biểu thức 0 luôn xác định với x = 0 và biểu thức 1 luôn xác định với x > 0.

Do đó tập xác định của hàm số f(x) là D = ℝ.

Vậy D = ℝ.

b) Với x = – 2 < 0 thì f(x) = – x + 1. Khi đó thay x = 2 vào hàm số ta được: f(– 2) = – (– 2) + 1 = 3.

Với x = 0 thì f(x) = 0. Khi đó thay x = 0 vào hàm số ta được: f(0) = 0.

Với x = 2 021 > 1 thì f(x) = 1. Khi đó thay x = 2 021 vào hàm số ta được: f(2 021) = 1.

Vậy giá trị của hàm số tại x = – 2; x = 0; x = 2 021 lần lượt là f(– 2) = 3; f(0) = 0 và f(2 021) = 1.

Giải SBT Toán 10 trang 43 Tập 1

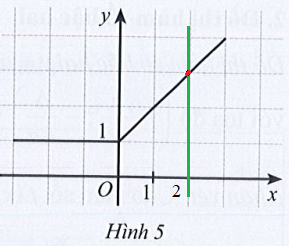
Bài 5 trang 43 SBT Toán 10 Tập 1: Quan sát đồ thị hàm số y = f(x) ở Hình 5.

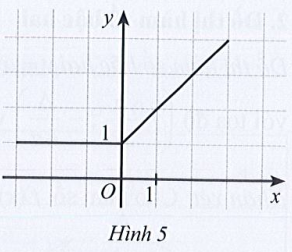
a) Trong các điểm có tọa độ (1 ; 2), (0 ; 0), (2 ; 3), điểm nào thuộc đồ thị hàm số, điểm nào không thuộc đồ thị hàm số?

b) Xác định f(0); f(3).

c) Tìm điểm thuộc đồ thị hàm số có tung độ bằng 1.

Lời giải 

a) +) Với điểm có tọa độ (1 ; 2) thì x = 1, y = 2.

Từ điểm x = 1 trên trục hoành ta dõng một đường thẳng đứng cắt đồ thị tại điểm có tung độ y = 2.

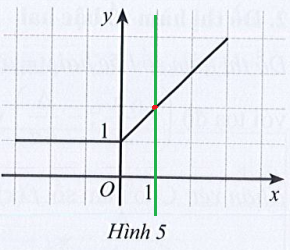
Do đó điểm có tọa độ (1 ; 2) thuộc vào đồ thị hàm số.

+) Với điểm có tọa độ (0 ; 0) thì x = 0, y = 0.

Từ điểm x = 0 trên trục hoành ta dõng một đường thẳng đứng cắt đồ thị tại điểm có tung độ y = 1 ≠ 0.

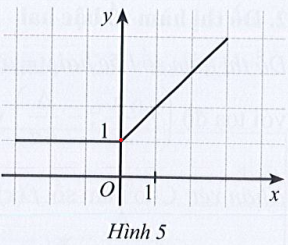
Do đó điểm có tọa độ (0 ; 0) không thuộc vào đồ thị hàm số.

+) Với điểm có tọa độ (2 ; 3) thì x = 2, y = 3.

Từ điểm x = 2 trên trục hoành ta dõng một đường thẳng đứng cắt đồ thị tại điểm có tung độ y = 3.

Do đó điểm có tọa độ (2 ; 3) thuộc vào đồ thị hàm số.

b) Giá trị f(0) là giá trị của hàm số tại điểm có hoành độ x = 0 hay chính là tung độ của điểm thuộc vào đồ thị có hoành độ bằng 0.

bằng 1. Do đó f(0) = 1.

Giá trị f(3) là giá trị của hàm số tại điểm có hoành độ x = 3 hay chính là tung độ của điểm thuộc vào đồ thị có hoành độ bằng 0.

Tại điểm x = 3 trên trục hoành dõng đường thẳng đứng cắt đồ thị tại điểm có tung độ bằng 4. Do đó f(3) = 4.

Vậy f(0) = 1 và f(3) = 4.

c) Gọi điểm thuộc đồ thị hàm số có tung độ bằng 1 là (a; 1).

Quan sát trên đồ thị hàm số ta thấy các điểm như trên thỏa mãn a ∈ [– 3; 0] thì tung độ đều bằng 1.

Vậy điểm điểm thuộc đồ thị hàm số có tọa độ (a; 1) với a ∈ [– 3; 0].

Bài 6 trang 43 SBT Toán 10 Tập 1: Cho bảng biến thiên hàm số y = f(x) như sau:

a) Tìm khoảng đồng biến, khoảng nghịch biến của hàm số y = f(x).

b) So sánh f(– 2021) và f(– 1); f($\sqrt{3}$) và f(2).

Lời giải

a) Dựa vào bảng biến thiên, ta thấy:

Hàm số đi lên trên khoảng (1; 3). Do đó hàm số đồng biến trên khoảng (1; 3).

Hàm số đi xuống trên khoảng (– ∞; 1) và (3; +∞). Do đó hàm số nghịch biến trên khoảng (– ∞; 1) và (3; +∞).

Vậy hàm số đồng biến trên khoảng (1; 3) và nghịch biến trên khoảng (– ∞; 1) và (3; +∞).

b) Ta có – 2021; – 1 ∈ (– ∞; 1) và – 2021 < – 1

Mà trên khoảng (– ∞; 1) hàm số nghịch biến nên f(– 2021) > f(– 1).

Ta có $\sqrt{3}$; 2 ∈ (1; 3) và $\sqrt{3}$ <  2

Mà trên khoảng (1; 3) hàm số đồng biến nên f($\sqrt{3}$) < f(2)

Vậy f(– 2021) > f(– 1) và f($\sqrt{3}$) < f(2).

Bài 7 trang 43 SBT Toán 10 Tập 1: Cho hàm số y = $\frac{-2}{x}$. Chứng tỏ hàm số đã cho đồng biến trên khoảng (–∞; 0) và (0; +∞).

Lời giải

Đặt y = f(x) = $\frac{-2}{x}$.

Tập xác định của hàm số D = ℝ \ {0}.

Lấy x₁, x₂ ∈ (–∞; 0) thỏa mãn x₁ < x₂ < 0

Vì x₁ < x₂ nên $\frac{2}{x_1}>\frac{2}{x_2}$ ⇒ $\frac{-2}{x_1}<\frac{-2}{x_2}$ hay f(x₁) < f(x₂).

Do đó hàm số đồng biến trên khoảng (–∞; 0).

Lấy x₁, x₂ ∈ (0; +∞) thỏa mãn 0 < x₁ < x₂

Vì x₁ < x₂ nên $\frac{2}{x_1}>\frac{2}{x_2}$ ⇒ $\frac{-2}{x_1}<\frac{-2}{x_2}$ hay f(x₁) < f(x₂).

Do đó hàm số đồng biến trên khoảng (0; +∞).

Vậy hàm số đồng biến trên khoảng (–∞; 0) và (0; +∞).

Bài 8 trang 43 SBT Toán 10 Tập 1: Một nhân viên bán hàng sẽ nhận được một mức lương cơ bản là 5 triệu đồng mỗi tháng và một khoản hoa hồng là 5% nếu tổng doanh số trên 10 triệu đồng trong tháng. Ngoài ra, nếu doanh số bán hàng hàng tháng là 20 triệu đồng hoặc nhiều hơn thì nhân viên bán hàng nhận được thêm tiền thưởng là 500 nghìn đồng.

a) Hãy biểu diễn thu nhập hàng tháng của nhân viên đó bằng một hàm số theo doanh số bán hàng.

b) Nếu doanh số trong 1 tháng của nhân viên đó là 30 triệu đồng thì nhân viên đó sẽ nhận được bao nhiêu tiền lương?

Lời giải

a) Gọi doanh số bán hàng hàng tháng của nhân viên đó là x (triệu đồng) (x > 0) và thu nhập hàng tháng của nhân viên đó là y (triệu đồng) (y > 0).

Ta có:

Nếu 0 < x ≤ 10 thì y = 5;

Nếu 10 < x < 20 thì y = 5 + 5%.x = 5 + 0,05x;

Nếu x ≥ 20 thì y = 5 + 5%.x + 0,5 = 5,5 + 0,05x.

Khi đó hàm số biểu diễn thu nhập hàng tháng của nhân viên đó theo doanh số bán hàng là $y=\left\{\begin{array}{l}5khi0<x\le 10\\ 5+0,05xkhi10<x<20\\ 5,5+0,05xkhix\ge 20\end{array}\right.$.

Vậy hàm số cần tìm là $y=\left\{\begin{array}{l}5khi0<x\le 10\\ 5+0,05xkhi10<x<20\\ 5,5+0,05xkhix\ge 20\end{array}\right.$.

b) Nếu x = 30 > 20 thì y = 5,5 + 0,05.30 = 7 triệu đồng.

Vậy nếu doanh số trong 1 tháng của nhân viên đó là 30 triệu đồng thì nhân viên đó sẽ nhận được số tiền lương là 7 triệu đồng.

Bài giảng Toán 10 Bài 1: Hàm số và đồ thị – Cánh diều

Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:

Bài ôn tập chương 2

Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

Bài 3: Dấu của tam thức bậc hai

Bài 4: Bất phương trình bậc nhất một ẩn

====== ****&**** =====