Sách bài tập Toán 10 Bài 5 (Cánh diều): Tích của một số với một vectơ

Giải SBT Toán lớp 10 Bài 5: Tích của một số với một vectơ

Giải SBT Toán 10 trang 99 Tập 1

Bài 47 trang 99 SBT Toán 10 Tập 1: Cho đoạn thẳng AB và O là trung điểm của đoạn thẳng AB. Khẳng định nào sau đây là đúng?

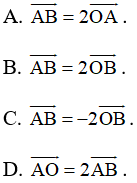
Lời giải:

Đáp án đúng là B

Vì O là trung điểm của AB nên OA = OB = $\frac{1}{2}$AB hay AB = 2OA = 2OB.

Ta có: $\overrightarrow{AB}$ và $\overrightarrow{OA}$ là hai vectơ ngược hướng nên $\overrightarrow{AB}=-2\overrightarrow{OA}$. Do đó A và D sai.

Ta lại có: $\overrightarrow{AB}$ và $\overrightarrow{OB}$ là hai vectơ cùng hướng nên $\overrightarrow{AB}=2\overrightarrow{OB}$. Do đó B đúng và C sai.

Bài 48 trang 99 SBT Toán 10 Tập 1: Cho tam giác ABC và M là trung điểm của BC, G là trọng tâm của tam giác. Khẳng định nào sau đây là đúng?

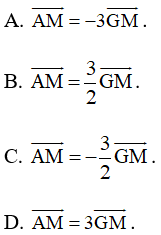
Lời giải:

Đáp án đúng là D

Vì G là trọng tâm tam giác ABC và AM là đường trung tuyến nên ta có:

AG = $\frac{2}{3}$AM hay AM = 3GM

Ta có hai vectơ $\overrightarrow{AM}$ và $\overrightarrow{GM}$ cùng hướng nên $\overrightarrow{AM}=3\overrightarrow{GM}$.

Vậy chọn D.

Bài 49 trang 99 SBT Toán 10 Tập 1: Cho $\overrightarrow{a}\ne \overrightarrow{0}$. Khẳng định nào sau đây là sai?

A. $\overrightarrow{a}$ và $4\overrightarrow{a}$ cùng phương.

B. $\overrightarrow{a}$ và $–4\overrightarrow{a}$ cùng phương.

C. $\overrightarrow{a}$ và $4\overrightarrow{a}$ không cùng hướng.

D. $\overrightarrow{a}$ và $–4\overrightarrow{a}$ ngược hướng.

Lời giải:

Đáp án đúng là C

Vì 4 > 0 nên $\overrightarrow{a}$ và $4\overrightarrow{a}$ cùng hướng nên $\overrightarrow{a}$ và $4\overrightarrow{a}$ cùng phương. Do đó A đúng, C sai.

Vì – 4 < 0 nên $\overrightarrow{a}$ và $–4\overrightarrow{a}$ ngược hướng nên $\overrightarrow{a}$ và $–4\overrightarrow{a}$ cùng phương. Do đó B, D đúng.

Bài 50 trang 99 SBT Toán 10 Tập 1: Cho đoạn thẳng AB và điểm C nằm giữa hai điểm A, B. Khẳng định nào sau đây là đúng?

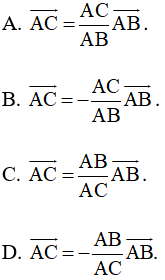
Lời giải:

Đáp án đúng là A

Vì điểm C nằm giữa hai điểm A, B nên hai vectơ $\overrightarrow{AC},\overrightarrow{AB}$ cùng hướng.

Do đó $\overrightarrow{AC}=\frac{AC}{AB}\overrightarrow{AB}$.

Vậy chọn A

Bài 51 trang 99 SBT Toán 10 Tập 1: Cho đoạn thẳng BC và điểm A nằm giữa hai điểm B, C. Khẳng định nào sau đây là đúng?

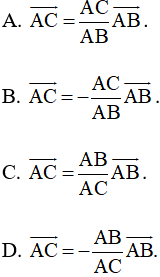
Lời giải:

Đáp án đúng là B

Vì điểm A nằm giữa hai điểm B và C nên hai vectơ $\overrightarrow{AC},\overrightarrow{AB}$ ngược hướng.

Do đó $\overrightarrow{AC}=-\frac{AC}{AB}\overrightarrow{AB}$.

Vậy chọn B

Giải SBT Toán 10 trang 100 Tập 1

Bài 52 trang 100 SBT Toán 10 Tập 1: Cho tam giác ABC. Xác định các điểm M, N, P trong mỗi trường hợp sau:

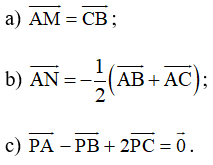
Ý b

Ý c

Lời giải:

a) Ta có: $\overrightarrow{AM}=\overrightarrow{CB}$

⇒ AM // CB, AM = CB và M, B cùng phía so với bờ AC

⇒ ACBM là hình bình hành

Vậy điểm M thỏa mãn ACBM là hình bình hành.

b) Gọi N’ là trung điểm của BC

Khi đó ta có: $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AN‘}$ hay $\overrightarrow{AN‘}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)$

⇒ $\overrightarrow{AN}=-\overrightarrow{AN‘}$

⇒ A là trung điểm của đoạn NN’

Vậy N là điểm đối xứng với N’ qua A.

c) Xét $\overrightarrow{PA}-\overrightarrow{PB}+2\overrightarrow{PC}=\overrightarrow{0}$

⇔ $\overrightarrow{BA}+2\overrightarrow{PC}=\overrightarrow{0}$

⇔ $2\overrightarrow{PC}=\overrightarrow{AB}$

⇒ Điểm P là điểm thỏa mãn PC // AB, P nằm cùng phía với A bờ BC sao cho 2PC = AB.

Vậy điểm P là điểm nằm trên đường thẳng song song với AB, nằm cùng phía với A so với BC sao cho 2PC = AB.

Bài 53 trang 100 SBT Toán 10 Tập 1: Cho tam giác ABC, kẻ tia phân giác AD. Đặt AB = b, AC = c. Chứng minh: $c\overrightarrow{DB}+b\overrightarrow{DC}=\overrightarrow{0}$.

Lời giải:

Xét tam giác ABC, có:

Ta có: D nằm giữa B và C nên $\overrightarrow{DB}$ và $\overrightarrow{DC}$ ngược hướng

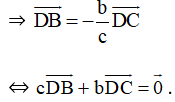
Bài 54* trang 100 SBT Toán 10 Tập 1: Cho hình bình hành ABCD. Lấy các điểm M, N, P thỏa mãn 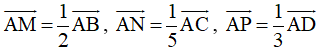. Đặt $\overrightarrow{AB}=\overrightarrow{a}$ và $\overrightarrow{AD}=\overrightarrow{b}$. Biểu thị các vec tơ   theo các vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$. Chứng minh ba điểm M, N, P thẳng hàng.

Lời giải:

Ta có: 

$\overrightarrow{AN}=\frac{1}{5}\overrightarrow{AC}=\frac{1}{5}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\frac{1}{5}\overrightarrow{AB}+\frac{1}{5}\overrightarrow{AD}=\frac{1}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$

$\overrightarrow{MN}=\overrightarrow{AN}-\overrightarrow{AM}=\frac{1}{5}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}=\frac{1}{5}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)-\frac{1}{2}\overrightarrow{AB}=-\frac{3}{10}\overrightarrow{AB}+\frac{1}{5}\overrightarrow{AD}=-\frac{3}{10}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$

$\overrightarrow{NP}=\overrightarrow{AP}-\overrightarrow{AN}=\frac{1}{3}\overrightarrow{AD}-\frac{1}{5}\overrightarrow{AC}=\frac{1}{3}\overrightarrow{AD}-\frac{1}{5}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=-\frac{1}{5}\overrightarrow{AB}+\frac{2}{15}\overrightarrow{AD}=-\frac{1}{5}\overrightarrow{a}+\frac{2}{15}\overrightarrow{b}$

Ta có $-\frac{3}{10}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}=\frac{3}{2}\left(-\frac{1}{5}\overrightarrow{a}+\frac{2}{15}\overrightarrow{b}\right)$ hay $\overrightarrow{MN}=\frac{3}{2}\overrightarrow{NP}$

Do đó M, N, P thẳng hàng.

Vậy $\overrightarrow{AN}=\frac{1}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$; $\overrightarrow{NP}=-\frac{1}{5}\overrightarrow{a}+\frac{2}{15}\overrightarrow{b}$; $\overrightarrow{MN}=-\frac{3}{10}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$ và ba điểm M, N, P thẳng hàng.

Bài 55* trang 100 SBT Toán 10 Tập 1: Cho tam giác ABC. Lấy các điểm D, E, M, N thỏa mãn $\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}$, $\overrightarrow{AE}=\frac{2}{5}\overrightarrow{AC}$, $\overrightarrow{BM}=\frac{1}{3}\overrightarrow{BC}$, $\overrightarrow{AN}=k\overrightarrow{AM}$ với k là số thực. Đặt $\overrightarrow{a}=\overrightarrow{AB}$, $\overrightarrow{b}=\overrightarrow{AC}$. Biểu thị các vectơ $\overrightarrow{AN}$, $\overrightarrow{DE}$, $\overrightarrow{EN}$ theo các vectơ $\overrightarrow{a}=\overrightarrow{AB}$, $\overrightarrow{b}=\overrightarrow{AC}$ và tìm k để ba điểm D, E, N thẳng hàng.

Lời giải:

Ta có: 

$\overrightarrow{AN}=k\overrightarrow{AM}=k.\left(\overrightarrow{AB}+\overrightarrow{BM}\right)=k.\left(\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC}\right)=k.\left[\overrightarrow{AB}+\frac{1}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\right]$

= $k.\left[\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\right]$ = $k.\left[\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}\right]$.

$\overrightarrow{DE}=\overrightarrow{AE}-\overrightarrow{AD}=\frac{2}{5}\overrightarrow{AC}-\frac{1}{3}\overrightarrow{AB}=-\frac{1}{3}\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}=-\frac{1}{3}\overrightarrow{a}+\frac{2}{5}\overrightarrow{b}$

$\overrightarrow{EN}=\overrightarrow{AN}-\overrightarrow{AE}=k.\left[\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\right]-\frac{2}{5}\overrightarrow{AC}=\frac{2k}{3}\overrightarrow{AB}+\left(\frac{k}{3}-\frac{2}{5}\right)\overrightarrow{AC}=\frac{2k}{3}\overrightarrow{a}+\left(\frac{k}{3}-\frac{2}{5}\right)\overrightarrow{b}$

Để ba điểm D, E, N thẳng hàng thì tồn tại t ∈ ℝ sao cho $\overrightarrow{EN}=t\overrightarrow{DN}$

⇔ $\frac{2k}{3}\overrightarrow{a}+\left(\frac{k}{3}-\frac{2}{5}\right)\overrightarrow{b}=t\left(-\frac{1}{3}\overrightarrow{a}+\frac{2}{5}\overrightarrow{b}\right)$ 

⇔ $\frac{2k}{3}\overrightarrow{a}+\left(\frac{k}{3}-\frac{2}{5}\right)\overrightarrow{b}=-\frac{t}{3}\overrightarrow{a}+\frac{2t}{5}\overrightarrow{b}$ 

⇔ $\left\{\begin{array}{l}\frac{2k}{3}=-\frac{t}{3}\\ \frac{k}{3}-\frac{2}{5}=\frac{2t}{5}\end{array}\right.$⇔ $\left\{\begin{array}{l}k=\frac{6}{17}\\ t=-\frac{12}{17}\end{array}\right.$

Do đó ba điểm D, E, N thẳng hàng khi k = $\frac{6}{17}$.

Vậy $\overrightarrow{AN}=k.\left[\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}\right]$, $\overrightarrow{DE}=-\frac{1}{3}\overrightarrow{a}+\frac{2}{5}\overrightarrow{b}$, $\overrightarrow{EN}=\frac{2k}{3}\overrightarrow{a}+\left(\frac{k}{3}-\frac{2}{5}\right)\overrightarrow{b}$ và với k = $\frac{6}{17}$ thì ba điểm D, E, N thẳng hàng.

Bài 56* trang 100 SBT Toán 10 Tập 1: Cho tam giác ABC, lấy các điểm A’, B’, C’ không trùng với đỉnh của tam giác và lần lượt thuộc các cạnh AB, BC, CA thỏa mãn $\frac{\text{AA}‘}{AB}=\frac{BB‘}{BC}=\frac{CC‘}{CA}$. Chứng minh hai tam giác ABC và A’B’C’ có cùng trọng tâm.

Lời giải:

Đặt $\frac{\text{AA}‘}{AB}=\frac{BB‘}{BC}=\frac{CC‘}{CA}=t$ (t > 0)

⇔ $\left\{\begin{array}{l}AA‘=tAB\\ BB‘=tBC\\ CC‘=tCA\end{array}\right.$

⇒ $\left\{\begin{array}{l}\overrightarrow{AA‘}=t\overrightarrow{AB}\\ \overrightarrow{BB‘}=t\overrightarrow{BC}\\ \overrightarrow{CC‘}=t\overrightarrow{CA}\end{array}\right.$ (vì các điểm A’, B’, C’ lần lượt thuộc các cạnh AB, BC, CA)

Gọi G là trọng tâm tam giác ABC nên $\overrightarrow{\text{GA}}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$

Ta có: 

Suy ra G cũng là trọng tâm của tam giác A’B’C’.

Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:

====== ****&**** =====