Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
264 bài tập trắc nghiệm chuyên đề chiều biến thiên của hàm số
Dạng 1: Xét tính đơn điệu của hàm số cho bởi biểu thức
Câu 1: Tìm khoảng nghịch biến của hàm số
\[y = \frac{1}{3}{x^3} – 2{x^2} + 3x – 2\].
Câu 2: Tìm các khoảng đồng biến, nghịch biến của hàm số
\[y = {x^3} – 3{x^2} + 1\].
Câu 3: Tìm các khoảng đồng biến, nghịch biến của hàm số
\[y = \frac{1}{3}{x^3} + 4x + 1\].
Câu 4: Tìm các khoảng đồng biến, nghịch biến của hàm số
\[y = – \frac{1}{3}{x^3} + 5{x^2} – 26x – 1\].
Câu 5: Tìm các khoảng đồng biến, nghịch biến của hàm số
\[y = \frac{1}{3}{x^3} + 3{x^2} + 9x – 1\].
Câu 6: Tìm các khoảng đơn điệu của hàm số \[y = {x^4} – 2{x^2}\].
Câu 7: Cho hàm số \[y = – \frac{1}{4}{x^4} + 2{x^2} – 1\]. Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số nghịch biến trên các khoảng (-2;0) và (2;+¥)
B. Hàm số nghịch biến trên các khoảng (-¥;-2) và (0;2)
C. Hàm số đồng biến trên các khoảng (-¥;-2) và (2;+¥)
D. Hàm số đồng biến trên các khoảng (-2;0) và (2;+¥)
Câu 8: Tìm các khoảng đơn điệu của hàm số \[y = {x^4} + 4{x^2}\].
Câu 9: Tìm các khoảng đơn điệu của hàm số \[y = – 2{x^4} + 4{x^2} – 7\].
Câu 10: Cho hàm số \[y = \frac{{2x + 1}}{{x + 1}}\]. Mệnh đề đúng là:
A. Hàm số đồng biến trên (-¥;-1) và (-1;+¥).
B. Hàm số nghịch biến trên (-¥;-1) và (-1;+¥)
C. Hàm số đồng biến trên (-¥;-1) và (1;+¥); nghịch biến trên (-1;1).
D. Hàm số đồng biến trên R.
Câu 11: Tìm các khoảng đơn điệu của hàm số \[y = \frac{{3x + 1}}{{1 – x}}\].
Câu 12: Tìm các khoảng nghịch biến của hàm số \[y = \frac{{3 – 2x}}{{x + 7}}\].
Câu 13: Hàm số \[y = x + \frac{1}{x}\] đồng biến trên khoảng nào dưới đây?
A. (0;+¥)
B. (-2;2)
C. (-2;0)
D. (2;+¥)
Câu 14: Cho hàm số \[y = \frac{{ – {x^2} + 2x – 1}}{{x + 2}}\]. Mệnh đề đúng là:
A. Hàm số đồng biến trên (-¥;5) và (1;+¥).
B. Hàm số nghịch biến trên (-¥;5) và (1;+¥).
C. Hàm số đồng biến trên (-¥;-2) và (-2;+¥))
D. Hàm số đồng biến trên R.
Câu 15: Tìm các khoảng nghịch biến của hàm số:
\[y = \frac{{ – {x^2} + 2x – 1}}{{x + 2}}\].
Câu 16: Tìm các khoảng đồng biến và nghịch biến của hàm số
\[y = \frac{{{x^2} + 4x + 4}}{{x + 1}}\].
Câu 17: Tìm các khoảng đồng biến và nghịch biến của hàm số:
\[y = \frac{{ – {x^2} – x + 5}}{{x + 2}}\].
Câu 18: Tìm các khoảng đồng biến, nghịch biến của hàm số
\[y = \frac{{ – 2x + 1}}{{{x^2} – 3x + 2}}\].
Câu 19: Tìm các khoảng đơn điệu của hàm số
\[y = \frac{{x + 1}}{{{x^2} – 4x + 4}}\].
Câu 20: Tìm các khoảng đơn điệu của hàm số
\[y = \frac{{x – 1}}{{{x^2} + x + 2}}\].
Câu 21: Tìm các khoảng đơn điệu của hàm số
\[y = {\left( {\frac{{x – 1}}{{x + 1}}} \right)^2}\].
Câu 22: Tìm các khoảng đơn điệu của hàm số
\[y = \frac{{\tan x – 2}}{{\tan x – 1}}\] trên \[\left( {0;\frac{\pi }{4}} \right)\].
Câu 23: Tìm các khoảng đơn điệu của hàm số
y = sin2x – 2cosx – 2x với \[x \in \left( { – \frac{\pi }{2};\frac{\pi }{2}} \right)\]
Câu 24: Cho hàm số \[y = f(x) = {x^3} + {x^2} + 8x + \cos x\], với hai số thực a, b sao cho a < b. Hãy so sánh \[f(a)\] với \[f(b)\]?
Câu 25: Tìm các khoảng đồng biến, nghịch biến của hàm số \[y = \left\{ {\begin{array}{*{20}{c}}{ – x + 2neux < – 1}\\{ – 2{x^2} + 2x + 7neu – 1 \le x \le 2}\\{3x – 3neux > 2}\end{array}} \right.\]
Câu 26: Tìm các khoảng đồng biến, nghịch biến của hàm số:
a) \[y = \left| {{x^2} – 2x – 3} \right|\].
b) \[y = \left| {{x^2} – 4x + 3} \right| + 4x + 3\].
Câu 27: Tìm các khoảng đồng biến và nghịch biến của hàm số: \[y = \sqrt {x + 1} + \sqrt {8 – x} + \sqrt {(1 + x)(8 – x)} \]
Câu 28: Hàm số \[y = \frac{{2x – 3}}{{\sqrt {{x^2} – 1} }}\] nghịch biến trên khoảng nào trong các khoảng dưới đây?
A. (-¥;- 1) và \[\left( {1;\frac{3}{2}} \right)\].
B. \[\left( {\frac{3}{2}; + \infty } \right)\].
C. \[\left( {1;\frac{3}{2}} \right)\].
D. (-¥;-1).
Câu 29: Hàm số \[y = \sqrt {{x^2} – 2x} \] đồng biến trên khoảng nào trong các khoảng dưới đây?
A. (1;+¥).
B. (2;+¥) .
C. (1;2).
D. (-¥;0).
Câu 30: Tìm các khoảng đơn điệu của hàm số \[y = x\sqrt {4 – {x^2}} \].
Câu 31: Tìm các khoảng đơn điệu của hàm số \[y = \frac{{x – 1}}{{\sqrt {{x^2} + 1} }}\].
Câu 32: Tìm các khoảng đơn điệu của hàm số
\[y = \sqrt {x + 1} ({x^2} – x – 20)\].
Câu 33: Tìm các khoảng đồng biến, nghịch biến của hàm số
\[y = \sqrt {x + 2} ({x^2} + 2x + 3)\].
Câu 34: Tìm các khoảng đơn điệu của hàm số \[y = \frac{{\sqrt {{x^2} + 4} }}{{x + 2}}\].
Câu 35: Xét sự biến thiên của hàm số \[y = \frac{x}{2} + {\sin ^2}x\] trên khoảng (0;p ) .
Câu 36: Hàm số y = 2sinx + cos2x, x Î [0;p] đồng biến trên khoảng nào trong các khoảng dưới đây?
A. \[\left( {0;\frac{\pi }{6}} \right)\].
B. \[\left( {\frac{\pi }{6};\frac{\pi }{2}} \right)\].
C. \[\left( {\frac{{5\pi }}{6};\pi } \right)\].
D. \[\left( {\frac{\pi }{6};\frac{{5\pi }}{6}} \right)\].
Câu 37: Tìm các khoảng đồng biến, nghịch biến của hàm số
\[y = \frac{{\sqrt { – {x^2} + 2x + 3} }}{{x + 2}}\].
Câu 38: Hàm số \[y = \frac{{mx – 1 – {m^2}}}{{x + 1}}\], (m là tham số). Mệnh đề nào dưới đây là đúng?
A. Hàm số đồng biến trên các khoảng xác định.
B. Hàm số đồng biến trên khoảng (-¥;+)
C. Hàm số đồng biến trên R \ {-1} .
D. Hàm số nghịch biến trên các khoảng xác định.
Câu 39: Cho hàm số \[y = f(x)\] có đạo hàm \[f'(x) = {x^2} + 1,\forall x \in R\]. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng (-¥;0).
B. Hàm số nghịch biến trên khoảng (1;+¥).
C. Hàm số nghịch biến trên khoảng (-1;1) .
D. Hàm số đồng biến trên khoảng (-¥;+¥).
Câu 40: Cho hàm số \[y = f(x)\] có đồ thị như hình vẽ. Mệnh đề nào dưới đây là đúng?
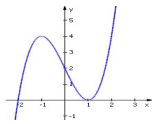
A. Hàm số nghịch biến trên khoảng (-¥;1).
B. Hàm số nghịch biến trên khoảng (1;+¥).
C. Hàm số nghịch biến trên khoảng (-1;1) .
Câu 41: Cho hàm số \[y = f(x)\] có đạo hàm \[f'(x) = \left( {{x^2} – 1} \right){\left( {x – 2} \right)^2}\left( {x – 3} \right)\]. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng (-¥;1).
B. Hàm số nghịch biến trên khoảng (-1;1) .
C. Hàm số nghịch biến trên khoảng (1;3).
D. Hàm số đồng biến trên khoảng (1;3).
Câu 42: Cho hàm số \[y = {x^4} – 2{x^2}\]. Mệnh đề nào dưới đây là đúng?
A. Hàm số đồng biến trên khoảng (-¥;-2)
B. Hàm số nghịch biến trên khoảng (-¥;-2)
C. Hàm số đồng biến trên khoảng (-1;1)
D. Hàm số nghịch biến trên khoảng (-1;1)
Dạng 2: Tìm khoảng đơn điệu của hàm số thông qua bảng biến thiên
Câu 43: Cho hàm số \[f(x)\] có bảng biến thiên như sau:
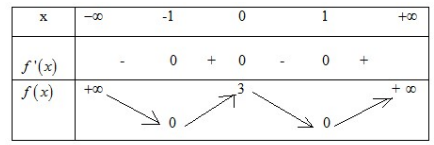
Hàm số đã cho đồng biến trên khoảng nào sau đây?
A. (-¥;-1)
B. (0;1)
C. (-1;0)
D. (-1;+¥)
Câu 44: Cho hàm số \[y = f(x)\] có bảng xét dấu đạo hàm như sau
![]()
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng (-¥;-2)
B. Hàm số đồng biến trên khoảng (-2;0)
C. Hàm số đồng biến trên khoảng (-¥;0)
D. Hàm số nghịch biến trên khoảng (0; 2)
Câu 45: Cho hàm số \[y = f(x)\] có bảng biến thiên như sau
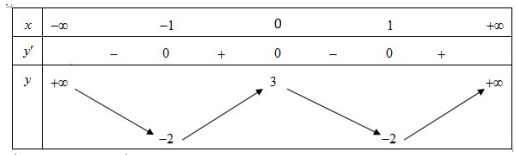
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (-1;0)
B. (-¥;0)
C. (1;+¥)
D. (0;1)
Câu 46: Cho hàm số \[f(x)\] có bảng biến thiên như sau:
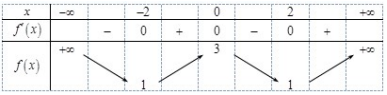
Hàm số đã cho đồng biến trên khoảng nào dưới đây
A. (0;+¥).
B. (0; 2).
C. (-2;0) .
D. (-¥;-2).
Câu 47: Cho hàm số \[y = f(x)\] có bảng biến thiên như sau :
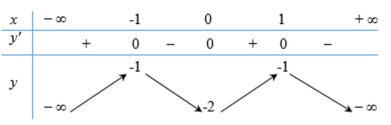
Câu 48: Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. (0;1)
B. (1;+¥)
C. (-¥;1)
D. (-1;0)
Câu 49: Cho hàm số có bảng biến thiên như sau
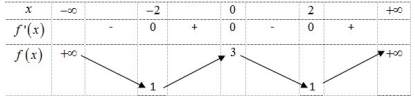
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (0;2).
B. (0;+¥)
C. (-2;0)
D. (2;+¥)
Câu 50: Cho hàm số \[y = f(x)\] có bảng biến thiên như sau:
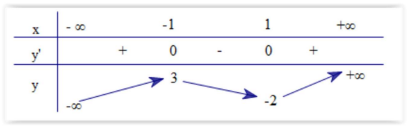
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. (-1;+¥).
B. (1;+¥).
C. (-1;1).
D. (-¥;1).
Câu 51: Cho hàm số \[y = f(x)\] có bảng biến thiên như sau
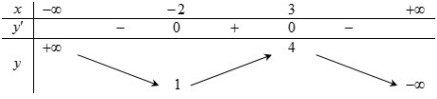
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. (-2;3)
B. (3;+¥)
C. (-¥;-2)
D. (-2;+¥)
Câu 52: Cho hàm số \[y = f(x)\] có bảng biến thiên như sau:
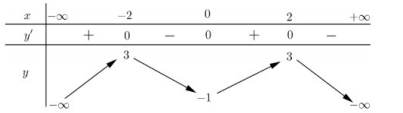
Hàm số \[y = f(x)\] nghịch biến trên khoảng nào dưới đây?
A. (0;+¥)
B. (-¥;-2)
C. (0;2)
D. (-2;0)
Xem thêm