Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu bao gồm các nội dung sau
Dạng 1. Các bài toán liên quan lý thuyết định nghĩa, tính chất, ứng dụng của phép tịnh tiến.
Dạng 2. Xác định ảnh của một điểm hoặc một hình qua phép tịnh tiến bằng phương pháp tọa độ
Các dạng toán phép dời hình và phép đồng dạng trong mặt phẳng
Phép tịnh tiến
Phần A. Câu hỏi
Dạng 1. Các bài toán liên quan lý thuyết định nghĩa, tính chất, ứng dụng của phép tịnh tiến
Câu 1. Có bao nhiêu phép tịnh tiến biến đường thẳng thành chính nó?
A. 0 .
B. 1 .
C. 2 .
D. Vô số.
Câu 2. Có bao nhiêu phép tịnh tiến biến đường tròn thành chính nó?
A. 0 .
B. 1 .
C. 2 .
D. Vô số.
Câu 3. Có bao nhiêu phép tịnh tiến biến hình vuông thành chính nó?
A. 0 .
B. 1 .
C. 2 .
D. Vô số.
Câu 4. Phép tịnh tiến không bảo toàn yếu tố nào sau đây?
A. Khoảng cách giữa hai điểm.
B. Thứ tự ba điểm thẳng hàng.
C. Tọa độ của điểm.
D. Diện tích.
Câu 5. (THPT YÊN LẠC – LẦN 4 – 2018) Cho hình chữ nhật M N P Q. Phép tịnh tiến theo véc tơ \(\overrightarrow {MN} \) biến điểm Q thành điểm nào?
A. Điểm Q.
B. Điểm N.
C. Điểm M.
D. Điểm P.
Câu 6. (THPT HẬU LỘC 2 – TH – 2018) Chọn khẳng định sai trong các khẳng định sau:
A. Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.
B. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
C. Phép tịnh tiến biến một đường tròn thành một đường tròn có cùng bán kính.
D. Phép tịnh tiến biến một đường thẳng thành một đường thẳng song song với nó.
Câu 7. (CTN – LẦN 1 – 2018) Có bao nhiêu phép tịnh tiến biến một đường tròn thành chính nó?
A. 0 .
B. 2 .
C. 3 .
D. 1 .
Câu 8. Kết luận nào sau đây là sai?
A. \({T_{\vec u}}(A) = B \Leftrightarrow \overrightarrow {AB} = \vec u\quad \)
B. \({T_{\overrightarrow {AB} }}(\;{\rm{A}}) = {\rm{B}}\)
C. \({T_{\vec 0}}(B) = B\)
C. \({T_{2\overrightarrow {AB} }}(M) = N \Leftrightarrow \overrightarrow {AB} = 2\overrightarrow {MN} \)
Câu 9. Giả sử \({T_{\bar v}}(M) = {M^\prime };{T_{\bar v}}(N) = {N^\prime }\). Mệnh đề nào sau đây saí?
A. \(\overrightarrow {{M^\prime }{N^\prime }} = \overrightarrow {MN} \).
B. \(\overrightarrow {M{M^\prime }} = \overrightarrow {N{N^\prime }} \)
C. \(M{M^\prime } = N{N^\prime }\).
D. \(MN{M^\prime }{N^\prime }\) là hình bình hành.
Câu 10. Cho hai đường thẳng \({d_1}\) và \({d_2}\) cắt nhau. Có bao nhiêu phép tịnh tiến biến \({d_1}\) thành \({d_2}\)
A. Không.
B. Một.
C. Hai.
D. Vô số.
Câu 11. (THPT LÝ THÁI TỔ – BẮC NINH – 2018) Trong mặt phẳng với hệ trục tọa độ Oxy cho \(A(2; – 3),B(1;0)\).Phép tịnh tiến theo \(\vec u(4; – 3)\) biến điểm A, B tương ứng thành \({A^\prime },{B^\prime }\) khi đó, độ dài đoạn thẳng \({A^\prime }{B^\prime }\) bằng:
A. \({A^\prime }{B^\prime } = \sqrt {10} \).
B. \({A^\prime }{B^\prime } = 10\).
C. \({A^\prime }{B^\prime } = \sqrt {13} \).
D. \({A^\prime }{B^\prime } = \sqrt 5 \).
Câu 12. Trong mặt phẳng tọa độ Oxy, cho hai điểm \(M(0;2),N( – 2;1)\) và véctơ \(\vec v = (1;2)\).. Phép tịnh tiến theo véctơ \(\vec v\) biến M, N thành hai điểm \({M^\prime },{N^\prime }\) tương ứng. Tính độ dài \({M^\prime }{N^\prime }\).
A. \({M^\prime }{N^\prime } = \sqrt 5 \).
B. \({M^\prime }{N^\prime } = \sqrt 7 \).
C. \({M^\prime }{N^\prime } = 1\).
D. \({M^\prime }{N^\prime } = 3\).
Câu 13. Với hai điểm A, B phân biệt và \({T_{\vec v}}(A) = {A^\prime },{T_{\vec v}}(B) = {B^\prime }\) với \(\vec v \ne \vec 0\). Mệnh đề nào sau đây đúng?
A. \(\overrightarrow {{A^\prime }{B^\prime }} = \vec v\).
B. \(\overrightarrow {{A^\prime }{B^\prime }} = \overrightarrow {AB} \).
C. \(\overrightarrow {AB} = \vec v\).
D. \(\overrightarrow {{A^\prime }{B^\prime }} + \overrightarrow {AB} = \vec 0\).
Câu 14. Cho hai đường thẳng \({d_1}\) và \({d_2}\) song song với nhau. Có bao nhiêu phép tịnh tiến theo vectơ \(\vec v \ne \vec 0\) biến \({d_1}\) thành \({d_2}\) ?
A. 0 .
B. 1 .
C. 2 .
D. Vô số.
Câu 15. Cho hình bình hành ABCD. Phép tịnh tiến \({T_{\overline {AB} + \overline {AD} }}\) biến điểm A thành điểm nào?
A. \({A^\prime }\) đối xứng với A qua C.
B. \({A^\prime }\) đối xứng với D qua C.
C. O là giao điểm của AC qua BD.
D. C.
Câu 16. Cho tam giác ABC có trọng tâm \(G,{T_{\overline {AG} }}(G) = M\). Mệnh đề nào là đúng?
A. M là trung điểm BC.
B. M trùng với A.
C. M là đỉnh thứ tư của hình bình hành BGCM.
D. M là đỉnh thứ tư của hình bình hành BCGM.
Câu 17. Cho lục giác đều ABCDEF tâm O. Tìm ảnh của qua phép tịnh tiến theo vectơ \(\overrightarrow {AB} \).
A. .
B. .
C. .
D. .
Câu 18. Cho hình bình hành ABCD tâm I. Kết luận nào sau đây sai?
A. \({T_{\overline {DC} }}(A) = B\).
B. \({T_{\overline {CD} }}(B) = A\).
C. \({T_{\overline {DI} }}(I) = B\).
D. \({T_{\overline {IA} }}(I) = C\)
Câu 19. Cho hình vuông ABCD tâm I. Gọi M, N lần lượt là trung điểm của AD, DC. Phép tịnh tiến theo vectơ nào sau đây biến thành ?
A. \(\overrightarrow {AM} \).
B. \(\overrightarrow {NI} \).
C. \(\overrightarrow {AC} \).
D. \(\overrightarrow {MN} \).
Câu 20. Cho hình bình hành ABCD. Có bao nhiêu phép tịnh tiến biến đường thẳng AB thành đường thẳng CD và biến đường thẳng AD thành đường thẳng BC ?
A. 0 .
B. 1 .
C. 2 .
D. Vô số.
Câu 21. Cho hình vuông ABCD tâm I. Gọi M, N lần lượt là trung điểm AD, DC. Phép tịnh tiến theo vectơ nào sau đây biến tam giác AMI thành INC
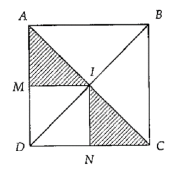
A. \(\overrightarrow {AM} \).
B. \(\overrightarrow {IN} \).
C. \(\overrightarrow {AC} \).
D. \(\overrightarrow {MN} \).
Câu 22. Cho hình bình hành ABCD tâm I. Kết luận nào sau đây là sai?
A. \({T_{\overline {AB} }}(D) = C\).
B. \({T_{\overline {CD} }}(B) = A\).
C. \({T_{\overline {AI} }}(I) = C\).
D. \({T_{\overline {ID} }}(I) = B\).
Câu 23. Trong các đối tượng: con cá (hình A ), con bướm (hình B, con mèo (hình C ), con ngựa (hình D ), hình nào có phép tịnh tiến?

Câu 24. Cho đường tròn (C ) có tâm O và đường kính A B. Gọi \(\Delta \) là tiếp tuyến của (C ) tại điểm A. Phép tịnh tiến theo vectơ \(\overrightarrow {AB} \) biến \(\Delta \) thành:
A. Đường kính của đường tròn (C ) song song với \(\Delta \).
B. Tiếp tuyến của (C ) tại điểm \(B\).
C. Tiếp tuyến của (C ) song song với A B.
D. Đường thẳng song song với \(\Delta \) và đi qua O
Câu 25. Cho hai điểm B, C cố định trên đường tròn (O;R) và A thay đổi trên đường tròn đó, BD là đường kính. Khi đó quỹ tích trực tâm H của là:
A. Đoạn thẳng nối từ A tới chân đường cao thuộc BC của .
B. Cung tròn của đường tròn đường kính BC.
C. Đường tròn tâm \({O^\prime }\) bán kính R là ảnh của (O;R) qua \({T_{\overline {HA} }}\).
D. Đường tròn tâm \({O^\prime }\), bán kính R là ảnh của (O;R) qua \({T_{\overline {DC} }}\).
Câu 26. Cho hình bình hành ABCD, hai điểm A, B cố định, tâm I di động trên đường tròn (C ). Khi đó quỹ tích trung điểm M của cạnh DC :
A. là đường tròn \(\left( {{C^\prime }} \right)\) là ảnh của \((C)\) qua \({T_{\overline {KI} }},K\) là trung điểm của BC.
B. là đường tròn \(\left( {{C^\prime }} \right)\) là ảnh của \((C)\) qua \({T_{\overline {KI} }},K\) là trung điểm của AB.
C. là đường thẳng BD.
D. là đường tròn tâm I bán kính ID.
Câu 27. Cho đường tròn (O ) và hai điểm A, B. Một điểm M thay đổi trên đường tròn (O). Tìm quỹ tích điểm \({M^\prime }\) sao cho \(\overrightarrow {M{M^\prime }} + \overrightarrow {MA} = \overrightarrow {MB} \).
A. \(\left( {{O^\prime }} \right) = {T_{\overrightarrow {AB} }}((O))\).
B. \(\left( {{O^\prime }} \right) = {T_{\overline {AM} }}((O))\).
C. \(\left( {{O^\prime }} \right) = {T_{\overrightarrow {BA} }}((O))\).
D. \(\left( {{O^\prime }} \right) = {T_{\overline {BM} }}((O))\).
Câu 28. Cho tứ giác lồi A B C D có và . Tính độ dài AD.
A. \(a\sqrt {2 + \sqrt 5 } \).
B. \(a\sqrt 3 \).
C. \(a\sqrt {2 + \sqrt 3 } \).
D. \(a\sqrt 5 \).
Câu 29. Cho tứ giác ABCD có . Tính độ dài BC.
A. 4 .
B. 5 .
C. 6 .
D. 2 .
Câu 30. Trên đoạn AD cố định dựng hình bình hành ABCD sao cho \(\frac{{AC}}{{AD}} = \frac{{BD}}{{AB}}\). Tìm quỹ tích đỉnh C.
A. Đường tròn tâm A, bán kính là \(AB\sqrt 3 \).
B. Đường tròn tâm A, bán kính là AC.
C. Đường tròn tâm A, bán kính là AD.
D. Đường tròn tâm A, bán kính là \(AD\sqrt 2 \).
Câu 31. Cho hai đường tròn có bán kính R cắt nhau tại M, N. Đường trung trực của M N cắt các đường tròn tại A và B sao cho A, B nằm cùng một phía với M N. Tính \(P = M{N^2} + A{B^2}\).
A. \(P = 2{R^2}\).
B. \(P = 3{R^2}\).
C. \(P = 4{R^2}\).
D. \(P = 6{R^2}\).
Câu 32. Cho hai đường tròn có bán kính R tiếp xúc ngoài với nhau tại K. Trên đường tròn này lấy điểm A, trên đường tròn kia lấy điểm B sao cho . Độ dài A B bằng bao nhiêu?
A. R.
B. \(R\sqrt 2 \).
C. \(R\sqrt 3 \).
D. 2 R.
Câu 33. Từ đỉnh B của hình bình hành ABCD kẻ các đường cao BK và BH của nó biết \(KH = 3,BD = 5\) . Khoảng cách từ B đến trực tâm \({H_1}\) của tam giác BKH có giá trị bằng bao nhiêu?
A. 4 .
B. 5 .
C. 6 .
D. 4,5 .
Dạng 2. Xác định ảnh của một điểm hoặc một hình qua phép tịnh tiến bằng phuơng pháp tọa dộ
Dạng 2.1 Điểm
Câu 34. (SGD và ĐT BẮC NINH 2018) Trong mặt phẳng vói hẹ tọa độ Ox y, cho điểm M(2;5). Phép tịnh tiến theo vectơ \(\vec v = (1;2)\) biến điểm M thành điểm \({M^\prime }\). Tọa độ điểm \({M^\prime }\) là:
A. \({M^\prime }(3;7)\).
B. \({M^\prime }(1;3)\).
C. \({M^\prime }(3;1)\).
D. \({M^\prime }(4;7)\).
Câu 35. (THPT CHUYÊN LƯOONG VĂN CHÁNH – PHÚ YÊN – 2018) Phép tịnh tiến biến gốc tọa độ O thành điểm A(1;2) sẽ biến điểm A thành điểm \({A^\prime }\) có tọa độ là:
A. \({A^\prime }(2;4)\).
B. \({A^\prime }( – 1; – 2)\).
C. \({A^\prime }(4;2)\).
D. \({A^\prime }(3;3)\).
Câu 36. (THPT XUÂN HÒA – VP – LẦN 1 – 2018) Cho \(\vec v = ( – 1;5)\) và điểm \({M^\prime }(4;2)\). Biết \({M^\prime }\) là ảnh của M qua phép tịnh tiến \({T_{\vec v}}\). Tìm M.
A. M(-4;10).
B. M(-3;5).
C. M(3;7).
D. M(5;-3).
Câu 37. (THPT CHU VĂN AN – HKI – 2018) Trong mặt phẳng tọa độ Oxy, tìm tọa độ điểm \({A^\prime }\) là ảnh của điểm A(-1;3) qua phép tịnh tiến theo vectơ \(\vec v = (2;1)\).
A. \({A^\prime }( – 1; – 4)\).
B. \({A^\prime }(1;4)\).
C. \({A^\prime }(1; – 4)\).
D. \({A^\prime }( – 1;4)\).
Xem thêm