Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
20 bài tập về khoảng cách từ điểm đến mặt phẳng (dạng 2) có lời giải chi tiết
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a , AD = 2a. Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy. Tính khoảng cách từ điểm A tới mặt phẳng (SBD)
A. \[\frac{a}{{\sqrt 5 }}\]
B. \[\frac{{2a}}{{\sqrt 5 }}\]
C. \[\frac{{3a}}{{\sqrt 5 }}\]
D. \[\frac{{4a}}{{\sqrt 5 }}\]
Câu 2. Cho hình chóp S.ABC có đáy là tam giác đều, hình chiếu vuông góc của đỉnh S trên mặt phẳng đáy là điểm H thuộc cạnh AB sao cho HB = 2HA . Biết SC tạo với đáy một góc 45° và cạnh bên SA = 2\[a\sqrt 2 \] . Tính khoảng cách từ điểm C đến mặt phẳng (SAB).
A. \[\frac{{a\sqrt 3 }}{2}\]
B. \[\frac{{2a\sqrt 2 }}{3}\]
C. \[\frac{{3a\sqrt 3 }}{2}\]
D. \[\frac{{a\sqrt 2 }}{3}\]
Câu 3. Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a, DSAB là tam giác vuông cân tại S nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ trung điểm H của AB đến mặt phẳng (SBD) là?
A. \[\frac{{a\sqrt 3 }}{3}\]
B. a
C. \[\frac{{a\sqrt 3 }}{2}\]
D. \[\frac{{a\sqrt {10} }}{2}\]
Câu 4. Cho hình chóp S.ABC có SA = 3a và SA ^ (ABC) . Biết AB = BC = 2a , ABC = 120° . Tính khoảng cách từ A đến (SBC) ?
A. 2a
B. \[\frac{a}{2}\]
C. a
D. \[\frac{{3a}}{2}\]
Câu 5. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AC = a\[\sqrt 3 \], ABC = = 30° , góc giữa SC và mặt phẳng ( ABC) bằng 60°. Cạnh bên S vuông góc với đáy. Khoảng cách từ A đến mặt phẳng (SBC) bằng
A. \[\frac{{a\sqrt 6 }}{{\sqrt {35} }}\]
B. \[\frac{{a\sqrt 3 }}{{\sqrt {35} }}\]
C. \[\frac{{3a}}{{\sqrt 5 }}\]
D. \[\frac{{2a\sqrt 3 }}{{\sqrt {35} }}\]
Câu 6. Cho hình lăng trụ ABC A’ B’ C’ có AB = a \[\sqrt 3 \], ABC = 30°, ACB = 60 °. Hình chiếu vuông góc của A’ trên mặt đáy là trung điểm của BC. Thể tích khối chóp A ABC ‘ bằng \[\frac{{{a^3}}}{6}\]. Khoảng cách từ C đến mặt phẳng ( A AB ‘ ) bằng
A. \[\frac{{a\sqrt 6 }}{6}\]
B. \[\frac{{2a}}{{\sqrt 7 }}\]
C. \[\frac{{a\sqrt 6 }}{4}\]
D. \[\frac{{a\sqrt 6 }}{{12}}\]
Câu 7. Cho hình chóp đều S.ABC có AB = a , góc giữa mặt bên và mặt đáy bằng 60°. Tính \[\frac{{4d}}{a}\] , biết d là khoảng cách từ điểm A đến mặt phẳng (SBC).
A. 3
B. 5
C. 7
D. 9
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ^ ( ABCD) , SA = AB = a và AD = x.a. Gọi E là trung điểm cạnh SC. Tìm x, biết khoảng cách từ điểm E đến mặt phẳng (SBD) là d = \[\frac{a}{3}\]
A. x =1
B. x = 2
C. x = 3
D. x = 4
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, SA ^ ( ABCD) , SA = \[a\sqrt 3 \] . Tính theo a khoảng cách từ điểm O đến mặt phẳng (SBC).
A. \[\frac{a}{2}\]
B. \[\frac{{a\sqrt 3 }}{4}\]
C. \[\frac{{a\sqrt 5 }}{6}\]
D. \[\frac{{a\sqrt 7 }}{8}\]
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ^ (ABCD) , SA = AB = a và AD = 2a . Gọi F là trung điểm cạnh CD. Tính \[\frac{{33d}}{a}\] , biết d là khoảng cách từ điểm A đến mặt phẳng (SBF) .
A. \[2\sqrt {33} \]
B. \[4\sqrt {33} \]
C. \[2\sqrt {11} \]
D. \[4\sqrt {11} \]
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 4a. Gọi H là điểm thuộc đường thẳng AB sao cho \[3\overrightarrow {HA} + \overrightarrow {HB} = 0\]. Hai mặt phẳng (SAB) và (SHC) đều vuông góc với mặt phẳng đáy. Tính khoảng cách từ B đến mặt phẳng (SHC).
A. \[\frac{{5a}}{{12}}\]
B. \[\frac{{5a}}{6}\]
C. \[\frac{{12a}}{5}\]
D. \[\frac{{6a}}{5}\]
Câu 12. Cho hình chóp đều S.ABCD có cạnh đáy bằng a. Gọi O là giao điểm của hai đường chéo, M là trung điểm của CD. Tính khoảng cách từ C đến mặt phẳng (SOM)
A. a
B. \[\frac{a}{2}\]
C. \[\frac{a}{4}\]
D. \[\frac{a}{8}\]
Câu 13. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Gọi O là giao điểm của hai đường chéo. Tính khoảng cách từ điểm O tới mặt phẳng (SHC) biết thể tích khối chóp S.ABCD là \[\frac{{{a^3}\sqrt 3 }}{3}\]
A. \[\frac{a}{{\sqrt {17} }}\]
B. \[\frac{{2a}}{{\sqrt {17} }}\]
C. \[\frac{a}{{\sqrt {27} }}\]
D. \[\frac{{2a}}{{\sqrt {27} }}\]
Câu 14. Cho hình hộp đứng ABCD A’B’C’D. có đáy là hình vuông, tam giác A’AC vuông cân tại A, cạnh A’C = 2a . Tính khoảng cách từ A đến mặt phẳng (BCD’) theo a?
A. \[\frac{{a\sqrt 3 }}{3}\]
B. \[\frac{{a\sqrt 6 }}{3}\]
C. \[\frac{{a\sqrt 2 }}{2}\]
D. \[\frac{{a\sqrt 3 }}{2}\]
Câu 15. Cho hình chóp S.ABC có SA = 3a và SA ^ (ABC) . Giả sử AB = BC = 2a, góc ABC = 120° . Tìm khoảng cách từ A đến mặt phẳng (SBC) ?
A. \[\frac{a}{2}\]
B. a
C. \[\frac{{3a}}{2}\]
D. 2a
Câu 16. Cho hình chóp S.ABC có đáy ABC là tam giác với AB = a, AC = 2a, BAC = 120°. Cạnh SA vuông góc với mặt phẳng đáy và (SBC) tạo với đáy một góc 60°. Khoảng cách từ điểm A đến mặt phẳng (SBC) là:
A. \[\frac{{3a}}{{2\sqrt 7 }}\]
B. \[\frac{{3\sqrt 7 a}}{2}\]
C. \[\frac{{a\sqrt 7 }}{2}\]
D. \[\frac{{2\sqrt 7 a}}{3}\]
Câu 17. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA vuông góc với mặt phẳng đáy. Cạnh SC hợp với đáy một góc 60°. Gọi h là khoảng cách từ điểm A đến mặt phẳng (SBD) . Tỉ số \[\frac{h}{a}\] bằng
A. \[\frac{{\sqrt {18} }}{{13}}\]
B. \[\frac{{\sqrt {78} }}{{13}}\]
C. \[\frac{{\sqrt {58} }}{{13}}\]
D. \[\frac{{\sqrt {38} }}{{13}}\]
Câu 18. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B; AD = 2AB = 2BC; BC = a; SA ^ (ABCD) và SB hợp với mặt phẳng đáy một góc 45°. Tính \[\frac{{d(A,(SDC))}}{a}\]
A. \[\frac{{2\sqrt 6 }}{3}\]
B. \[\frac{{2\sqrt 3 }}{3}\]
C. \[\frac{{\sqrt 2 }}{3}\]
D. \[\frac{{\sqrt 6 }}{3}\]
Câu 19. Cho hình chóp S.ABCD có đáy ABCD là hình thang ABC = BAD = 90° , BA = BC = a; AD = 2a. Cạnh bên SA vuông góc với đáy. Góc tạo bởi giữa SC và (SAD) bằng 30°. Tính khoảng cách từ A đến (SCD) .
A. a
B. \[a\sqrt 2 \]
C. \[\frac{a}{2}\]
D. \[a\sqrt 3 \]
Câu 20. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a có BAD = 120° . Cho SA ^ (ABCD) . Gọi M là trung điểm của BC; biết SMA = 45° . Tính d (B, (SDC))?
A. \[\frac{{a\sqrt 6 }}{4}\]
B. \[\frac{{a\sqrt 6 }}{2}\]
C. \[\frac{{a\sqrt 3 }}{2}\]
D. \[\frac{{a\sqrt 3 }}{8}\]
Hướng dẫn giải
Câu 1.

Chọn đáp án B
Ta có \[\left\{ {\begin{array}{*{20}{c}}{(SAC) \bot (ABC{\rm{D}})}\\{(SBD) \bot (ABC{\rm{D}})}\end{array}} \right.\]
Và (SAC) Ç (SBD) = SO
Þ SO ^ (ABCD) với O = AC Ç BD
Kẻ AH ^ BD ta có \[\left\{ {\begin{array}{*{20}{c}}{AH \bot BD}\\{AH \bot SO}\end{array}} \right. \Rightarrow AH \bot (SB{\rm{D}})\]
Ta có
\[\begin{array}{l}\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} = \frac{5}{{4{a^2}}} \Rightarrow AH = \frac{{2a}}{{\sqrt 5 }}\\ \Rightarrow d(A,(SBD)) = \frac{{2a}}{{\sqrt 5 }}\end{array}\]
Câu 2.
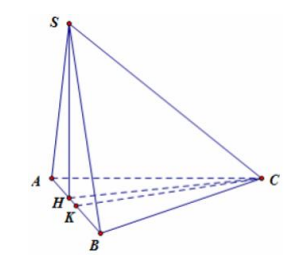
Chọn đáp án C
Ta có (SC,(ABC)) = SCH = 450
Giả sử AB = BC = CA = 3x
Ta có CH = \[\sqrt {A{H^2} + A{C^2} – 2AH.AC.c{\rm{os6}}{{\rm{0}}^0}} = x\sqrt 7 \]
Ta lại có SA2 = SH2 + AH2 Û 8a2 = 8x2 Û x = a
Þ AB = BC = CA = 3a
Kẻ CK ^ AB ta có \[\left\{ {\begin{array}{*{20}{c}}{CK \bot AB}\\{CK \bot SH}\end{array}} \right. \Rightarrow d(C,(SAB) = \frac{{3a\sqrt 3 }}{2}\]
Câu 3.
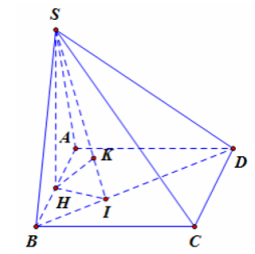
Chọn đáp án A
Vì DSAB là tam giác vuông cân tại S nên SH ^ (ABCD). Từ H kẻ HI ^ BD , từ H kẻ HK ^ SI với I Î BD, K Î SI. Ta có
\[\left\{ {\begin{array}{*{20}{c}}{SH \bot BD}\\{HI \bot BD}\end{array}} \right. \Rightarrow BD \bot (SHI) \Rightarrow BD \bot HK \Rightarrow HK \bot (SBD)\].
Do đó d(H,(SBD) = HK. Mặt khác \[\frac{1}{{H{I^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{K^2}}}\]
Mà HI = \[\frac{1}{2}d(A,BD) = \frac{a}{{\sqrt 2 }}\] và SH = \[\frac{{AB}}{2} = a.\]
Nên \[\frac{1}{2}d(A,BD) = \frac{1}{{H{K^2}}} = \frac{1}{{{{\left( {\frac{a}{{\sqrt 2 }}} \right)}^2}}} + \frac{1}{{{a^2}}} = \frac{3}{{{a^2}}} \Rightarrow HK = \frac{a}{{\sqrt 3 }}.\]
Câu 4.

Chọn đáp án D
Từ A kẻ AH ^ BC, kẻ AK ^ SH với H Î BC, K Î SH. Ta có
\[\left\{ {\begin{array}{*{20}{c}}{SA \bot BC}\\{AH \bot BC}\end{array}} \right. \Rightarrow BC \bot (SAH) \Rightarrow BC \bot AK \Rightarrow AK \bot (SBC)\]
Do đó d(A,(SBC) = AK thỏa mãn \[\frac{1}{{S{A^2}}} = \frac{1}{{A{H^2}}} + \frac{1}{{A{K^2}}}\]
Mà SA = 3a và AH = sin 600 .AB = \[\frac{{\sqrt 3 }}{2}.2a = a\sqrt 3 \]
Nên
\[\begin{array}{l}\frac{1}{{A{K^2}}} = \frac{1}{{9{a^2}}} + \frac{1}{{3{a^2}}} = \frac{4}{{9{a^2}}} \Rightarrow AK = \frac{{3a}}{2}\\ \Rightarrow d(A,(SBC)) = \frac{{3a}}{2}\end{array}\]
Câu 5.
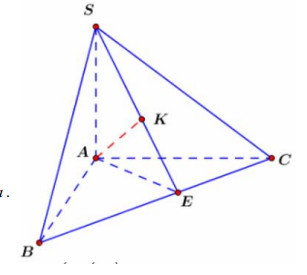
Chọn đáp án C
Kẻ AE ^ BC, AK ^ SE, (E Î BC, K Î SE). Chứng minh AK ^ (SBC) Þ AK = d (A, (SBC). Xét tam giác SAE vuông tại A ta có:
\[AK = \frac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }}\]
Tính SA, AE:
Xét hai tam giác vuông ABC và SAC: AB = SA = 3a.
Xét tam giác vuông ABC: AE = \[\frac{{3a}}{2}\].
Þ d(A,(SBC)) = HK = \[\frac{{3a}}{{\sqrt 5 }}\].
Xem thêm