Giải SBT Toán 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Bài 68 trang 34 SBT Toán 12 Tập 1: Đồ thị hàm số y = 4x3 – 6x2 + 1 là đường cong nào trong các đường cong sau?
A.
B.
C.
D.
Lời giải:
Đáp án đúng là: A
Do hệ số của x3 trong hàm số đã cho là a = 4 > 0 nên đồ thị hàm số có thể là phương án A hoặc C.
Mặt khác khi thay x = 1 vào hàm số y = 4x3 – 6x2 + 1 ta được y = −1 tức là đồ thị hàm số đi qua điểm có tọa độ (1; −1).
Vậy phương án đúng là A.
Bài 69 trang 34 SBT Toán 12 Tập 1: Đồ thị hàm số y = −x3 – x + 2 là đường cong nào trong các đường cong sau?
A.
B.
C.
D.
Lời giải:
Đáp án đúng là: D
Do hệ số của x3 trong hàm số là a = −1 < 0 nên đồ thị hàm số có thể là phương án B hoặc D.
Mặt khác y’ = −3x2 – 1 < 0 với ∀x nên đồ thị hàm số không có điểm cực trị.
Vậy phương án đúng là D.
Bài 70 trang 35 SBT Toán 12 Tập 1: Đồ thị hàm số y = là đường cong nào trong các đường cong sau?
A.
B.
C.
D.
Lời giải:
Đáp án đúng là: D
Ta có: y = .
Tập xác định: D = ℝ\{−1}.
Có y’ = > 0 với ∀x ∈ D.
Hàm số đồng biến trên mỗi khoảng (−∞; −1) và (−1; +∞) nên trên mỗi khoảng này đồ thị hàm số đi lên từ trái qua phải, do đó phương án đúng là D.
Bài 71 trang 35 SBT Toán 12 Tập 1: Đồ thị hàm số y = là đường cong nào trong các đường cong sau?
A.
B.
C.
D.
Lời giải:
Đáp án đúng là: B
Ta có: y =
Tập xác định: D = ℝ\{−1}.
Đồ thị hàm số này có đường tiệm cận đứng x = −1 nên có thể là phương án B hoặc D.
Có hệ số của x2 ở tử là a = 1 và hệ số của x ở mẫu là m = 1 nên a, m cùng dấu.
Vậy phương án đúng là B.
Bài 72 trang 36 SBT Toán 12 Tập 1: Đường cong ở Hình 16 là đồ thị của hàm số:
A. y = + x2 – 4.
B. y = x3 – 3x2 – 4.
C. y = x3 + 3x2 – 4.
D. y = −x3 – 3x2 + 4.
Lời giải:
Đáp án đúng là: C
Dựa vào đồ thị hàm số ở Hình 16, ta có:
Hệ số a > 0 nên phương án có thể là B hoặc C.
Đồ thị hàm số đi qua điểm (−2; 0).
Khi thay x = −2 vào phương án B được y = (−2)3 – 3.(−2)2 – 4 = −24 ≠ 0 nên phương án B loại.
Vậy phương án đúng là C.
Bài 73 trang 36 SBT Toán 12 Tập 1: Đường cong ở Hình 17 là đồ thị của hàm số:
A. y =
B. y =
C. y =
D. y =
Lời giải:
Đáp án đúng là: A
Dựa vào đồ thị hàm số ở Hình 17, ta có:
Đồ thị hàm số có tiệm cận đứng là đường thẳng x = 2 nên ta loại phương án D.
Đồ thị hàm số có tiệm cận ngang là đường thẳng y = −1 nên ta loại phương án C.
Với x = 1 thì y = nên đồ thị hàm số y = đi qua điểm (1; 0), mà đồ thị hàm số trong Hình 17 không đi qua điểm (1; 0) nên ta loại phương án B.
Vậy phương án đúng là A.
Bài 74 trang 36 SBT Toán 12 Tập 1: Đường cong ở Hình 18 là đồ thị của hàm số:
A. y =
B. y =
C. y =
D. y =
Lời giải:
Đáp án đúng là: D
Dựa vào đồ thị hàm số ở Hình 18, ta có:
Đồ thị hàm số có tiệm cận xiên là đường thẳng đi xuống từ trái qua phải nên hệ số a, m trái dấu, loại phương án A.
Đồ thị hàm số đi qua điểm (2; 0) nên ta loại phương án B.
Đồ thị hàm số ở phương án C có tiệm cận xiên là đường thẳng y = .
Đồ thị hàm số ở phương án D có tiệm cận xiên là đường thẳng y = −x + 1.
Nhận thấy đồ thị hàm số ở Hình 18 có đường tiệm cận xiên đi qua hai điểm (0; 1) và (1; 0) nên phương án D thỏa mãn.
Vậy phương án đúng là D.
Bài 75 trang 36 SBT Toán 12 Tập 1: Cho hàm số y = với a > 0 có đồ thị là đường cong ở Hình 19. Mệnh đề nào dưới đây là đúng?
A. b > 0, c < 0, d < 0.
B. b > 0, c > 0, d < 0.
C. b < 0, c > 0, d < 0.
D. b < 0, c < 0, d < 0.
Lời giải:
Đáp án đúng là: B
Ta có: y = và a > 0.
Căn cứ vào đồ thị hàm số Hình 19, ta có:
Đồ thị hàm số y = có đường tiệm cận ngang y = > 0 tức là a, c cùng dấu nên c > 0.
Đồ thị hàm số y = có đường tiệm cận đứng x = > 0 hay < 0 tức là d, c trái dấu nên d < 0.
Khi y = 0 ta được x = < 0 hay > 0 tức là b, a cùng dấu nên b > 0.
Vậy ta có b > 0, c > 0, d < 0.
Bài 76 trang 37 SBT Toán 12 Tập 1: Cho hàm số y = ax3 + bx2 + cx + d (a ≠ 0) có đồ thị là đường cong ở Hình 20.
|
a) a > 0. |
|
|
|
b) Đồ thị cắt trục tung tại điểm có tung độ dương. |
|
|
|
c) Đồ thị hàm số có hai điểm cực trị nằm cùng phía với trục tung. |
|
|
|
d) b < 0. |
|
|
Lời giải:
|
a) Đ |
b) Đ |
c) S |
d) S |
Căn cứ vào hình dáng của đồ thị hàm số, ta có a > 0.
Đồ thị cắt trục tung tại điểm (0; d) nằm phía trên trục hoành nên điểm này có tung độ dương.
Đồ thị hàm số có hai điểm cực trị nằm ở hai phía trục tung.
Ta có: y = ax3 + bx2 + cx + d ⇒y’ = 3ax2 + 2bx + c
Hàm số có hai cực trị nên y’ = 0 có hai nghiệm phân biệt x1, x2.
Theo Viet ta có: x1 + x2 = .
Ta thấy trung điểm đoạn nối hai điểm cực trị x1, x2 nằm về phía bên phải trục tung nên tổng hai điểm cực trị x1, x2 dương hay > 0.
Mà a > 0 nên b < 0.
Bài 77 trang 37 SBT Toán 12 Tập 1: Cho hàm số y = có đồ thị là đường cong ở Hình 21.
|
a) n < 0. |
|
|
|
b) a > 0. |
|
|
|
c) c > 0. |
|
|
|
d) b < 0. |
|
|
Lời giải:
|
a) S |
b) Đ |
c) Đ |
d) S |
Tiệm cận đứng của đồ thị hàm số là đường thẳng x = −n nằm bên trái trục tung nên
−n < 0 hay n > 0.
Tiệm cận xiên có hệ số góc là a có hướng đi lên từ trái sang phải nên a > 0.
Đồ thị cắt trục tung tại điểm (0;) nằm về phía trên trục hoành nên c > 0.
Đồ thị cắt trục hoành tại hai điểm có hoành độ âm nên phương trình ax2 + bx + c = 0 có hai nghiệm âm phân biệt nên < 0 hay b > 0.
Bài 78 trang 37 SBT Toán 12 Tập 1: Cho hàm số bậc ba y = f(x) = ax3 + bx2 + cx + d có đồ thị là đường cong như Hình 22.
Căn cứ vào đồ thị hàm số:
a) Tìm khoảng đơn điệu, điểm cực đại, cực tiểu của hàm số.
b) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [−1; 2].
c) Tìm điểm trên đồ thị hàm số có hoành độ bằng 2.
d) Tìm điểm trên đồ thị hàm số có tung độ bằng 2.
e) Đường thẳng y = 1 cắt đồ thị hàm số y = f(x) tại mấy điểm?
g) Với giá trị nào của x thì −2 < f(x) < 2.
h) Tìm công thức xác định hàm số f(x).
Lời giải:
a) Dựa vào đồ thị Hình 22, ta có:
Hàm số đồng biến trên các khoảng (−∞; 0) và (2; +∞).
Hàm số nghịch biến trên khoảng (0; 2).
Hàm số đạt cực đại tại x = 0, đạt cực tiểu tại x = 2.
b) Trên đoạn [−1; 2], hàm số đạt giá trị lớn nhất bằng 2 tại x = 0, hàm số đạt giá trị nhỏ nhất bằng −2 tại x = 2, x = −1.
c) Điểm thỏa mãn là: (2; −2).
d) Điểm thỏa mãn là: (0; 2) và (3; 2).
e) Đường thẳng y = 1 cát đồ thị hàm số y = f(x) tại ba điểm.
g) Để −2 < f(x) < 2 thì x ∈ (−1; 3)\{0; 2}.
h) Hàm số y = f(x) = ax3 + bx2 + cx + d
Hàm số đi qua điểm (0; 2) nên d = 2.
Hàm số đi qua điểm (2; −2) nên 8a + 4b + 2c + 2 = −2 hay 4a + 2b + c = −2 (1).
Hàm số đi qua điểm (3; 2) nên 27a + 9b + 3c + 2 = 2 hay 9a + 3b + c = 0 (2).
Hàm số đi qua điểm (−1; −2) nên −a + b – c + 2 = −2 hay −a + b – c = −4 (3).
Từ (1), (2), (3) ta có hệ phương trình:
Vậy y = f(x) = x3 – 3x2 + 2.
Bài 79 trang 38 SBT Toán 12 Tập 1: Cho hàm số y = f(x) = với (a, m ≠ 0) có đồ thị là đường cong như Hình 23.
Căn cứ vào đồ thị hàm số:
a) Tìm khoảng đơn điệu, điểm cực đại, cực tiểu của hàm số.
b) Viết phương trình đường tiệm cận đứng, tiệm cận xiên của đồ thị hàm số.
c) Phương trình f(x) = 3 có bao nhiêu nghiệm?
d) Tìm công thức xác định hàm số y = f(x), biết m = 1.
Lời giải:
Dựa vào đồ thị hàm số Hình 23, ta thấy:
a) Hàm số đồng biến trên các khoảng (−∞; −3) và (−1; +∞).
Hàm số nghịch biến trên các khoảng (−3; −2) và (−2; −1).
Điểm cực đại x = −3, điểm cực tiểu x = −1.
b) Tiệm cận đứng của đồ thị hàm số có phương trình x = −2.
Tiệm cận xiên của đồ thị hàm số các điểm (−2; −1); (−1; 0) và (0; 1).
Gọi phương trình đường tiệm cận xiên của đồ thị hàm số y = hx + k (h ≠ 0).
Ta có:
Vậy tiệm cận xiên của đồ thị hàm số có phương trình: y = x + 1.
c) Số nghiệm của phương trình f(x) = 3 là số giao điểm của đồ thị hàm số f(x) và đường thẳng y = 3. Căn cứ vào đồ thị hàm số, phương trình f(x) = 3 có hai nghiệm phân biệt.
d) Ta có: y = f(x) =
Với m = 1, f(x) = .
Đồ thị hàm số có tiệm cận đứng x = −2 nên n = 2.
Lúc này, ta có: f(x) = .
Thực hiện phép chia đa thức lấy tử (ax2 + bx + c) chia cho mẫu (x + 2) ta được thương là ax + b – 2a chính là phương trình đường tiệm cận xiên.
⇒ ax + b – 2a = x + 1 ⇒ hay
.
⇒f(x) = .
Đồ thị hàm số đi qua điểm (−3; −3) nên ta có: = −3 ⇒ c = 3.
Vậy y = f(x) = .
Bài 80 trang 38 SBT Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:
a) y = (x – 2)(x + 1)2;
b) y = x3 – x2 + 2;
c) y = 2x3 – 3x2 + 2x – 1;
d) y = (x3 – 6x2 + 12x).
Lời giải:
a) y = (x – 2)(x + 1)2
1) Tập xác định: D = ℝ.
2) Sự biến thiên.
Giới hạn tại vô cực: y = +∞, y = −∞.
Ta có: y’ = 3x2 – 3.
y’ = 0 khi x = ±1.
Ta có bảng biến thiên như sau:
Hàm số nghịch biến trên khoảng (−1; 1).
Hàm số đồng biến trên các khoảng (−∞; −1) và (1; +∞).
Hàm số đạt cực tiểu tại x = 1, yCT = −4; hàm số đạt cực đại tại x = −1, yCĐ = 0.
3) Đồ thị
Giao điểm của đồ thị với trục tung là (0; −2).
Đồ thị hàm số đi qua các điểm (−1; 0); (0; −2); (1; −4); (2; 0); (−2; −4).
Ta có đồ thị:
b) y = x3 – x2 + 2
1) Tập xác định: D = ℝ.
2) Sự biến thiên.
Giới hạn tại vô cực: y = −∞, y = +∞.
Ta có: y’ = −x2 – 2x.
y’ = 0 khi x = 0 hoặc x = −2.
Ta có bảng biến thiên như sau:
Hàm số đồng biến trên khoảng (−2; 0).
Hàm số nghịch biến trên các khoảng (−∞; −2) và (0; +∞).
Hàm số đạt cực tiểu tại x = −2, yCT = ; hàm số đạt cực đại tại x = 0, yCĐ = 2.
3) Đồ thị
Giao điểm của đồ thị với trục tung là (0; 2).
Đồ thị hàm số đi qua các điểm ; (0; 2); ; (−3; 2); .
Ta có đồ thị hàm số:
c) y = 2x3 – 3x2 + 2x – 1
1) Tập xác định: D = ℝ.
2) Sự biến thiên.
Giới hạn tại vô cực: y = +∞, y = −∞.
Ta có: y’ = 6x2 – 6x + 2.
y’ = 6(x2 – x + ) = 6(x − )2 + > 0 với mọi x.
Hàm số đồng biến trên ℝ.
Ta có bảng biến thiên như sau:
3) Đồ thị
Giao điểm của đồ thị với trục tung là (0; −1).
Đồ thị hàm số đi qua các điểm: (−1; −8); (0; −1); (1; 0); ; (2; 7).
Ta có đồ thị như sau:
d) y = (x3 – 6x2 + 12x)
hay y = x3 + x2 – 3x.
1) Tập xác định: D = ℝ.
2) Sự biến thiên.
Giới hạn tại vô cực: y = −∞, y = +∞.
Ta có: y’ = x2 + 3x – 3 = 3(− x2 + x − 1);
y’ = 0 ⇔ − x2 + x − 1 = 0
⇔ −x2 + 4x − 4 = 0
⇔ −(x – 2)2 = 0
⇔ x = 2 (nghiệm kép).
Ta có bảng biến thiên:
Hàm số nghịch biến trên ℝ.
3) Đồ thị
Đồ thị hàm số đi qua các điểm: ; (0; 0); ; (2; −2); ; (4; −4).
Ta có đồ thị của hàm số như sau:
Bài 81 trang 38 SBT Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:
a) y = ;
b) y = ;
c) y = ;
d) y = .
Lời giải:
a) y =
1) Tập xác định: D = ℝ\{−1}.
2) Sự biến thiên.
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận.
Ta có: y = 2, y = 2.
Do đó, đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
y = +∞, y = −∞.
Do đó, đường thẳng x = −1 là tiệm cận đứng của đồ thị hàm số.
Ta có: y’ = > 0, với ∀x ∈ D.
Ta có bảng biến thiên như sau:
Hàm số đồng biến trên các khoảng (−∞; −1) và (−1; +∞).
3) Đồ thị:
Đồ thị hàm số nhận đường thẳng x = −1 là tiệm cận đứng, y = 2 là tiệm cận ngang.
Giao của đồ thị với trục tung tại điểm (0; −1), giao của đồ thị với trục hoành tại điểm .
Đồ thị hàm số đi qua các điểm: (−4; 3); (−2; 5); (2; 1); ; (0; −1).
Ta có đồ thị như sau:
Đồ thị hàm số nhận giao điểm của hai đường tiệm cận có tọa độ (−1; 2) làm tâm đối xứng và nhận phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
b) y =
1) Tập xác định: D = ℝ\{2}.
2) Sự biến thiên.
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận.
Ta có: y = 1, y = 1.
Do đó, đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
y = −∞, y = +∞.
Do đó, đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
Ta có: y’ = < 0, với ∀x ∈ D.
Ta có bảng biến thiên như sau:
Hàm số nghịch biến trên các khoảng (−∞; 2) và (2; +∞).
3) Đồ thị
Đồ thị hàm số nhận đường thẳng x = 2 làm tiệm cận đứng và y = 1 làm tiệm cận ngang.
Đồ thị hàm số đi qua các điểm: (0; 0); ; (1; – 1) (3; 3); (4; 2).
Ta có đồ thị hàm số như sau:
Đồ thị nhận giao điểm của hai đường tiệm cận có tọa độ (2; 1) làm tâm đối xứng và nhận phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
c) y =
1) Tập xác định: D = ℝ\{1}.
2) Sự biến thiên.
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận.
Ta có: y = −∞, y = +∞.
y = +∞, y = −∞.
Do đó, đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
= = = −1.
[y – (−x)] = = = 1.
Do đó, đường thẳng y = −x + 1 là tiệm cận xiên của đồ thị hàm số.
Ta có: y’ =
y’ = 0 ⇔ = 0 ⇔ x = 0 hoặc x = 2.
Ta có bảng biến thiên như sau:
Hàm số nghịch biến trên các khoảng (−∞; 0) và (2; +∞).
Hàm số đồng biến trên các khoảng (0; 1) và (1; 2).
Hàm số đạt cực tiểu tại x = 0, yCT = 2; hàm số đạt cực đại tại x = 2, yCĐ = −2.
3) Đồ thị
Đồ thị hàm số nhận đường thẳng x = 1 làm tiệm cận đứng và y = −x + 1 làm tiệm cận xiên.
Giao của đồ thị hàm số với trục tung là (0; 2).
Hàm số đi qua các điểm: ; ; (0; 2); (2; −2); .
Ta có đồ thị hàm số:
Đồ thị hàm số nhận giao điểm của hai đường tiệm cận có tọa độ (1; 0) làm tâm đối xứng và nhận phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
d) y =
1) Tập xác định: D = ℝ\{−2}.
2) Sự biến thiên.
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận.
Ta có: y = +∞, y = −∞.
y = +∞, y = −∞.
Do đó, đường thẳng x = – 2 là tiệm cận đứng của đồ thị hàm số.
= = = 1.
(y – x) = = = 0.
Do đó, đường thẳng y = x là tiệm cận xiên của đồ thị hàm số.
Ta có: y’ = = > 0, với ∀x ∈ D.
Ta có bảng biến thiên như sau:
Hàm số đồng biến trên các khoảng (−∞; −2) và (−2; +∞).
3) Đồ thị
Đồ thị hàm số nhận đường thẳng x = − 2 làm tiệm cận đứng và y = x làm tiệm cận xiên.
Giao của đồ thị với trục tung tại điểm ; giao của đồ thị với trục hoành tại các điểm (1; 0); (−3; 0).
Đồ thị hàm số đi qua các điểm: ; (1; 0); (−3; 0); (−1; −4); (−5; −4);
Ta có đồ thị như sau:
Đồ thị hàm số nhận giao điểm của hai đường tiệm cận có tọa độ (−2; −2) làm tâm đối xứng và nhận phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
Bài 82* trang 38 SBT Toán 12 Tập 1: Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó gắn với hệ trục tọa độ Oxy với mô phỏng ở Hình 24. Biết đường bay của nó có dạng đồ thị hàm số bậc ba; vị trí bắt đầu hạ cánh có tọa độ (−4; 1) là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc tọa độ là điểm cực tiểu của đồ thị hàm số.
a) Tìm công thức xác định hàm số mô phỏng đường bay của máy bay trên đoạn [−4; 0].
b) Khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay bay cách mặt đất bao nhiêu dặm? (Biết đơn vị trên hệ trục tọa độ là dặm).
c) Khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang bao nhiêu dặm?
Lời giải:
a) Gọi hàm số mô phỏng đường bay của máy bay trên đoạn [−4; 0] là:
y = ax3 + bx2 + cx + d (a ≠ 0).
y’ = 3ax2 + 2bx + c
Hàm số đi qua các điểm (−4; 1), (0; 0).
Đi qua điểm (0; 0) nên d = 0.
Đi qua điểm (−4; 1) nên −64a + 16b – 4c = 1 (1).
Theo đề: (−4; 1) là điểm cực đại của đồ thị hàm số và (0; 0) là điểm cực tiểu của đồ thị hàm số nên: y'(−4) = 0 và y'(0) = 0.
⇒ 48a − 8b + c = 0 (2) và c = 0 (3).
Từ (1), (2), (3) suy ra
Vậy y = x3 + x2.
b) Thay x = −3 vào y = x3 + x2 ta được y = .
Vậy khi máy bay bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất = 0,84375 (dặm).
c) Thay y = 0,5 ta được phương trình:
x3 + x2 = 0,5 có nghiệm x = −2, x = −2 ± .
Do x ∈ [−4; 0] nên x = −2 thỏa mãn.
Vậy khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang 2 dặm.
Lý thuyết Khảo sát sự biến thiên và vẽ đồ thị của hàm số
1. Sơ đồ khảo sát hàm số
Các bước khảo sát hàm số
|
1. Tìm tập xác định của hàm số 2. Xét sự biến thiên của hàm số – Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số (nếu có) – Lập BBT của hàm số bao gồm: Tính đạo hàm của hàm số, xét dấu đạo hàm, xét chiều biến thiên và tìm cực trị của hàm số (nếu có), điền các kết quả vào bảng 3. Vẽ đồ thị của hàm số – Vẽ các đường tiệm cận (nếu có) – Xác định các điểm đặc biệt của đồ thị: cực trị, giao điểm của đồ thị với các trục tọa độ (trong trường hợp đơn giản), … – Nhận xét về đặc điểm của đồ thị: chỉ ra tâm đối xứng, trục đối xứng (nếu có) |
2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số bậc ba
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
1. Tập xác định của hàm số: R
2. Sự biến thiên:
Ta có: . Vậy y’ = 0 khi x = 0 hoặc x = 2
Trên khoảng , y’ > 0 nên hàm số đồng biến. Trên các khoảng và , y’ < 0 nên hàm số nghịch biến trên mỗi khoảng đó
Hàm số đạt cực tiểu tại x = 0, giá trị cực tiểu . Hàm số đạt cực đại tại x = 2, giá trị cực đại
Giới hạn tại vô cực:
BBT:

4. Đồ thị:
Giao điểm của đồ thị hàm số với trục tung là điểm
Ta có: y = 0 x = -1 hoặc x = 2. Do đó giao điểm của đồ thị hàm số với trục hoành là các điểm và
Đồ thị hàm số có tâm đối xứng là điểm
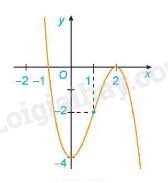
3. Khảo sát và vẽ đồ thị hàm số phân thức hữu tỷ
a) Hàm số phân thức
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
1. Tập xác định của hàm số: R\{2}
2. Sự biến thiên:
Ta có: với mọi
Hàm số nghịch biến trên từng khoảng và
Hàm số không có cực trị
Tiệm cận:
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận ngang là y = 1
BBT:
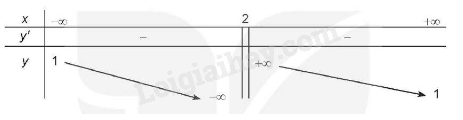
4. Đồ thị:
Giao điểm của đồ thị hàm số với trục tung là điểm
Giao điểm của đồ thị hàm số với trục hoành là điểm
Đồ thị hàm số nhận giao điểm I của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng
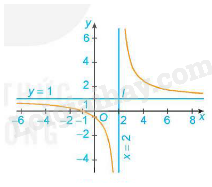
b) Hàm số phân thức (đa thức tử không chia hết cho đa thức mẫu)
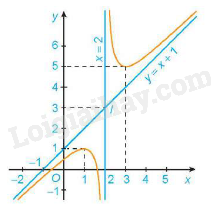
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
1. Tập xác định của hàm số: R\{2}
2. Sự biến thiên: Viết
Ta có: . Vậy y’ = 0 x = 1 hoặc x = 3
Trên các khoảng và , y’ > 0 nên hàm số đồng biến trên từng khoảng này
Trên các khoảng và , y’ < 0 nên hàm số nghịch biến trên từng khoảng này
Hàm số đạt cực đại tại x = 1 với ; hàm số đạt cực tiểu tại x = 3 với
;
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận xiên là y = x+1
BBT:
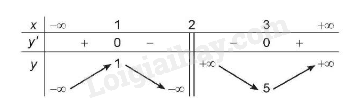
3. Đồ thị:
Giao điểm của đồ thị hàm số với trục tung là điểm
Ta có: . Do đó giao điểm của đồ thị hàm số với trục hoành là điểm
Đồ thị hàm số nhận giao điểm I của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng
4. Ứng dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn
Ví dụ: Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức (f(t) được tính bằng nghìn người)
a) Tính số dân của thị trấn vào năm 2022
b) Xem y = f(t) là một hàm số xác định trên nửa khoảng . Khảo sát sự biến thiên và vẽ đồ thị của hàm số f(t)
c) Đạo hàm của hàm số y = f(t) biểu thị tốc độ tăng dân số của thị trấn (tính bằng nghìn người/năm)
- Tính tốc độ tăng dân số vào năm 2022 của thị trấn đó
- Vào năm nào thì tốc độ tăng dân số là 0,192 nghìn người/năm ?
Giải:
a) Ta có: (nghìn người)
Vậy số dân của thị trấn vào năm 2022 khoảng 23895 nghìn người
b) 1) Sự biến thiên
- Giới hạn tại vô cực và đường tiệm cận ngang:
. Do đó, đường thẳng y = 26 là tiệm cận ngang của đồ thị hàm số.
- BBT:
với mọi

Hàm số đồng biến trên nửa khoảng .
Hàm số không có cực trị
2) Đồ thị
- Giao điểm của đồ thị với trục tung (0;2)
- Đồ thị hàm số đi qua điểm (1;6). Vậy đồ thị hàm số , được cho ở hình vẽ sau
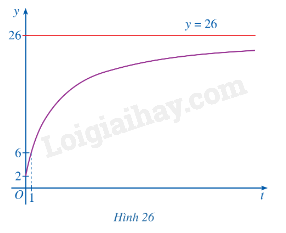
c)
- Tốc độ tăng dân số vào năm 2022 của thị trấn đó là:
- Ta có:
(do )
Vậy vào năm 1990, tốc độ tăng dân số là 0,192 nghìn người/năm
Xem thêm các bài giải SBT Toán lớp 12 Cánh diều hay, chi tiết khác:
Bài 3: Đường tiệm cận của đồ thị hàm số
Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Bài tập cuối chương 1
Bài 1: Vectơ và các phép toán vectơ trong không gian
Bài 2: Toạ độ của vectơ
Bài 3: Biểu thức toạ độ của các phép toán vectơ