Giải bài tập Toán lớp 12 Ôn tập chương IV – Số phức
Câu hỏi và bài tập (trang 143, 144 SGK Giải tích 12)
Câu 1 trang 143 SGK Giải tích 12: Thế nào là phần thực, phần ảo, modun của số phức?
Viết công thức tính môdun của một số phức theo phần thực và phần ảo của nó.
Lời giải:
– Mỗi biểu thức dạng , trong đó được gọi là một số phức.
– Với số phức , ta gọi là phần thực, số gọi là phần ảo của .
– Ta có thì môdun của là .
Câu 2 trang 143 SGK Giải tích 12: Tìm mối liên hệ giữa khái niệm môdun và khái niệm giá trị tuyệt đối của một số thực.
Phương pháp giải:
Môđun của mọi số phức là
Lời giải:
Nếu số phức là một số thực thì phần ảo của nó bằng 0, hay
Khi đó mô đun của là:
Vậy nếu là một số thực, thì môdun của chính là giá trị tuyệt đối của .
Câu 3 trang 143 SGK Giải tích 12: Nêu định nghĩa số phức liên hợp của số phức . Số phức nào bằng số phức liên hợp của nó?
Phương pháp giải:
Lời giải:
*Cho số phức . ()
Ta gọi số phức là số phức liên hợp của và kí hiệu là .
Vậy ta có thì
Vậy khi đó là một số thực.
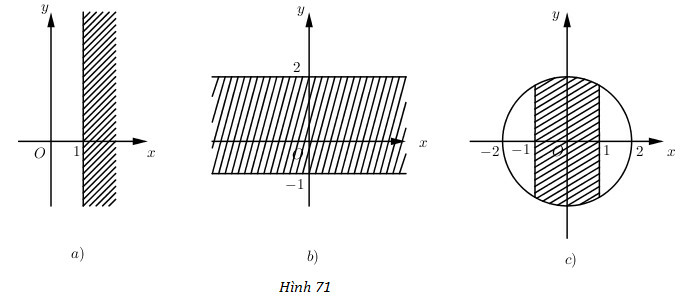
Câu 4 trang 143 SGK Giải tích 12: Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình 71 a), b), c) ?
Phương pháp giải:
Gọi số phức có dạng , (), khi đó số phức được biểu diễn bởi điểm trên mặt phẳng tọa độ .
Tìm miền giá trị của ở từng ý và nhận xét về số phức .
Lời giải:
Giả sử (), khi đó số phức được biểu diễn bởi điểm trên mặt phẳng tọa độ .
a) Tập hợp điểm M biểu diễn cho số phức thuộc phần gạch chéo là .
Vậy số phức thỏa mãn là với .
b) Tập hợp điểm M biểu diễn cho số phức thuộc phần gạch chéo là
Vậy số phức thỏa mãn là với .
c) Tập hợp điểm M biểu diễn cho số phức thuộc phần gạch chéo là .
Vậy số phức cần tìm có phần thực thuộc đoạn và môdun không vượt quá .
Câu 5 trang 143 SGK Giải tích 12: Trong mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức thỏa mãn điều kiện:
a) phần thực của bằng
b) phần ảo của bằng
c) Phần thực của thuộc đoạn , phần ảo của thuộc đoạn
d)
Phương pháp giải:
Điểm trên mặt phẳng tọa độ là điểm biểu diễn cho số phức .
Tìm điều kiện của và biểu diễn tập hợp điểm M trên mặt phẳng tọa độ.
Lời giải:
a)
Ta có tùy ý nên tập hợp các điểm biểu diễn là đường thẳng .
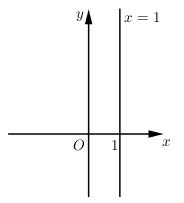
b)
Ta có tùy ý nên tập hợp các điểm biểu diễn là đường thẳng .

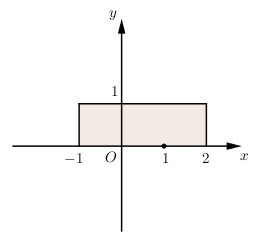
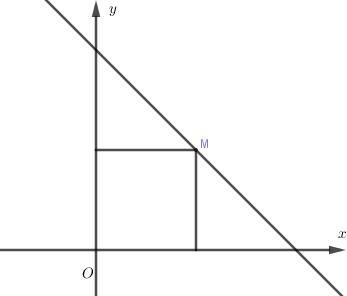
c)
Ta có , tức là , tập hợp các điểm M nằm bên trái đường thẳng và nằm bên phải đường thẳng và , tức là tập hợp các điểm M nằm bên dưới đường thẳng và nằm bên trên đường thẳng .
Vậy tập hợp các điểm biểu diễn là hình chữ được tô màu.
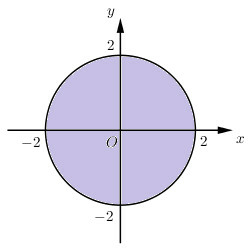
d)
Ta có:
Vậy tập hợp các điểm biểu diễn là hình tròn tâm (gốc tọa độ) bán kính bằng (kể cả các điểm trên đường tròn).
Câu 6 trang 143 SGK Giải tích 12: Tìm các số thực sao cho:
a)
b)
Phương pháp giải:
Lời giải:
a)
Vậy .
b)
Vậy
Câu 7 trang 143 SGK Giải tích 12: Chứng tỏ rằng với mọi số phức , ta luôn có phần thực và phần ảo của không vượt quá môdun của nó.
Phương pháp giải:
Gọi , so sánh với và với
Lời giải:
Giả sử
Khi đó:
Từ đó suy ra:
Câu 8 trang 143 SGK Giải tích 12: Thực hiện các phép tính sau:
a)
b)
c)
d)
Phương pháp giải:
Thực hiện các phép tính theo đúng thứ tự nhân, chia trước, công trừ sau, trong ngoặc trước, ngoài ngoặc sau.
Lời giải:
a)
b)
c)
d)
Câu 9 trang 144 SGK Giải tích 12: Giải các phương trình sau trên tập số phức:
a)
b)
Phương pháp giải:
+ Đưa phương trình về dạng
+ Giải phương trình dạng
Lời giải:
a)
b)
Câu 10 trang 144 SGK Giải tích 12: Giải các phương trình sau trên tập số phức
a)
b)
c)
Phương pháp giải:
a) Tính . Gọi là 1 căn bậc hai của , khi đó phương trình có 2 nghiệm:
b, c) Đặt , đưa phương trình về dạng phương trình bậc hai và giải phương trình bậc hai đó, khi đó nghiệm là căn bậc hai của các nghiệm tìm được ở trên
Lời giải:
a)
có
Căn bậc hai của là
Vậy phương trình có hai nghiệm là:
b)
Đặt , ta được phương trình :
Vậy phương trình đã cho có 4 nghiệm là:
c)
Đặt , ta được phương trình : .
Vậy phương trình đã cho có 4 nghiệm là và
Câu 11 trang 144 SGK Giải tích 12: Tìm hai số phức, biết tổng của chúng bằng và tích của chúng bằng .
Phương pháp giải:
Nếu thì là nghiệm của phương trình .
Lời giải:
Giả sử hai số cần tìm là và .
Ta có: ;
Rõ ràng, là các nghiệm của phương trình:
Phương trình có .
Căn bậc hai của là .
Vậy hai số phức cần tìm là:
Câu 12 trang 144 SGK Giải tích 12: Cho hai số phức . Biết rằng và là hai số thực. Chứng minh rằng là hai nghiệm của một phương trình bậc hai với hệ số thực.
Phương pháp giải:
Đặt ; . Khi đó là nghiệm của phương trình .
Lời giải:
Đặt ;
Khi đó, và là hai nghiệm của phương trình
Đó là phương trình bậc hai đối với hệ số thực. Suy ra điều phải chứng minh.
Bài tập trắc nghiệm (trang 144 SGK Giải tích 12)
Câu 1 trang 144 SGK Giải tích 12: Số nào trong các số sau là số thực?
A.
B.
C.
D.
Phương pháp giải:
Số phức là số thực nếu phần ảo của nó bằng .
Lời giải:
Ta tìm phần ảo của các số đã cho:
(A).
là số thuần ảo (loại A)
(B). là số thực.
(C). không là số thực.
(D). không là số thực.
Chọn đáp án (B)
Câu 2 trang 144 SGK Giải tích 12: Số nào trong các số sau là số thuần ảo?
A.
B.
C.
D.
Phương pháp giải:
Số thuần ảo là số phức có phần thực bằng .
Lời giải:
Ta tìm phần thực của các số đã cho:
(A) là số thực.
(B) là số thực.
(C) là số thuần ảo.
(D) không là số thuần ảo.
Chọn đáp án (C)
Câu 3 trang 144 SGK Giải tích 12: Đẳng thức nào trong các đẳng thức sau là đúng?
A. B.
C. D.
Phương pháp giải:
Sử dụng kết quả đã chứng minh ở bài 4 – SGK trang 136
Lời giải:
Ta có:
Chọn đáp án (B)
Câu 4 trang 144 SGK Giải tích 12: Đẳng thức nào trong các đẳng thức sau là đúng?
A.
B.
C.
D.
Phương pháp giải:
Tính , sau đó tính , sau đó .
Lời giải:
Chọn đáp án C
Câu 5 trang 144 SGK Giải tích 12: Biết rằng nghịch đảo của số phức bằng số phức liên hợp của nó, trong các kết luận sau, kết luận nào là đúng?
A. B.
C. là một số thuần ảo D.
Phương pháp giải:
Sử dụng công thức
Lời giải:
Ta có:
Chọn đáp án (B)
Câu 6 trang 144 SGK Giải tích 12: Trong các kết luận sau, kết luận nào là sai?
A. Môdun của số phức là một số thực
B. Môdun của số phức là một số phức
C. Môdun của số phức là một số thực dương
D. Môdun của số phức là một số thực không âm.
Phương pháp giải:
Lời giải:
.
Do đó C sai vì mô đun của số phức vẫn có thể bằng .
Cụ thể khi thì .
Chọn đáp án (C)
Các dạng toán về điểm biểu diễn số phức
1. Kiến thức cần nhớ
Điểm biểu diễn số phức .
2. Một số dạng toán thường gặp
Dạng 1: Tìm điểm biểu diễn số phức thỏa mãn điều kiện cho trước.
Phương pháp:
Cách 1: Tính số phức dựa vào các phép đổi thông thường.
Cách 2:
– Bước 1: Gọi số phức có điểm biểu diễn là .
– Bước 2: Thay và điều kiện đề bài tìm .
Ví dụ: Cho số phức thỏa mãn biết . Tìm tọa độ điểm biểu diễn số phức .
Giải:
Gọi biểu diễn số phức , ta có:
Vậy .
Dạng 2: Tìm tập hợp điểm biểu diễn số phức.
Phương pháp:
– Bước 1: Gọi số phức có điểm biểu diễn là .
– Bước 2: Thay vào điều kiện đã cho dẫn đến phương trình liên hệ giữa .
– Bước 3: Kết luận:
+) Phương trình đường thẳng:
+) Phương trình đường tròn:
+) Phương trình parabol: hoặc
+) Phương trình elip:
Ví dụ: Tìm tập hợp các điểm biểu diễn số phức thỏa mãn:.
A. Đường tròn tâm và bán kính .
B. Đường tròn tâm và bán kính .
C. Đường tròn tâm và bán kính .
D. Đường tròn tâm và bán kính .
Giải:
Giả sử ta có số phức .
Thay vào có:
.
Chọn đáp án A
Các dạng toán về tìm min, max liên quan đến số phức
1. Kiến thức cần nhớ
– Mô đun của số phức là
– Bất đẳng thức Cô-si: với
– Bất đẳng thức Bunhiacopxki:
– Bất đẳng thức chứa dấu giá trị tuyệt đối:
2. Một số dạng toán thường gặp
Dạng 1: Tìm số phức thỏa mãn điều kiện có mô đun nhỏ nhất, lớn nhất.
Phương pháp:
– Bước 1: Gọi số phức .
– Bước 2: Thay và biểu thức đã cho tìm mối quan hệ của .
– Bước 3: Đánh giá biểu thức có được để tìm max, min, từ đó suy ra .
Ví dụ: Cho thỏa mãn Tính max
A.
B.
C.
D.
Giải
Đặt . Điều kiện đã cho trở thành
+)
(1)
+)
(2)
Cộng vế với vế của (1) và (2) ta được
+)
Áp dụng bất đẳng thức Bunhiacopxki ta được
Đáp án D
Lưu ý: Có thể sử dụng phương pháp hình học để giải các bài tập dạng này.
Phương pháp:
Bước 1: Tìm tập hợp điểm biểu diễn của số phức. Có 4 tập hợp điểm thường gặp
+) Đường thẳng
+) Đường tròn
+) Đường elip
+) Parabol
Bước 2: Vẽ tập hợp điểm biểu diễn của số phức. Từ đó tìm max, min của mô đun
Số phức có điểm biểu diễn là . Mô đun của số phức là độ dài đoạn thẳng với là gốc tọa độ.
Ví dụ: Cho số phức thỏa mãn đồng thời có mô đun nhỏ nhất. Tính
A.
B.
C.
D.
Giải
Gọi là điểm biểu diễn của số phức
+)
Suy ra tập hợp điểm biểu diễn của là một đường thẳng
+)
minminmin
Đáp án A.
Dạng 2: Tìm GTLN, GTNN của mô đun số phức thỏa mãn điều kiện cho trước.
Phương pháp:
– Sử dụng các bất đẳng thức Cô si, Bunhiacopxki và bất đẳng thức tam giác.
Ví dụ: Cho thỏa mãn Tìm max
A.
B.
C.
D.
Giải
Dấu hiệu: Đề bài yêu cầu tính max của một mô đun ta sử dụng bất đẳng thức chứa dấu giá trị tuyệt đôi.
Ta có:
max
Đáp án A.