Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
A. LÝ THUYẾT ỨNG DỤNG CỦA TÍCH PHÂN
1. Diện tích hình phẳng
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x) liên tục trên đoạn [a ; b], trục hoành và hai đường thẳng x=a, x=b được xác định: \(S = \int_a^b | f(x)|dx\)
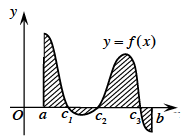
\((H)\left\{ {\begin{array}{*{20}{l}}{y = f(x)}\\{y = 0}\\{x = a}\\{x = b}\end{array}} \right.\)
\(S = \int_a^b | f(x)|dx\)
Diện tích hình phẳng giới hạn bới đồ thị hàm số y=f(x), y=g(x) liên tục trên đoạn [a ; b] và hai đường thẳng x=a, x=b được xác định: \(S = \int_a^b | f(x) – g(x)|dx\)
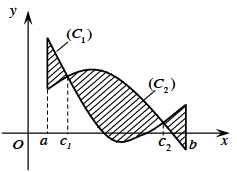
\((H)\left\{ {\begin{array}{*{20}{l}}{\left( {{C_1}} \right):y = {f_1}(x)}\\{\left( {{C_2}} \right):y = {f_2}(x)}\\{x = a}\\{x = b}\end{array}} \right.\)
\(S = \int_a^b {\left| {{f_1}(x) – {f_2}(x)} \right|} dx\)
Chú ý:
– Nếu trên đoạn [a ; b], hàm số f(x) không đổi dấu thì: \(\int_a^b | f(x)|dx = \left| {\int_a^b f (x)dx} \right|\)
– Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối
– Diện tích của hình phẳng giới hạn bởi các đường x=g(y), x=h(y) và hai đường thẳng y=c, y=d được xác định: \(S = \int_c^d | g(y) – h(y)|dy\)
2. Thể tích vật thể và thể tích khối tròn xoay
a) Thể tích vật thể:
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x \((a \le x \le b)\). Giả sử S(x) là hàm số liên tục trên đoạn [a ; b]

Khi đó, thể tích của vật thể B được xác định: \(V = \int_a^b S (x)dx\)
b) Thể tích khối tròn xoay:
Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y=f(x), trục hoành và hai đường thẳng x=a, x=b quanh trục Ox:
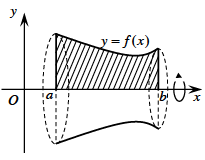
\(\left\{ {\begin{array}{*{20}{l}}{(C):y = f(x)}\\{(Ox):y = 0}\\{x = a}\\{x = b}\end{array}} \right.\)
\({V_x} = \pi \int\limits_a^b {{{\left[ {f(x)} \right]}^2}d{\rm{x}}} \)
Chú ý:
– Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x=g(y), trục hoành và hai đường thẳng y=c, y=d quanh trục Oy:
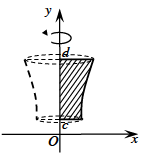
\(\left\{ {\begin{array}{*{20}{l}}{(C):y = g(y)}\\{(Oy):x = 0}\\{y = c}\\{y = d}\end{array}} \right.\)
\({V_y} = \pi \int\limits_c^d {{{\left[ {g(y)} \right]}^2}dy} \)
– Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y=f(x), y=g(x) và hai đường thẳng x=a, x=b quanh trục O x :
\(V = \pi \int_a^b {\left| {{f^2}(x) – {g^2}(x)} \right|} dx\)
B. CÂU HỎI TRẮC NGHIỆM
I. Câu hỏi tính diện tích hình phẳng giới hạn bởi các đường:
Những điểm cần lưu ý:
Trường hợp 1. Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a ; b]. Diện tích hình phẳng giới hạn bởi các đường y=f(x), y=g(x), x=a, x=b là \(S = \int_a^b | f(x) – g(x)|dx\).
Phương pháp giải toán
+) Giải phương trình f(x)=g(x) (1)
+) Nếu (1) vô nghiệm thì \(S = \left| {\int_a^b {(f(} x) – g(x))dx} \right|\).
+) Nếu (1) có nghiệm thuộc [a ; b]. giả sử \(\alpha \) thì
\(S = \left| {\int_a^\alpha {(f(} x) – g(x))dx} \right| + \left| {\int_a^b {(f(} x) – g(x))dx} \right|\)
Chú ý: Có thể lập bảng xét dấu hàm số f(x)-g(x) trên đoạn \([{\rm{a}};{\rm{b}}]\) rồi dựa vào báng xét dấu để tính tích phân.
Trường hợp 2. Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a ; b]. Diện tích hình phẳng giới hạn bởi các đường y=f(x), y=g(x) là \(S = \int_\alpha ^\beta {\left| {f(x) – g(x)} \right|} dx\). Trong đó \(\alpha ,\beta \) là nghiệm nhỏ nhất và lớn nhất của phương trình \(f(x) = g(x)(a \le \alpha < \beta \le b)\).
Phương pháp giải toán:
Buớc 1. Giải phương trình f(x)=g(x) tìm các giá trị \(\alpha ,\beta \).
Buớc 2. Tính \(S = \int_\alpha ^\beta {\left| {f(x) – g(x)} \right|} dx\) như trường hợp 1 .
BÀI TẬP
Câu 1. Công thức tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y=f(x), y=g(x) liên tục trên [a ; b] và hai đường thẳng \(x = a,x = b(a < b)\) là:
A. \(S = \pi \int_a^b {\left| {f(x) – g(x)} \right|} dx\).
B. \(S = \int_a^b {(f(} x) – g(x))dx\).
C. \(S = \int_a^b {(f(} x) – g(x){)^2}dx\).
D. \(S = \int_a^b {\left| {f(x) – g(x)} \right|} dx\).
Câu 2. Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y=f(x), liên tục trên [a ; b] trục hoành và hai đường thẳng \(x = a,x = b(a < b)\) cho bởi công thức:
A. \(S = \int_a^b {\left| {f(x)} \right|} dx.\)
B. \(S = \int_a^b f (x)dx\).
C. \(S = \pi \int_a^b {\left| {f(x)} \right|} dx\).
D. \(S = \pi \int_a^b {{f^2}} (x)dx\).
Câu 3. Diện tích hình phẳng giới hạn bởi các đường \(y = {x^3} + 11x – 6,y = 6{x^2},x = 0,x = 2\). (Đơn vị diện tích)
A. \(\frac{4}{3}\)
B. \(\frac{5}{2}\)
C. \(\frac{8}{3}\)
D. \(\frac{{18}}{{23}}\)
Câu 4. Diện tích hình phẳng giới hạn bởi \(y = {x^3},y = 4x\) là:
A. 8
B. 9
C. 12
D. 13
Câu 5. Cho hàm số y=f(x) liên tục và nhận giá trị không âm trên đoạn \(\left[ {a;b} \right]\). Diện tích hình thang cong giới hạn bởi đồ thị của y = f(x), trục hoành và hai đường thẳng x=a, x=b được tính theo công thức.
A. \(S = \int_a^b f (x)dx\)
B. \(S = – \int_a^b f (x)dx\).
C. \(S = – \int_a^b {{f^2}} (x)dx\).
D. \(S = \int_a^b {{f^2}} (x)dx\).
Câu 6. Diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y=f(x) liên tục trên đoạn [a ; b], trục hoành và hai đường thẳng x=a, x=b được tính theo công thức
A. \(S = \int_a^b {\left| {f(x)} \right|} dx.\)
B. \(S = \int_a^b f (x)dx\)
C. \(S = {\int_a^b {\left| {f(x)} \right|} ^2}dx\).
D. \(S = \pi \int_a^b f (x)dx\).
Câu 7. Diện tích hình phẳng được giới hạn bởi đồ thị các hàm số y=f(x), y=g(x) liên tục trên đoạn [a ; b], trục hoành và hai đường thẳng x=a, x=b được tính theo công thức
A. \(S = {\int_a^b {\left| {f(x) – g(x)} \right|} ^2}dx\)
B. \[S = \int\limits_a^b {\left[ {f(x) – g(x)} \right]} dx\].
C. \(S = \int_a^b {\left| {f(x) – g(x)} \right|} dx\).
D. \(S = \pi {\int_a^b {\left| {f(x) – g(x)} \right|} ^2}dx\).
Câu 8. Cho đồ thị hàm số y=f(x). Diện tích hình phẳng (phần tô đậm trong hình) là
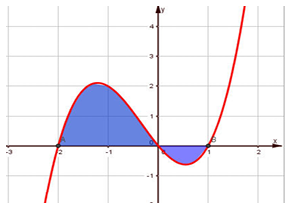
A. \(S = \int_{ – 2}^0 f (x)dx + \int_0^1 f (x)dx\)
B. \(S = \int_{ – 2}^1 f (x)dx\)
C. \(S = \int_0^{ – 2} f (x)dx + \int_0^1 f (x)dx\)
D. \(S = \int_{ – 2}^0 f (x)dx – \int_0^1 f (x)dx\)
Câu 9. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành và hai đường thẳng x=1, x=3 là
A. 19
B. 18
C. 20
D. 21
Câu 10. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = \sqrt x \), trục hoành và hai đường thẳng x=1, x=4 là
A. 4
B. \(\frac{{14}}{5}\)
C. \(\frac{{13}}{3}\)
D. \(\frac{{14}}{3}\)
Câu 11. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = \sqrt[3]{x}\), trục hoành và hai đường thẳng x=1, x=8 là
A. \(\frac{{45}}{2}\)
B. \(\frac{{45}}{4}\)
C. \(\frac{{45}}{7}\)
D. \(\frac{{45}}{8}\)
Câu 12. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y=sin x, trục hoành và hai đường thẳng \(x = \pi ,x = \frac{{3\pi }}{2}\) là
A. 1.
B. \(\frac{1}{2}\)
C. 2
D. \(\frac{3}{2}\)
Câu 13. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y=tan x, trục hoành và hai đường thẳng \(x = \frac{\pi }{6},x = \frac{\pi }{4}\) là
A. \(\ln \frac{{\sqrt 3 }}{3}\)
B. \(\ln \frac{{\sqrt 6 }}{3}\)
C. \( – \ln \frac{{\sqrt 3 }}{3}\)
D. \( – \ln \frac{{\sqrt 6 }}{3}\)
Câu 14. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {e^{2x}}\), trục hoành và hai đường thẳng x=0, x=3 là
A. \(\frac{{{e^6}}}{2} + \frac{1}{2}\)
B. \(\frac{{{e^6}}}{2} – \frac{1}{2}\)
C. \(\frac{{{e^6}}}{3} + \frac{1}{3}\)
D. \(\frac{{{e^6}}}{3} – \frac{1}{3}\)
II. Diện tích phẳng (vận dụng thấp)
Câu 15. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^3} – 3{x^2}\), trục hoành và hai đường thẳng x=1, x=4 là
A. \(\frac{{53}}{4}\)
B. \(\frac{{51}}{4}\)
C. \(\frac{{49}}{4}\)
D. \(\frac{{25}}{2}\)
Câu 16. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^4} – 3{x^2} – 4\), trục hoành và hai đường thẳng x=0, x=3 là
A. \(\frac{{142}}{5}\)
B. \(\frac{{143}}{5}\)
C. \(\frac{{144}}{5}\)
D. \(\frac{{141}}{5}\)
Câu 17. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = \frac{{x + 1}}{{x + 2}}\), trục hoành và đường thẳng x=2 là
A. 3+2 ln 2
B. 3-ln 2
C. 3-2 ln 2
D. 3+ln 2
Câu 18. Diện tích hình phẳng được giới hạn bởi parabol \(y = 2 – {x^2}\) và đường thẳng y=-x là
A. \(\frac{7}{2}\)
B. \(\frac{9}{4}\)
C. 3
D. \(\frac{9}{2}\)
Câu 19. Diện tích hình phẳng được giới hạn bới đồ thị hàm số y=cos 2 x, trục hoành và hai đường thẳng \(x = 0,x = \frac{\pi }{2}\) là
A. 2
B. 1
C. 3
D. 4
Câu 20. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^4} – 3{x^2} – 4\), trục hoành và hai đường thẳng x=0, x=3 là
A. \(\frac{{71}}{5}\)
B. \(\frac{{73}}{5}\)
C. \(\frac{{72}}{5}\)
D. 14
Câu 21. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = \frac{{x + 1}}{{x + 2}}\), trục hoành và đường thẳng x=2 là
A. 3+2 ln 2
B. 3-ln 2
C. 3-2 ln 2
D. 3+ln 2
Câu 22. Diện tích hình phẳng được giới hạn bởi parabol \(y = 2 – {x^2}\) và đường thẳng y=-x là
A. \(\frac{9}{2}\)
B. \(\frac{9}{4}\)
C. 3
D. \(\frac{7}{2}\)
Câu 23. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y=cos 2x, trục hoành và hai đường thẳng \(x = 0,x = \frac{\pi }{2}\) là
A. 1
B. 2
C. 3
D. 4
Xem thêm