Giải SGK Toán 7 Bài 13 (Cánh diều): Tính chất ba đường cao của tam giác

Giải bài tập Toán lớp 7 Bài 13: Tính chất ba đường cao của tam giác

A. Câu hỏi trong bài

Giải Toán 7 trang 116 Tập 2

Câu hỏi khởi động trang 116 Toán 7 Tập 2: Cho tam giác ABC. Gọi M, N, P lần lượt là hình chiếu của A, B, C trên các đường thẳng BC, CA, AB (Hình 132).

 

Em có nhận xét gì về ba đường thẳng AM, BN, CP.

Lời giải:

Vì M, N, P lần lượt là hình chiếu của A, B, C trên các đường thẳng BC, CA, AB nên AM, BN, CP lần lượt là ba đường cao tương ứng kẻ từ ba đỉnh A, B, C.

Quan sát Hình 132, ta thấy ba đường cao AM, BN, CP cùng đi qua một điểm.

Hoạt động 1 trang 116 Toán 7 Tập 2: Cho tam giác ABC (Hình 133).

 

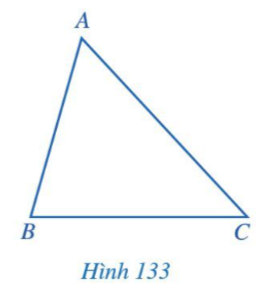
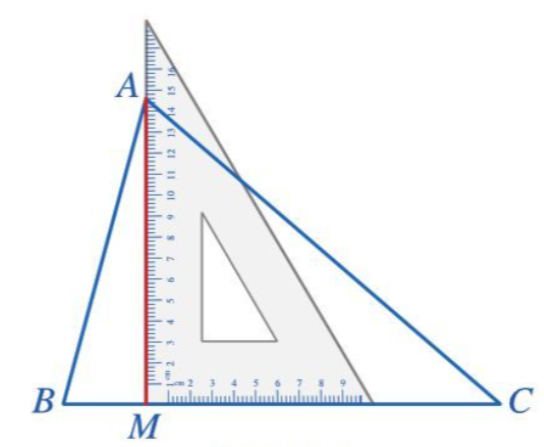
Bằng cách sử dụng ê ke, vẽ hình chiếu M của điểm A trên đường thẳng BC.

Lời giải:

Vì M là hình chiếu của điểm A trên đường thẳng BC nên AM $\perp$ BC tại M.

Do đó ta dùng hai cạnh góc vuông của thước ê ke để vẽ AM $\perp$ BC tại M bằng cách đặt thước như sau:

+ Một cạnh góc vuông của ê ke trùng với cạnh BC;

+ Một cạnh góc vuông còn lại của ê ke đi qua điểm A.

Khi đó ta vẽ đường thẳng theo cạnh góc vuông đó của ê ke, đường thẳng này cắt cạnh BC tại một điểm, điểm này là điểm M cần vẽ.

Ta có hình vẽ sau:

 

Giải Toán 7 trang 117 Tập 2

Luyện tập 1 trang 117 Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Hãy đọc tên đường cao đi qua B, đường cao đi qua C.

Lời giải:

 

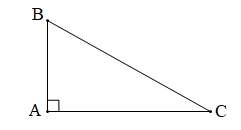
Tam giác ABC vuông tại A nên BA $\perp$ CA tại A.

Do đó:

+ Đường cao đi qua B và vuông góc với AC là AB.

+ Đường cao đi qua C và vuông góc với AB là AC.

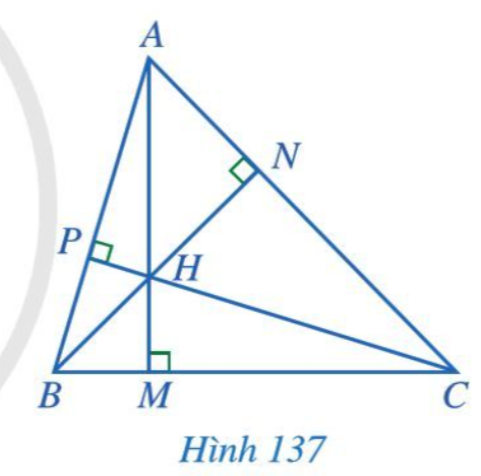
Hoạt động 2 trang 117 Toán 7 Tập 2: Quan sát ba đường cao AM, BN, CP của tam giác ABC (Hình 137), cho biết ba đường cao đó có cùng đi qua một điểm hay không.

 

Lời giải:

Quan sát Hình 132, ta thấy ba đường cao AM, BN, CP cùng đi qua điểm H.

Luyện tập 2 trang 117 Toán 7 Tập 2: Cho tam giác đều ABC có trọng tâm là G. Chứng minh G cũng là trực tâm của tam giác ABC.

Lời giải:

GT	$∆$ABC đều, G là trọng tâm của $∆$ABC
KL	G là trực tâm của $∆$ABC

Chứng minh (Hình vẽ dưới đây):

 

Gọi M, N theo thứ tự là trung điểm của AB và AC.

Vì tam giác ABC đều (giả thiết) nên AB = BC = CA.

Mà M là trung điểm của AB nên AM = BM.

Xét $∆$AMC và $∆$BMC có:

AC = BC (chứng minh trên),

MC là cạnh chung,

AM = BM (chứng minh trên).

Do đó $∆$AMC = $∆$BMC  (c.c.c).

Suy ra $\widehat{AMC}=\widehat{BMC}$ (hai góc tương ứng).

Mà $\widehat{AMC}+\widehat{BMC}=180°$ nên $\widehat{AMC}=\widehat{BMC}=\frac{180°}{2}=90°$.

Do đó CM $\perp$ AB tại M.

Do đó CM là đường cao kẻ từ đỉnh C của tam giác ABC.

Chứng minh tương tự ta cũng có BN là đường cao kẻ từ đỉnh B của tam giác ABC.

Tam giác ABC có hai đường cao BN và CM cắt nhau tại G nên G là trực tâm của tam giác ABC.

Vậy G là trực tâm của tam giác ABC.

Giải Toán 7 trang 118 Tập 2

Luyện tập 3 trang 118 Toán 7 Tập 2: Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều.

Lời giải:

GT	$∆$ABC, H là trực tâm của $∆$ABC, H là trọng tâm của $∆$ABC
KL	$∆$ABC đều.

Chứng minh (Hình vẽ dưới đây):

 

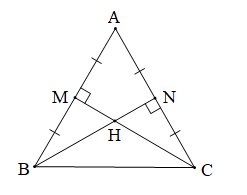
Gọi M, N lần lượt là trung điểm của AB và AC.

Do H là trực tâm đồng thời là trọng tâm của tam giác ABC (giả thiết) nên:

+) CM $\perp$ AB tại trung điểm M của AB, do đó CM là đường trung trực của AB

Nên C nằm trên đường trung trực của AB suy ra CA = CB. (1)

+) BN $\perp$ AC tại trung điểm N của AC, do đó BN là đường trung trực của AC

Nên B nằm trên đường trung trực của AC suy ra BA = BC. (2)

Từ (1) và (2) suy ra AB = BC = CA nên tam giác ABC đều.

Vậy tam giác ABC đều.

B. Bài tập

Bài 1 trang 118 Toán 7 Tập 2: Cho tam giác ABC có H là trực tâm, H không trùng với đỉnh nào của tam giác. Nêu một tính chất của cặp đường thẳng:

a) AH và BC;

b) BH và CA;

c) CH và AB.

Lời giải:

 

a) Vì H là trực tâm của tam giác ABC nên AH $\perp$ BC.

b) Vì H là trực tâm của tam giác ABC nên BH $\perp$ CA.

c) Vì H là trực tâm của tam giác ABC nên CH $\perp$ AB.

Bài 2 trang 118 Toán 7 Tập 2: Cho tam giác ABC. Vẽ trực tâm H của tam giác ABC và nhận xét vị trí của nó trong các trường hợp sau:

a) Tam giác ABC nhọn;

b) Tam giác ABC vuông tại A;

c) Tam giác ABC có góc A tù.

Lời giải:

a) Ta có hình vẽ sau:

 

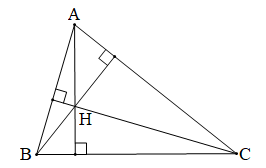
Trong hình vẽ trên, điểm H nằm trong tam giác ABC.

b) Ta có hình vẽ sau:

 

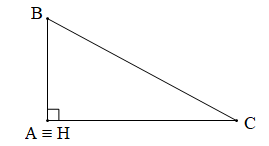
Tam giác ABC vuông tại A nên BA $\perp$ CA tại A.

Do đó BA và CA là hai đường cao kẻ từ đỉnh B và đỉnh C của tam giác ABC.

Mà BA cắt CA tại A nên A là trực tâm của tam giác ABC.

Do đó điểm H trùng với điểm A.

c) Ta có hình vẽ sau:

 

Trong hình vẽ trên, điểm H nằm ngoài tam giác ABC.

Bài 3 trang 118 Toán 7 Tập 2: Cho tam giác nhọn ABC và điểm D nằm trong tam giác. Chứng minh rằng nếu DA vuông góc với BC và DB vuông góc với CA thì DC vuông góc với AB.

Lời giải:

GT	$∆$ABC nhọn, D nằm trong tam giác, DA $\perp$ BC, DB $\perp$ CA.
KL	DC $\perp$AB.

Chứng minh (Hình vẽ dưới đây):

 

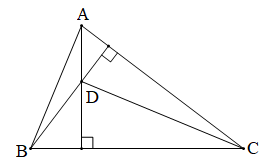
Tam giác ABC có DA $\perp$ BC, DB $\perp$ CA (giả thiết)

Mà DA cắt DB tại D nên D là trực tâm của tam giác ABC.

Do đó DC $\perp$ AB.

Vậy DC $\perp$ AB.

Bài 4 trang 118 Toán 7 Tập 2: Cho tam giác nhọn ABC. Hai đường cao BE và CF cắt nhau tại H, $\widehat{HCA}=25°$. Tính $\widehat{BAC}$ và $\widehat{HBA}$.

Lời giải:

GT	DABC nhọn, BE $\perp$ AC, CF $\perp$AB, BE và CF cắt nhau tại H, $\widehat{HCA}=25°$
KL	Tính $\widehat{BAC}$ và $\widehat{HBA}$.

Chứng minh (Hình vẽ dưới đây):

 

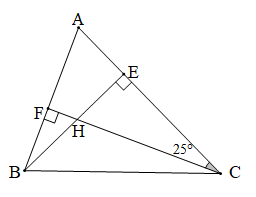
Vì CF $\perp$ AB (giả thiết) nên tam giác ACF vuông tại F.

Xét $∆$ACF vuông tại F: $\widehat{FCA}+\widehat{F\text{A}C}=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau).

Suy ra $\widehat{F\text{A}C}=90°-\widehat{FCA}=90°-25°=65°$ hay $\widehat{BAC}=65°$.

Vì BE $\perp$ AC (giả thiết) nên tam giác ABE vuông tại E.

Xét $∆$ABE vuông tại E: $\widehat{ABE}+\widehat{\text{BAE}}=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau).

Suy ra $\widehat{ABE}=90°-\widehat{BAE}=90°-65°=25°$ hay $\widehat{HBA}=25°$.

Vậy $\widehat{BAC}=65°$ và $\widehat{HBA}=25°$.

Bài 5 trang 118 Toán 7 Tập 2: Trong Hình 139, cho biết AB // CD, AD // BC; H, K lần lượt là trực tâm các tam giác ABC và ACD. Chứng minh AK // CH và AH // CK.

 

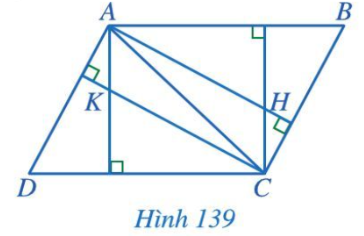
Lời giải:

GT	AB // CD, AD // BC; H là trực tâm tam giác ABC, K là trực tâm tam giác ACD.
KL	AK // CH và AH // CK.

Chứng minh (Hình 139):

+) Vì K là trực tâm của tam giác ACD (giả thiết) nên AK $\perp$ CD.

Mà AB // CD (giả thiết) nên AK $\perp$ AB.

Vì H là trực tâm của tam giác ABC (giả thiết) nên CH $\perp$ AB.

Do đó AK // CH.

+) Vì K là trực tâm của tam giác ACD (giả thiết) nên CK $\perp$ AD.

Mà AD // BC (giả thiết) nên CK $\perp$ BC.

Vì H là trực tâm của tam giác ABC (giả thiết) nên AH $\perp$ BC.

Do đó AH // CK.

Bài 6 trang 118 Toán 7 Tập 2: Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Chứng minh rằng:

a) Nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau;

b) Nếu tam giác ABC có hai điểm H, I trùng nhau thì tam giác ABC là tam giác đều.

Lời giải:

a)

GT	$∆$ABC đều, G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực.
KL	Bốn điểm G, H, I, O trùng nhau.

Chứng minh (Hình vẽ dưới đây):

 

Kéo dài AI cắt BC tại M, kéo dài BI cắt AC tại N, kéo dài CP cắt AB tại P.

Khi đó AM là đường phân giác của $\widehat{BAC}$ nên $\widehat{BAM}=\widehat{CAM};$

Do tam giác ABC đều nên AB = BC = CA.

Xét $∆$ABM và $∆$ACM có:

AB = AC (chứng minh trên),

$\widehat{BAM}=\widehat{CAM}$ (chứng minh trên),

AM là cạnh chung

Do đó $∆$ABM = $∆$ACM  (c.g.c).

Suy ra:

• $\widehat{AMB}=\widehat{AMC}$ (hai góc tương ứng);

• BM = CM (hai cạnh tương ứng).

Vì BM = CM nên M là trung điểm của BC.

Ta có $\widehat{AMB}=\widehat{AMC}$, mà $\widehat{AMB}+\widehat{AMC}=180°$ nên $\widehat{AMB}=\widehat{AMC}=\frac{180°}{2}=90°$.

Khi đó AM $\perp$ BC tại trung điểm M của BC nên AM là đường trung trực của đoạn thẳng BC cũng đồng thời là đường cao và đường trung tuyến kẻ từ A của $∆$ABC.

Chứng minh tương tự ta cũng có:

+) BN là đường trung trực của đoạn thẳng AC, đồng thời là đường cao và đường trung tuyến kẻ từ B của $∆$ABC.

+) CP là đường trung trực của đoạn thẳng AB, đồng thời là đường cao và đường trung tuyến kẻ từ C của $∆$ABC.

Mà AM, BN, CP cắt nhau tại I nên G, H, I, O trùng nhau.

b)

GT	$∆$ABC, H là trực tâm, I là giao điểm của ba đường phân giác, I ≡ H
KL	$∆$ABC đều

Chứng minh (Hình vẽ dưới đây):

 

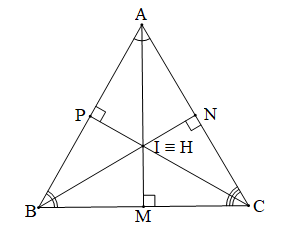
Vì I là giao điểm ba đường phân giác, H là trực tâm của tam giác ABC (giả thiết) nên:

+ AI là đường phân giác và AH là đường cao kẻ từ A của $∆$ABC.

Mà I ≡ H (giả thiết) nên đường phân giác AI trùng với đường cao AH.

+ Tương tự đường phân giác BI trùng đường cao BH;

+ Đường phân giác CI trùng đường cao CH.

Gọi M, N, P lần lượt là chân đường cao (hay cũng chính là đường phân giác) kẻ từ A, B, C đến BC, CA, AB.

Xét $∆$ABM (vuông tại M) và $∆$ACM (vuông tại M) có:

$\widehat{BAM}=\widehat{CAM}$ (do AM là tia phân giác của $\widehat{BAC}$),

AM là cạnh chung

Do đó $∆$ABM = $∆$ACM (cạnh góc vuông – góc nhọn kề).

Suy ra AB = AC (hai cạnh tương ứng). (1)

Xét $∆$ABN (vuông tại N) và $∆$CBN (vuông tại N) có:

BN là cạnh chung,

$\widehat{ABN}=\widehat{CBN}$ (do BN là tia phân giác của $\widehat{ABC}$),

Do đó $∆$ABN = $∆$CBN (cạnh góc vuông – góc nhọn kề).

Suy ra AB = BC (hai cạnh tương ứng). (2)

Từ (1) và (2) suy ra AB = BC = CA do đó tam giác ABC là tam giác đều.

Vậy tam giác ABC đều.

Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:

Giải SGK Toán 7 Bài 10: Tính chất ba đường trung tuyến của tam giác

Giải SGK Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác

Giải SGK Toán 7 Bài 12: Tính chất ba đường trung trực của tam giác

Giải SGK Toán 7 Bài 13: Tính chất ba đường cao của tam giác

Giải SGK Toán 7: Bài tập cuối chương 7