Lý thuyết Toán 7 Chương 3 (Kết nối tri thức 2023): Góc và đường thẳng song song hay, chi tiết

Lý thuyết Toán lớp 7 Chương 3: Góc và đường thẳng song song

A. Lý thuyết Chương 3: Góc và đường thẳng song song

1. Góc ở vị trí đặc biệt

a) Hai góc kề bù

• Định nghĩa: Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.

• Tính chất: Hai góc kề bù có tổng số đo bằng 180°.

+ Góc $\widehat{\mathrm{xOy}}$ và $\widehat{\mathrm{yOz}}$ có cạnh Oy chung; Ox và Oz là hai tia đối nhau. Do đó $\widehat{\mathrm{xOy}}$ và $\widehat{\mathrm{yOz}}$ được gọi là hai góc kề bù.

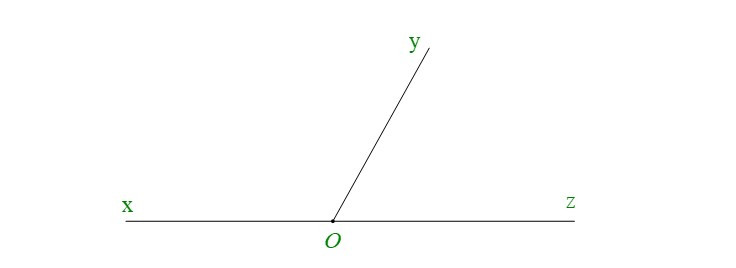
+ Vì $\widehat{\mathrm{xOy}}$ và $\widehat{\mathrm{yOz}}$ là hai góc kề bù nên $\widehat{\mathrm{xOy}}+\widehat{\mathrm{yOz}}=180°$.

• Hai góc kề bù được hiểu là hai góc vừa kề nhau, vừa bù nhau. Trong đó:

Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm khác phía nhau đối với đường thẳng chứa cạnh chung đó.

• Nếu điểm M nằm trong góc xOy thì ta nói tia OM nằm giữa hai cạnh (hai tia) Ox và Oy của góc xOy. Khi đó ta có: $\widehat{\mathrm{xOM}}+\widehat{\mathrm{MOy}}=\widehat{\mathrm{xOy}}$

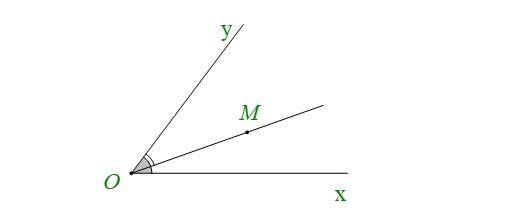
b) Hai góc đối đỉnh

• Định nghĩa: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

• Tính chất: Hai góc đối đỉnh thì bằng nhau.

Ví dụ:

+ Hai đường thẳng $\mathrm{xx}‘$, $\mathrm{yy}‘$ cắt nhau tại O. Khi đó $\text{Ox}$ và $\text{Ox}‘$ là hai tia đối nhau; $\text{Oy}$ và $\text{Oy}‘$ là hai tia đối nhau. Nên ta có các cặp góc đối đỉnh là: $\widehat{\mathrm{xOy}}$ và $\widehat{\mathrm{x}‘\mathrm{Oy}‘}$; $\widehat{\mathrm{xOy}‘}$ và $\widehat{\mathrm{x}‘\mathrm{Oy}}$.

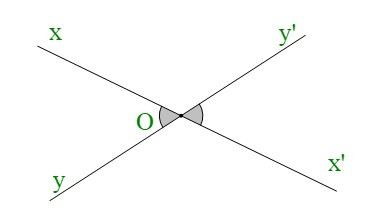
+ Có $\widehat{\mathrm{xOy}}$ và $\widehat{\mathrm{x}‘\mathrm{Oy}‘}$ là hai góc đối thì $\widehat{\mathrm{xOy}}=\widehat{\mathrm{x}‘\mathrm{Oy}‘}$.

• Hai đường thẳng $\mathrm{xx}‘$, $\mathrm{yy}‘$ cắt nhau và trong các góc tạo thành có một góc vuông được gọi là hai đường thẳng vuông góc. Kí hiệu là: $\mathrm{xx}‘\perp \mathrm{yy}‘$.

Ví dụ: Hai đường thẳng $\mathrm{xx}‘$, $\mathrm{yy}‘$ cắt nhau tại O sao cho $\widehat{\mathrm{xOy}}=90°$ thì $\mathrm{xx}‘\perp \mathrm{yy}‘$.

2. Tia phân giác của một góc

• Định nghĩa: Tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.

• Tính chất: Khi Oz là tia phân giác của góc xOy thì $\widehat{\mathrm{xOz}}=\widehat{\mathrm{yOz}}=\frac{1}{2}\widehat{\mathrm{xOy}}$.

• Đường thẳng chứa tia phân giác của một góc gọi là đường phân giác của góc đó.

Ví dụ:

+ Cho $\widehat{\mathrm{xOy}}=80°$ và Oz là tia phân giác của góc xOy. Khi đó ta có:

$\widehat{\mathrm{xOz}}=\widehat{\mathrm{yOz}}=\frac{1}{2}\widehat{\mathrm{xOy}}=\frac{1}{2}80°=40°$

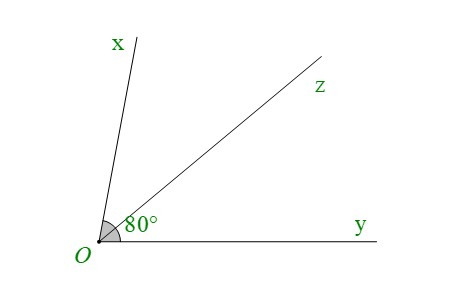
3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng

• Cho đường thẳng c cắt hai đường thẳng a và b lần lượt tại A và B tạo thành bốn góc đỉnh A và bốn góc đỉnh B. Khi đó ta có:

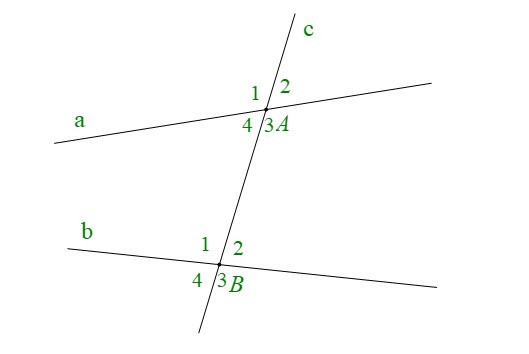
  + Các cặp góc so le trong là: A₃ và B₁; A₄ và B₂.

  + Các cặp góc đồng vị là: A₁ và B₁; A₂ và B₂; A₃ và B₃; A₄ và B₄.

  + Các cặp góc trong cùng phía là: A₄ và B₁; A₃ và B₂.

• Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:

  + Hai góc so le trong còn lại bằng nhau.

  + Hai góc đồng vị bằng nhau.

Ví dụ:

+ Cho đường thẳng c cắt hai đường thẳng phân biệt a, b lần lượt tại A và B.

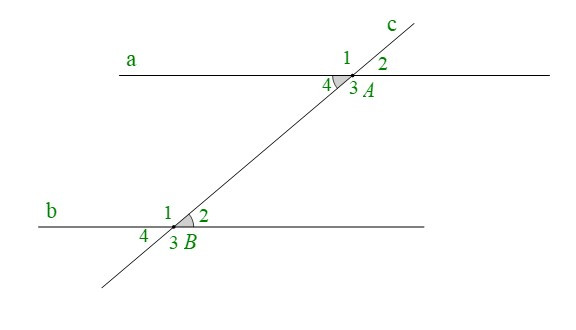
Nói rõ $\widehat{{\mathrm{A}}_4};\widehat{{\mathrm{B}}_2}$ là cặp góc so le trong

Nếu $\widehat{{\mathrm{A}}_4}=\widehat{{\mathrm{B}}_2}$ thì $\left\{\begin{array}{l}\widehat{{\mathrm{A}}_3}=\widehat{{\mathrm{B}}_1}\\ \widehat{{\mathrm{A}}_1}=\widehat{{\mathrm{B}}_1};\widehat{{\mathrm{A}}_2}=\widehat{{\mathrm{B}}_2};\widehat{{\mathrm{A}}_3}=\widehat{{\mathrm{B}}_3};\widehat{{\mathrm{A}}_4}=\widehat{{\mathrm{B}}_4}\end{array}\right.$ (cặp góc so le trong còn lại và các cặp góc đồng vị).

4. Dấu hiệu nhận biết hai đường thẳng song song

• Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a và b song song với nhau. Kí hiệu là: $\mathrm{a}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{b}$.

• Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.

5. Tiên đề Euclid về đường thẳng song song

• Tiên đề Euclid: Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.

• Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng cắt đường thẳng còn lại.

6. Tính chất của hai đường thẳng song song

• Nếu một đường thẳng cắt hai đường thẳng song song thì:

+ Hai góc so le trong bằng nhau;

+ Hai góc đồng vị bằng nhau.

Ví dụ: Cho $\mathrm{xy}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{x}‘\mathrm{y}‘$ và $\widehat{\mathrm{BAy}}=50°$. Tính $\widehat{\mathrm{ABx}‘}$ và $\widehat{\mathrm{y}‘\mathrm{Bz}‘}$

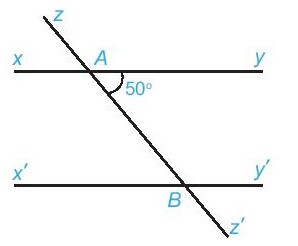
Vì $\mathrm{xy}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{x}‘\mathrm{y}‘$$\Rightarrow$$\widehat{\mathrm{ABx}‘}=\widehat{\mathrm{BAy}}$ (hai góc so le trong). Do đó $\widehat{\mathrm{ABx}‘}=50°$

Vì $\mathrm{xy}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{x}‘\mathrm{y}‘$$\Rightarrow$$\widehat{\mathrm{y}‘\mathrm{Bz}‘}=\widehat{\mathrm{BAy}}$ (hai góc đồng vị). Do đó $\widehat{\mathrm{y}‘\mathrm{Bz}‘}=50°$

• Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.

Ví dụ: Cho $\mathrm{xy}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{x}‘\mathrm{y}‘$ và $\mathrm{zz}‘\perp \mathrm{xx}‘$ thì $\mathrm{zz}‘\perp \mathrm{yy}‘$

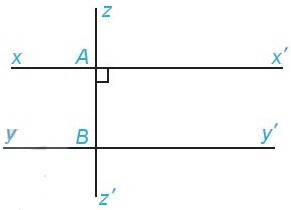
• Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.

Ví dụ: Cho $\mathrm{a}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{b}$ và $\mathrm{c}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{b}$ thì $\mathrm{a}\text{\hspace{0.17em}//\hspace{0.17em}c}$

7. Định lí. Giả thiết và kết luận của định lí

• Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng:

Nếu … thì …

+ Phần giữa từ “nếu” và từ “thì” là giả thiết của định lí.

+ Phần sau từ “thì” là kết luận của định lí.

Giả tiết, kết luận viết tắt tương ứng là GT và KL.

• Chứng minh một định lí là dùng lập luận để từ giả thiết và những khẳng định đúng đã biết suy ra kết luận của định lí.

B. Bài tập tự luyện

B1. Bài tập tự luận

Bài 1. Cho hình vẽ dưới đây. Biết Ax song song với Cy.

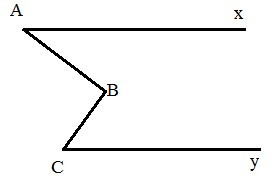
Chứng minh rằng $\widehat{\mathrm{xAB}}+\widehat{\mathrm{BCy}}=\widehat{\mathrm{ABC}}$

Hướng dẫn giải

GT	$\text{Ax\hspace{0.17em}//\hspace{0.17em}}\mathrm{Cy}$
KL	$\widehat{\mathrm{xAB}}+\widehat{\mathrm{BCy}}=\widehat{\mathrm{ABC}}$

Qua B, kẻ đường thẳng mn song song với đường thẳng chứa tia Ax.

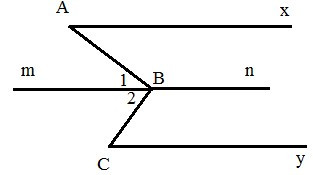
Vì $\text{Ax\hspace{0.17em}//\hspace{0.17em}}\mathrm{mn}$ nên $\widehat{\mathrm{xAB}}=\widehat{{\mathrm{B}}_1}$ (hai góc so le trong)  (1)

Vì $\text{Ax\hspace{0.17em}//\hspace{0.17em}}\mathrm{mn}$ mà $\text{Ax\hspace{0.17em}//}\mathrm{Cy}$ (giả thiết)

Do đó: $\text{mn\hspace{0.17em}//\hspace{0.17em}}\mathrm{Cy}$ (tính chất hai đường thẳng song song)

Vì $\text{mn\hspace{0.17em}//\hspace{0.17em}}\mathrm{Cy}$ nên $\widehat{\mathrm{BCy}}=\widehat{{\mathrm{B}}_2}$ (hai góc so le trong) (2)

Từ (1) và (2) ta có: $\widehat{\mathrm{xAB}}+\widehat{\mathrm{BCy}}=\widehat{{\mathrm{B}}_1}+\widehat{{\mathrm{B}}_2}$

Mà $\widehat{\mathrm{ABC}}=\widehat{{\mathrm{B}}_1}+\widehat{{\mathrm{B}}_2}$

Vậy $\widehat{\mathrm{xAB}}+\widehat{\mathrm{BCy}}=\widehat{\mathrm{ABC}}$ (đpcm)

Bài 2. Cho hình vẽ, biết $\mathrm{mn}\text{//}\mathrm{ab}$ và $\widehat{\mathrm{xHm}}=120°$.

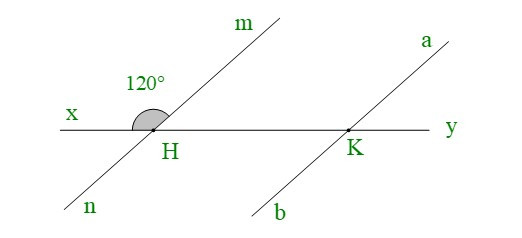
Tính các góc còn lại trong hình vẽ.

Hướng dẫn giải

Ta có: $\widehat{\mathrm{nHy}}=\widehat{\mathrm{xHm}}$ (hai góc đối đỉnh)

$\Rightarrow$$\widehat{\mathrm{nHy}}=120°$

Ta có: $\widehat{\mathrm{xHm}}+\widehat{\mathrm{xHn}}=180°$ (hai góc kề bù)

Thay số: $120°+\widehat{\mathrm{xHn}}=180°$

$\to$$\widehat{\mathrm{xHn}}=180°-120°$

$\widehat{\mathrm{xHn}}=60°$

Có: $\widehat{\mathrm{mHy}}=\widehat{\mathrm{xHn}}$ (hai góc đối đỉnh)

$\Rightarrow$$\widehat{\mathrm{mHy}}=60°$

Vì $\mathrm{mn}\text{//}\mathrm{ab}$ nên:

$\widehat{\mathrm{xKb}}=\widehat{\mathrm{mHy}}$ (hai góc so le trong) $\Rightarrow$$\widehat{\mathrm{xKb}}=60°$

$\widehat{\mathrm{xKa}}=\widehat{\mathrm{xHm}}$ (hai góc đồng vị) $\Rightarrow$$\widehat{\mathrm{xKa}}=120°$

$\widehat{\mathrm{aKy}}=\widehat{\mathrm{mHy}}$ (hai góc đồng vị) $\Rightarrow$$\widehat{\mathrm{aKy}}=60°$

$\widehat{\mathrm{bKy}}=\widehat{\mathrm{nHy}}$ (hai góc đồng vị) $\Rightarrow$$\widehat{\mathrm{bKy}}=120°$

Vậy $\widehat{\mathrm{nHy}}=120°$; $\widehat{\mathrm{xHn}}=60°$; $\widehat{\mathrm{mHy}}=60°$; $\widehat{\mathrm{xKb}}=60°$; $\widehat{\mathrm{xKa}}=120°$; $\widehat{\mathrm{aKy}}=60°$; $\widehat{\mathrm{bKy}}=120°$.

Bài 3. Cho hình vẽ dưới đây, biết $\widehat{\mathrm{mAt}}=125°$. Tính số đo các góc còn lại trong hình vẽ.

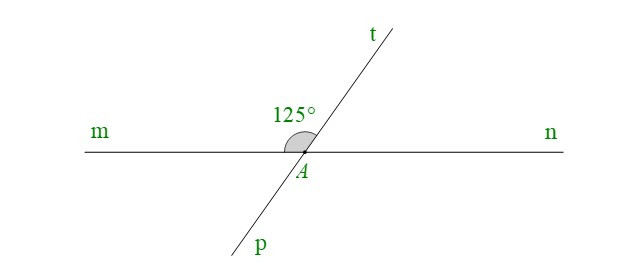
Hướng dẫn giải

Ta có: $\widehat{\mathrm{nAp}}=\widehat{\mathrm{mAt}}$ (hai góc đối đỉnh)

$\Rightarrow$$\widehat{\mathrm{nAp}}=125°$

Ta có:     $\widehat{\mathrm{mAt}}+\widehat{\mathrm{nAt}}=180°$ (hai góc kề bù)

Thay số: $125°+\widehat{\mathrm{nAt}}=180°$

$\Rightarrow$$\widehat{\mathrm{nAt}}=180°-125°$

$\widehat{\mathrm{nAt}}=55°$

Lại có: $\widehat{\mathrm{mAp}}=\widehat{\mathrm{nAt}}$ (hai góc đối đỉnh)

$\Rightarrow$$\widehat{\mathrm{mAp}}=55°$

Vậy: $\widehat{\mathrm{nAp}}=125°$; $\widehat{\mathrm{nAt}}=55°$; $\widehat{\mathrm{mAp}}=55°$.

Bài 4. Vẽ góc xOy có số đo bằng 72°. Vẽ tia Om là tia đối của tia Ox.

a) Viết tên cặp góc kề bù trong hình vừa vẽ.

b) Tính số đo góc yOm.

c) Vẽ tia Ot là tia phân giác của góc xOy. Tính số đo các góc tOy và tOm.

Hướng dẫn giải

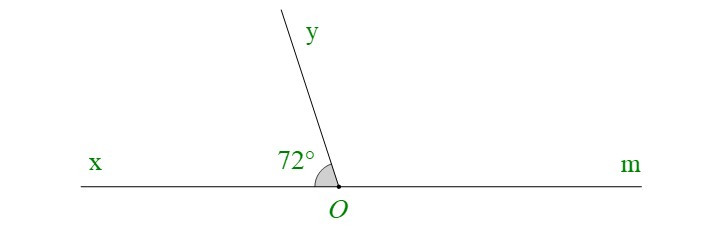
a) $\widehat{\mathrm{xOy}}$ và $\widehat{\mathrm{yOm}}$ có Oy chung; Om là tia đối của tia Ox.

$\Rightarrow$$\widehat{\mathrm{xOy}}$ và $\widehat{\mathrm{yOm}}$ là hai góc kề bù.

b) Ta có: $\widehat{\mathrm{xOy}}+\widehat{\mathrm{yOm}}=180°$ (hai góc kề bù)

Thay số: $72°+\widehat{\mathrm{yOm}}=180°$

$\Rightarrow$$\widehat{\mathrm{yOm}}=180°-72°$

$\widehat{\mathrm{yOm}}=108°$

Vậy: $\widehat{\mathrm{yOm}}=108°$

c)

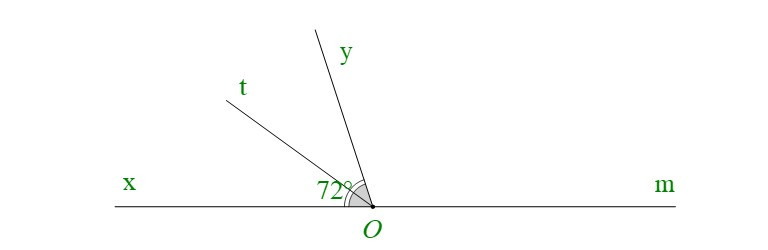
Vì Ot là tia phân giác của góc xOy nên: $\widehat{\mathrm{tOy}}=\widehat{\text{tOx}}=\frac{1}{2}\widehat{\mathrm{xOy}}=\frac{1}{2}\cdot 72°=36°$

Có: $\widehat{\mathrm{tOm}}+\widehat{\text{tOx}}=180°$ (hai góc kề bù)

Thay số: $\widehat{\mathrm{tOm}}+36°=180°$

$\Rightarrow$$\widehat{\mathrm{tOm}}=180°-36°$

$\widehat{\mathrm{tOm}}=144°$

Vậy: $\widehat{\text{tOy}}=36°$; $\widehat{\mathrm{tOm}}=144°$.

Bài 5. Cho hình vẽ dưới đây, hãy kể tên các cặp góc kề bù.

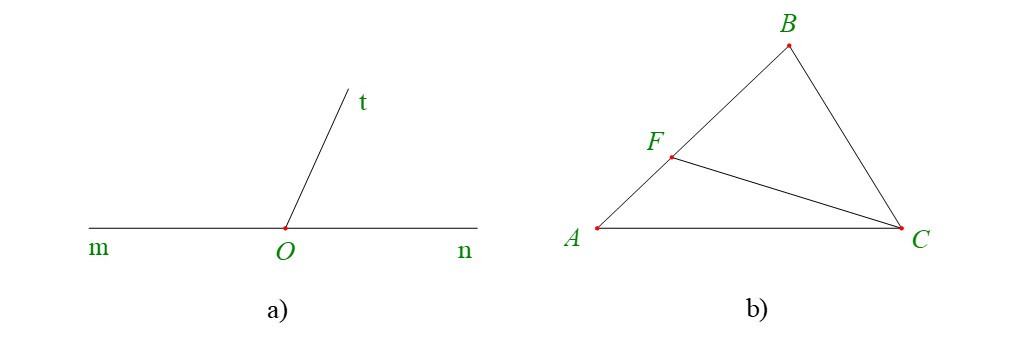
Hướng dẫn giải

a) Hai góc $\widehat{\mathrm{mOt}}$ và $\widehat{\mathrm{nOt}}$ có cạnh Ot chung; cạnh Om và On là hai tia đối nhau.

 Nên $\widehat{\mathrm{mOt}}$ và $\widehat{\mathrm{nOt}}$ là cặp góc kề bù.

b) Hai góc $\widehat{\mathrm{CFA}}$ và $\widehat{\mathrm{CFB}}$ có cạnh FC chung; cạnh FA và FB là hai tia đối nhau.

 Nên $\widehat{\mathrm{CFA}}$ và $\widehat{\mathrm{CFB}}$ là cặp góc kề bù.

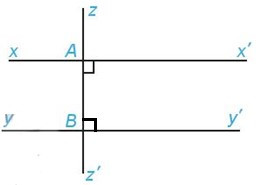
Bài 6. Vẽ hình, viết giả thiết, kết luận và chứng minh định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.

Hướng dẫn giải

GT	$\mathrm{xx}‘$ và $\mathrm{yy}‘$ là hai đường thẳng phân biệt $\mathrm{xx}‘\perp \mathrm{zz}‘$ tại A $\mathrm{yy}‘\perp \mathrm{zz}‘$ tại B
KL	$\mathrm{xx}‘\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{yy}‘$

Vì $\mathrm{xx}‘\perp \mathrm{zz}‘$ tại A  nên $\widehat{\mathrm{x}‘\mathrm{AB}}=90°$

Vì $\mathrm{yy}‘\perp \mathrm{zz}‘$ tại B  nên $\widehat{\mathrm{z}‘\mathrm{By}‘}=90°$

Nên $\widehat{\mathrm{x}‘\mathrm{AB}}=\widehat{\mathrm{z}‘\mathrm{By}‘}=90°$

Mà hai góc ở vị trí đồng vị.

Do đó $\mathrm{xx}‘\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{yy}‘$ (dấu hiệu nhận biết hai đường thẳng song song).

Bài 7. Cho hình dưới đây. Giải thích tại sao:

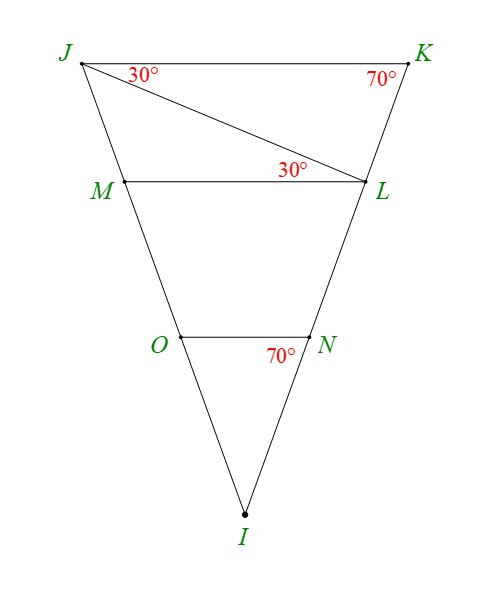
a) $\mathrm{JK}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{ML}$;

b) $\mathrm{JK}\text{\hspace{0.17em}//\hspace{0.17em}ON}$;

c) $\mathrm{MN}\text{\hspace{0.17em}//\hspace{0.17em}ON}$.

Hướng dẫn giải

a) Ta có: $\widehat{\mathrm{KJL}}=\widehat{\mathrm{JLM}}=30°$

Mà hai góc ở vị trí so le trong.

Do đó $\mathrm{JK}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{ML}$ (dấu hiệu nhận biết hai đường thẳng song song).

b) Ta có: $\widehat{\mathrm{JKL}}=\widehat{\mathrm{ONI}}=70°$

Mà hai góc ở vị trí đồng vị.

Do đó $\mathrm{JK}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{ON}$ (dấu hiệu nhận biết hai đường thẳng song song).

c) Ta có: $\mathrm{JK}\text{\hspace{0.17em}//\hspace{0.17em}ML}$ (theo câu a) và $\mathrm{JK}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{ON}$ (theo câu b)

Do đó $\mathrm{MN}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{ON}$ (tính chất hai đường thẳng song song).

Bài 8. Cho tam giác ABC. Vẽ đường thẳng m đi qua A và song song với BC. Vẽ đường thẳng n đi qua B và song song với AC. Có thể vẽ được bao nhiêu đường thẳng m, bao nhiêu đường thẳng n? Vì sao?

Hướng dẫn giải

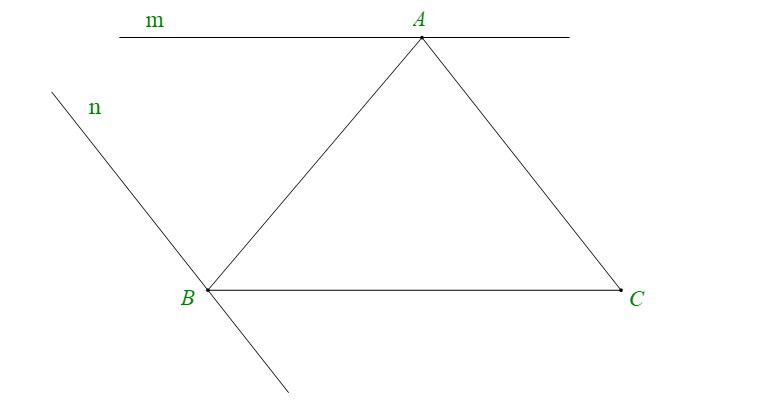
Vì theo tiên đề Euclid, qua điểm A ở ngoài BC, chỉ có một đường thẳng song song với BC. Nên chỉ vẽ được một đường thẳng m duy nhất.

Vì theo tiên đề Euclid, qua điểm B ở ngoài AC, chỉ có một đường thẳng song song với AC. Nên chỉ vẽ được một đường thẳng n duy nhất.

Bài 9. Vẽ hình, viết giả thiết, kết luận và chứng minh định lí: “Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông”.

Hướng dẫn giải

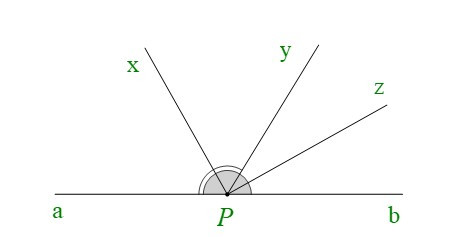
GT	$\widehat{\mathrm{aPy}}$ và $\widehat{\mathrm{yPb}}$ là hai góc kề bù Px là tia phân giác của $\widehat{\mathrm{aPy}}$ Pz là tia phân giác của $\widehat{\mathrm{yPb}}$
KL	$\widehat{\mathrm{xPz}}$ là góc vuông

Vì Px là tia phân giác của $\widehat{\mathrm{aPy}}$ nên $\widehat{\mathrm{xPy}}=\frac{1}{2}\widehat{\mathrm{aPy}}$  

Vì Pz là tia phân giác của $\widehat{\mathrm{yPb}}$ nên $\widehat{\mathrm{yPz}}=\frac{1}{2}\widehat{\mathrm{yPb}}$ 

Nên $\widehat{\mathrm{xPy}}+\widehat{\mathrm{yPz}}=\frac{1}{2}\widehat{\mathrm{aPy}}+\frac{1}{2}\widehat{\mathrm{yPb}}=\frac{1}{2}\left(\widehat{\mathrm{aPy}}+\widehat{\mathrm{yPb}}\right)$

Mà ta có: $\widehat{\mathrm{aPy}}$ + $\widehat{\mathrm{yPb}}$ = 180° (hai góc kề bù)

Do đó: $\widehat{\mathrm{xPy}}+\widehat{\mathrm{yPz}}=\frac{1}{2}\cdot 180°=90°$

Mặt khác: $\widehat{\mathrm{xPy}}+\widehat{\mathrm{yPz}}=\widehat{\mathrm{xPz}}$

Vậy $\widehat{\mathrm{xPz}}=90°$, tức là $\widehat{\mathrm{xPz}}$ là góc vuông.

B2. Bài tập trắc nghiệm

Bài 1. Ta có a, b phân biệt; nếu a // c và b // c thì:

A. $\mathrm{a}\perp \mathrm{b}$;                                                                     

B. $\mathrm{a}\equiv \mathrm{b}$;

C. $\mathrm{a}\cap \mathrm{b}$;                                                                            

D. a // b.

Hướng dẫn giải

Đáp án đúng là: D

Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.

Bài 2. Tia Ot nào trong các hình dưới đây là tia phân giác của góc xOy.

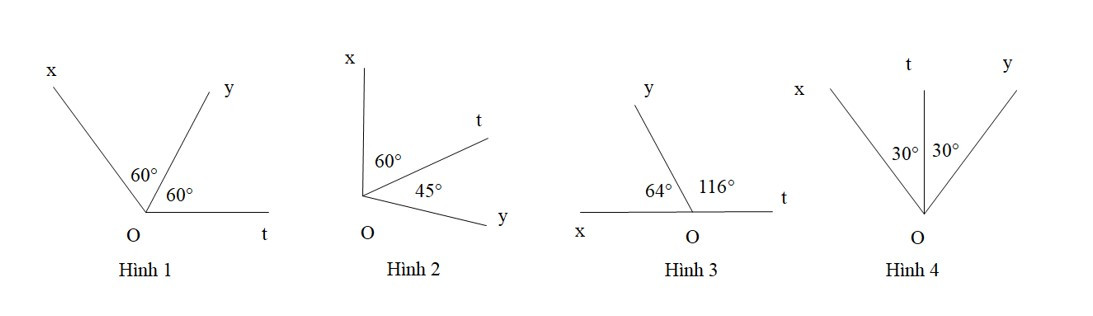
A. Hình 1;                                                                           

B. Hình 2;                                                                           

C. Hình 3;                                                                           

D. Hình 4.

Hướng dẫn giải

Đáp án đúng là: D

Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.

Hình 1 và hình 3 tia Ot không nằm trong góc nên tia Ot không phải tia phân giác của góc xOy.

Hình 2 có tia Ot nằm trong góc nhưng không tạo với hai cạnh của góc đó hai góc bằng nhau nên tia Ot trong hình 2 không phải tia phân giác của góc xOy.

Chỉ có hình 4 là tia Ot nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau nên Ot là tia phân giác của góc xOy.

Do đó chọn phương án D.

Bài 3. Cho tia Ot nằm trong góc mOn, $\widehat{\mathrm{mOt}}=\widehat{\mathrm{tOn}}$ thì

A. Ot là tia phân giác của góc mOn;                                  

B. Ot là tia nằm phía trong của góc mOn;                  

C. Ot là tia nằm phía ngoài của góc mOn;                         

D. Ot là tia nằm giữa hai cạnh Om và On.

Hướng dẫn giải

Đáp án đúng là: A

Ot là tia nằm trong góc mOn và tạo với hai cạnh của góc đó hai góc $\widehat{\mathrm{mOt}}=\widehat{\mathrm{tOn}}$ nên Ot là tia phân giác của góc mOn.

Do đó chọn đáp án A.

Bài 4. Tìm số đo x:

 

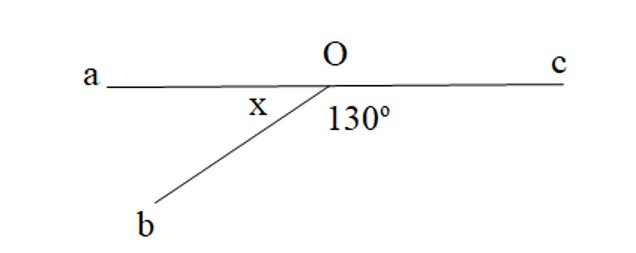
A. 65°;                                                                                

B. 120°;                                                                              

C. 95°;                                                                                

D. 50°.

Hướng dẫn giải

Đáp án đúng là: D

Ta có góc aOb và góc bOc là hai góc kề bù nên $\widehat{\mathrm{aOb}}+\widehat{\mathrm{bOc}}=180°$.

Suy ra $\mathrm{x}=\widehat{\mathrm{aOb}}=180°-\widehat{\mathrm{bOc}}=180°-130°=50°$.

Vậy x = 50^o.

Bài 5. Cho hình vẽ:

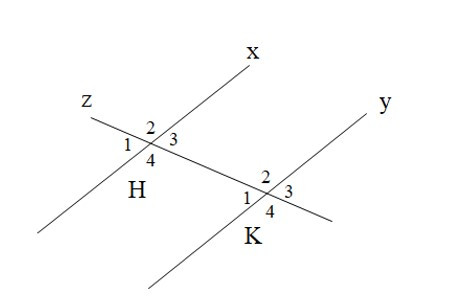
Biết x // y, $\widehat{{\mathrm{H}}_3}=39°.$Tính $\widehat{{\mathrm{H}}_3}+\widehat{{\mathrm{K}}_4}$.

A. 180°;                                                                              

B. 141°;                                                                              

C. 120°;                                                                              

D. 138°.

Hướng dẫn giải

Đáp án đúng là: A

Vì x // y nên suy ra $\widehat{{\mathrm{H}}_3}$ và $\widehat{{\mathrm{K}}_3}$ là hai góc đồng vị $\Rightarrow \widehat{{\mathrm{K}}_3}=\widehat{{\mathrm{H}}_3}=39°$ (1)

Mà $\widehat{{\mathrm{K}}_3}$ và $\widehat{{\mathrm{K}}_4}$là hai góc kề bù nên   $\Rightarrow \widehat{{\mathrm{K}}_3}+\widehat{{\mathrm{K}}_4}=180°$ (2)

Từ (1) và (2) $\Rightarrow \widehat{{\mathrm{H}}_3}+\widehat{{\mathrm{K}}_4}=180°$

Vậy $\Rightarrow \widehat{{\mathrm{H}}_3}+\widehat{{\mathrm{K}}_4}=180°$.

Bài 6. Chọn đáp án đúng.

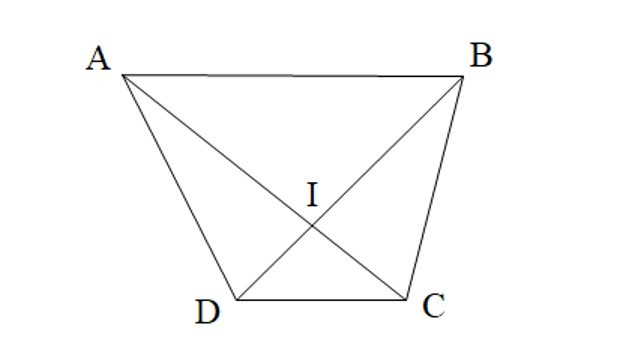
A. $\widehat{\mathrm{AID}}$ và  $\widehat{\mathrm{CIB}}$ là hai góc kề bù;                                       

B. $\widehat{\mathrm{ABC}}$  và  $\widehat{\mathrm{ADC}}$ là hai góc kề bù;                                   

C. $\widehat{\mathrm{AIB}}$  và  $\widehat{\mathrm{BIC}}$ là hai góc kề bù;                                      

D. $\widehat{\mathrm{AIB}}$  và  $\widehat{\mathrm{DIC}}$ là hai góc kề bù.

Hướng dẫn giải

Đáp án đúng là: C

$\widehat{\mathrm{AID}}$ và  $\widehat{\mathrm{CIB}}$ là hai góc hai góc kề bù (sai, vì $\widehat{\mathrm{AID}}$ và  $\widehat{\mathrm{CIB}}$ là hai góc hai góc đối đỉnh loại phương án A);

$\widehat{\mathrm{ABC}}$  và  $\widehat{\mathrm{ADC}}$ là hai góc kề bù (sai, vì $\widehat{\mathrm{ABC}}$  và  $\widehat{\mathrm{ADC}}$ là hai góc của tứ giác ABCD, loại phương án B);

$\widehat{\mathrm{AIB}}$  và  $\widehat{\mathrm{BIC}}$ là hai góc kề bù (đúng, chọn phương án C);

$\widehat{\mathrm{AIB}}$  và  $\widehat{\mathrm{DIC}}$ là hai góc kề bù (sai, vì $\widehat{\mathrm{AIB}}$  và  $\widehat{\mathrm{DIC}}$ là hai góc đối đỉnh, loại phương án D).

Bài 7. Cho hình vẽ bên dưới. Tính số đo góc OHC, biết MN // BC và $\widehat{\mathrm{AOM}}=59°$

A. 69°;                                                                                

B. 121°;                                                                              

C. 59°;                                                                                

D. 130°.

Hướng dẫn giải

Đáp án đúng là: B

Do MN // BC nên góc AOM và góc OHB là hai góc đồng vị do đó $\widehat{\mathrm{AOM}}=\widehat{\mathrm{OHB}}=59°$(1).

Lại có, góc OHB và góc OHC là hai góc kề bù nên $\widehat{\mathrm{OHB}}+\widehat{\mathrm{OHC}}=180°$(2).

Từ (1) và (2) suy ra $\widehat{\mathrm{OHC}}=180°-59°=121°$.

Vậy $\widehat{\mathrm{OHC}}=121°$.

Bài 8. Tính số đo của góc aOb. Biết $\widehat{\mathrm{zOb}}=48°$, Oz là tia phân giác của góc aOb.

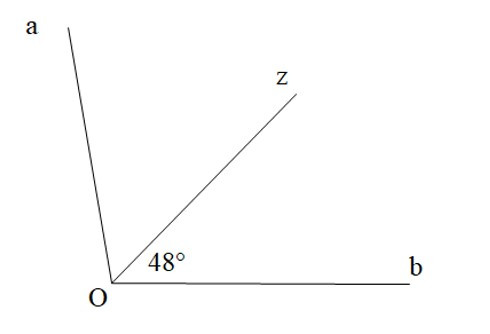
A. 80°;                                                                                

B. 96°;                                                                                

C. 120°;                                                                              

D. 130°.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: $\widehat{\mathrm{aOz}}=\widehat{\mathrm{zOb}}=48°$ (vì Oz là tia phân giác góc xOy)

Suy ra $\widehat{\mathrm{aOb}}=\widehat{\mathrm{aOz}}+\widehat{\mathrm{zOb}}=48°+48°=96°$.

Vậy $\widehat{\mathrm{aOb}}=96°$.

Bài 9. Cho hình vẽ như bên dưới. Tính $\widehat{{\mathrm{M}}_3}$, biết $\widehat{{\mathrm{N}}_2}=137°$.

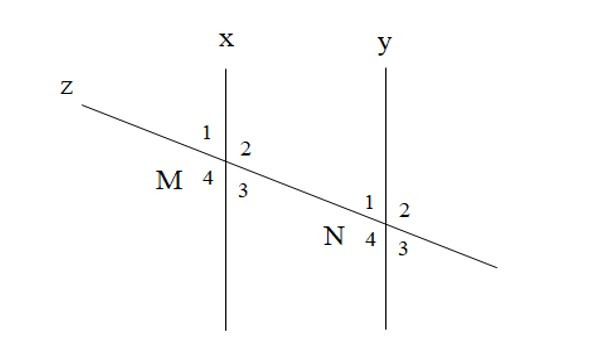
A. 137^o                                                                               

B. 43^o;                                                                                

C. 37^o;                                                                                

D. 149^o.

Hướng dẫn giải

Đáp án đúng là: B

Ta có $\widehat{{\mathrm{M}}_3}$ và $\widehat{{\mathrm{N}}_1}$ là hai góc so le trong suy ra $\widehat{{\mathrm{M}}_3}=\widehat{{\mathrm{N}}_1}$(1)

Lại có $\widehat{{\mathrm{N}}_1}$ và $\widehat{{\mathrm{N}}_2}$ là hai góc kề bù suy ra $\widehat{{\mathrm{N}}_1}+\widehat{{\mathrm{N}}_2}=180°$(2)

Từ (1) và (2) suy ra $\widehat{{\mathrm{M}}_3}+\widehat{{\mathrm{N}}_2}=180°\Rightarrow \widehat{{\mathrm{M}}_3}=180°-137°=43°$

Vậy $\widehat{{\mathrm{M}}_3}=43°$.

Bài 10. Điền vào chỗ trống nội dung phù hợp.

A. kết luận;                                                                         

B. khẳng định;                                                                    

C. chứng minh;                                                                   

D. Cả 3 đáp án đều đúng.

Hướng dẫn giải

Đáp án đúng là: A

Phần nằm giữa từ “Nếu” và từ “thì” là phần giả thiết vậy phần nằm sau từ “thì” là phần kết luận.

Vậy chọn đáp án A.

Bài 11. Phát biểu định lí sau bằng lời.

Giả thiết	t cắt m tại A, t cắt n tại B $\widehat{{\mathrm{A}}_1}$ và $\widehat{{\mathrm{B}}_1}$ là hai góc đồng vị $\widehat{{\mathrm{A}}_1}=\widehat{{\mathrm{B}}_1}$
Kết luận	m // n

A. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng m, n vuông góc với nhau;                                 

B. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng m, n song song với nhau;                                         

C. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng m, n song song với nhau;                              

D. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng m, n vuông góc với nhau.

Hướng dẫn giải

Đáp án đúng là: B

Nếu một đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng m, m song song với nhau.

Vậy chọn đáp án B.

Bài 12. Cho định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.

Hình vẽ minh hoạ cho định lí trên là:

A. Hình 1, Hình 2;

B. Hình 2, Hình 3;                                                      

C. Hình 3, Hình 4;                                                              

D. Hình 1, Hình 3.

Hướng dẫn giải

Đáp án đúng là: D

Hình 2 không thỏa mãn điều kiện hai đường thẳng song song nên loại phương án A, B.

Hình 4 không thỏa mãn điều kiện vuông góc với một trong hai đường thẳng nên loại phương án C.

Hình 1, 3 thỏa mãn cả hai điều kiện trên.

Vậy chọn phương án D.

====== ****&**** =====