Lý thuyết Toán lớp 7 Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết
A. Lý thuyết Hai đường thẳng song song và dấu hiệu nhận biết
1. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
• Cho đường thẳng c cắt hai đường thẳng a và b lần lượt tại A và B tạo thành bốn góc đỉnh A và bốn góc đỉnh B. Khi đó ta có:
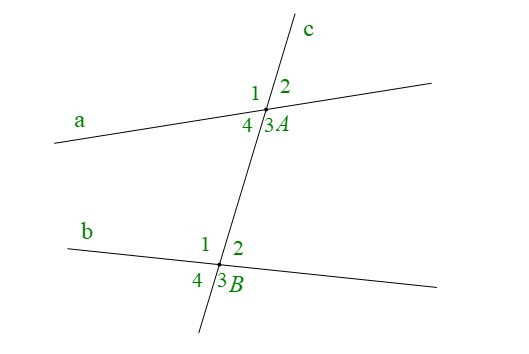
+ Các cặp góc so le trong là: A3 và B1; A4 và B2.
+ Các cặp góc đồng vị là: A1 và B1; A2 và B2; A3 và B3; A4 và B4.
+ Các cặp góc trong cùng phía là: A4 và B1; A3 và B2.
• Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+ Hai góc so le trong còn lại bằng nhau.
+ Hai góc đồng vị bằng nhau.
Ví dụ:
+ Cho đường thẳng c cắt hai đường thẳng phân biệt a, b lần lượt tại A và B.
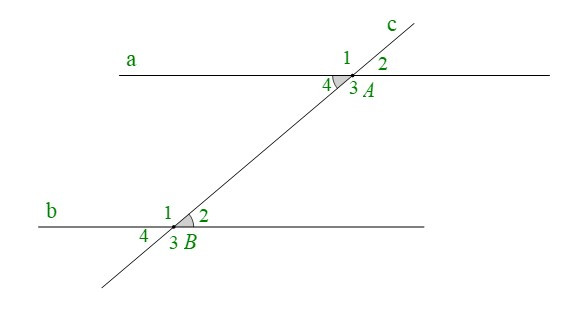
Ta có là cặp góc so le trong
Nếu thì cặp góc so le trong còn lại và các cặp góc đồng vị bằng nhau:
2. Dấu hiệu nhận biết hai đường thẳng song song
• Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a và b song song với nhau. Kí hiệu là: .
• Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Ví dụ:
+ Cho hình vẽ:
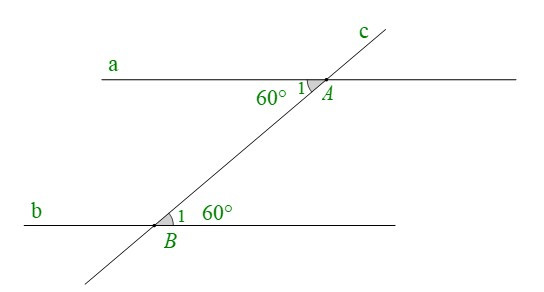
Ta có: . Mà hai góc ở vị trí so le trong.
Do đó: (dấu hiệu nhận biết hai đường thẳng song song).
+ Cho hình vẽ:
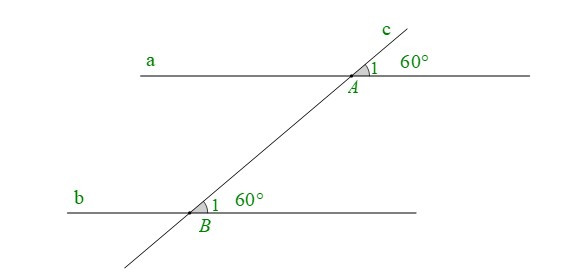
Ta có: . Mà hai góc ở vị trí đồng vị.
Do đó: (dấu hiệu nhận biết hai đường thẳng song song).
+ Cho hình vẽ:
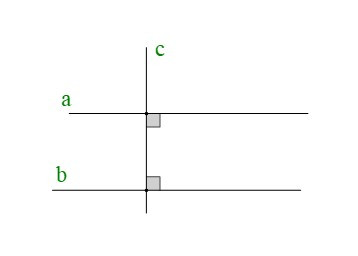
Ta có: và
Do đó: .
Chú ý:
+ Muốn vẽ đường thẳng đi qua một điểm và song song với một đường thẳng cho trước bằng góc 60° của êke ta làm như sau:
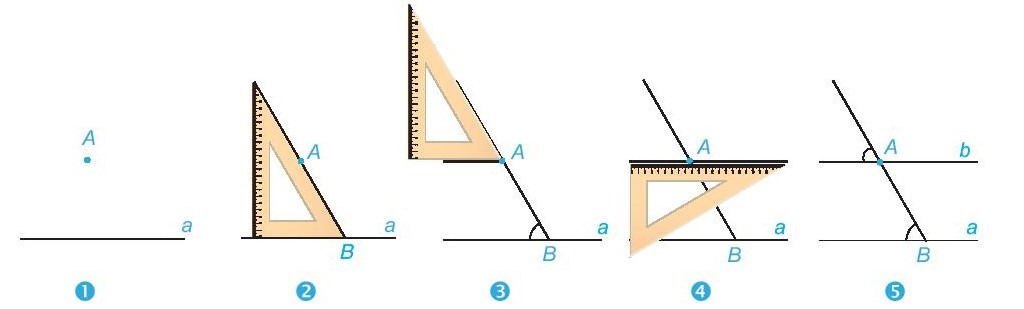
+ Tương tự ta có thể dùng góc vuông hoặc góc 30° của êke (thay cho góc 60°) để vẽ đường thẳng đi qua một điểm và song song với đường thẳng cho trước.
B. Bài tập tự luyện
B1. Bài tập tự luận
Bài 1. Cho hình vẽ:
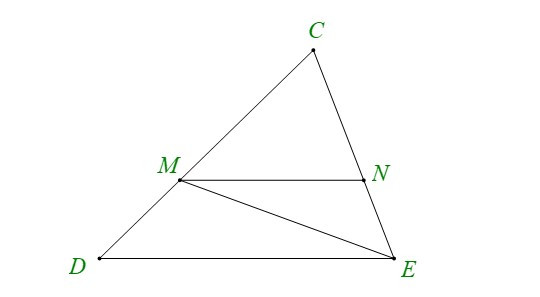
a) Tìm một góc ở vị trí so le trong với góc DEM.
b) Tìm một góc ở vị trí đồng vị với góc CMN.
c) Tìm một góc ở vị trí trong cùng phía với góc MNE.
Hướng dẫn giải
a) Có ME cắt MN và DE nên góc ở vị trí so le trong với góc DEM là góc EMN.
b) Có CD cắt MN và DE nên góc ở vị trí đồng vị với góc CMN là góc CDE (hay MDE).
c) Có CE cắt MN và DE nên góc ở vị trí trong cùng phía với góc MNE là góc NED (hay CED).
Bài 2. Cho các hình dưới đây, hãy giải thích tại sao .
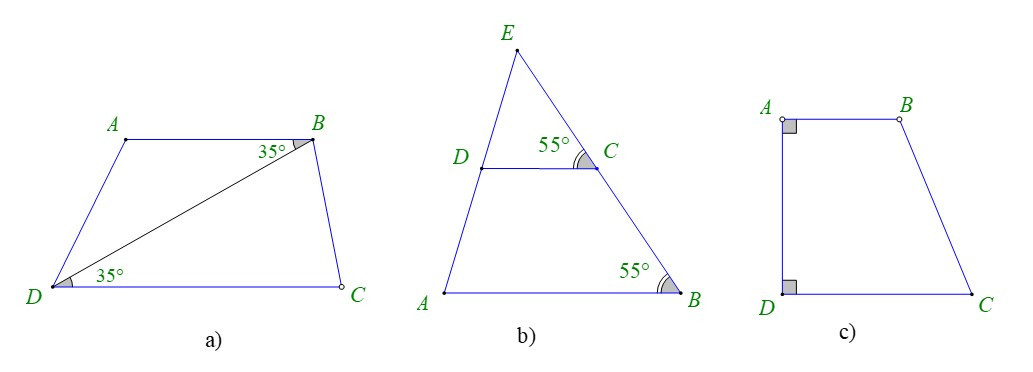
Hướng dẫn giải
a) Ta có:
Mà hai góc ở vị trí so le trong.
Do đó (dấu hiệu nhận biết hai đường thẳng song song).
b) Ta có:
Mà hai góc ở vị trí đồng vị.
Do đó (dấu hiệu nhận biết hai đường thẳng song song).
c) Ta có: và
Do đó: (dấu hiệu nhận biết hai đường thẳng song song).
Bài 3. Hãy vẽ hai đoạn thẳng AB và MN sao cho và .
Hướng dẫn giải
+ Vẽ đoạn thẳng AB với độ dài bất kì.
+ Dùng góc của êke vẽ tiếp theo các bước dưới đây.
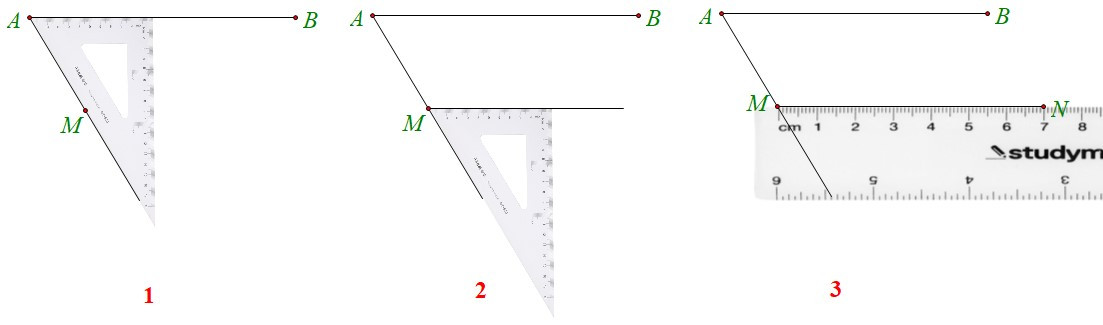
+ Ta được và .
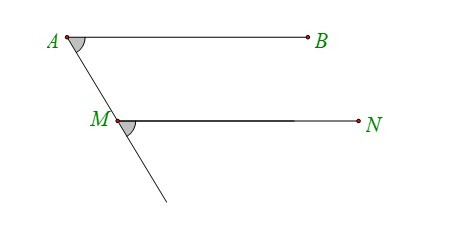
B2. Bài tập trắc nghiệm
Bài 4. Cho hình vẽ
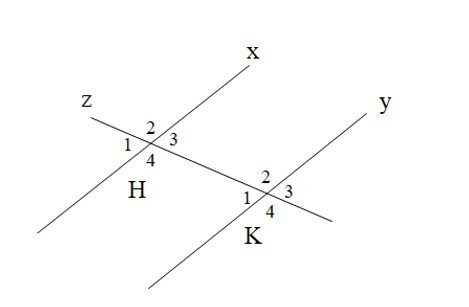
Biết x // y, Tính .
A. 180°;
B. 141°;
C. 120°;
D. 138°.
Hướng dẫn giải
Đáp án đúng là: A
Vì x // y nên suy ra và là hai góc đồng vị (1)
Mà và là hai góc kề bù nên (2)
Từ (1) và (2)
Vậy
Bài 5. Cho tia Ot nằm trong góc mOn, thì
A. Ot là tia phân giác của góc mOn;
B. Ot là tia nằm phía trong của góc mOn;
C. Ot là tia nằm phía ngoài của góc mOn;
D. Ot là tia nằm giữa hai cạnh Om và On.
Hướng dẫn giải
Đáp án đúng là: A
Ot là tia nằm trong góc mOn và tạo với hai cạnh của góc đó hai góc nên Ot là tia phân giác của góc mOn.
Do đó chọn đáp án A.
Bài 6. Tính số đo của góc aOb. Biết , Oz là tia phân giác của góc aOb.
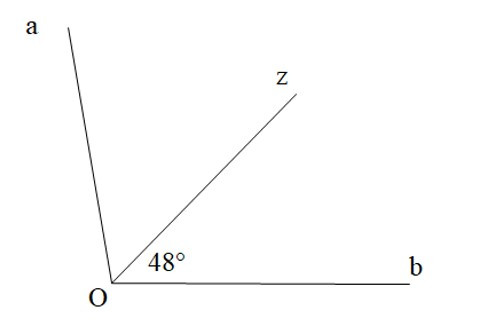
A. 80°;
B. 96°;
C. 120°;
D. 130°.
Hướng dẫn giải
Đáp án đúng là: B
Ta có: (vì Oz là tia phân giác góc xOy)
Suy ra .
Vậy .
====== ****&**** =====