Khoảng cách từ một điểm trên mặt phẳng đáy tới mặt phẳng chứa đường cao

Tài liệu Khoảng cách từ một điểm trên mặt phẳng đáy tới mặt phẳng chứa đường cao gồm các nội dung chính sau:

I. Phương pháp giải

–  Xét bài toán cụ thể và lời giải chi tiết

II. Ví dụ minh họa

– Gồm 7 ví dụ minh họa đa dạng của dạng bài trên và phương pháp giải chi tiết.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

KHOẢNG CÁCH TỪ MỘT ĐIỂM TRÊN MẶT PHẲNG ĐÁY TỚI MẶT PHẲNG CHỨA ĐƯỜNG CAO

I.   Phương pháp giải

Xét bài toán: Cho hình chóp có đỉnh S có hình chiếu vuông góc lên mặt đáy là H. Tính

khoảng cách từ điểm A bất kì đến mặt bên (SHB )                                                   .

Kẻ AH $\perp$HB ta có:

$\left\{\begin{array}{l}\mathrm{AK}\perp \mathrm{HB}\\ \mathrm{AK}\perp \mathrm{SH}\end{array}\right.\Rightarrow \mathrm{AK}\perp \left(\mathrm{SHB}\right)$

Suy ra d ( A;(SHB)) = AK .

Cách tính: Ta có: d ( A;(SHB)) = AK = $\frac{2{\mathrm{S}}_{\mathrm{ABC}}}{\mathrm{HB}}$ = AB sin·ABK = AH.sin AHK .

II.  Ví dụ minh họa

Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác ABC có  AB = 3a, BC = 2a, ·ABC = 60° . Biết SA $\perp$( ABC ) .

a)   Tính khoảng cách từ C đến mặt phẳng (SAB ) .

b)  Tính khoảng cách từ B đến mặt phẳng (SAC ) .

Lời giải

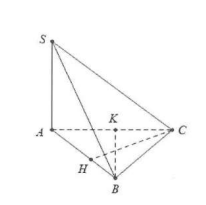
a, Dựng $\text{CH⊥AB ta có: }\left\{\begin{array}{l}\mathrm{CH}\perp \mathrm{AB}\\ \mathrm{CH}\perp \mathrm{SA}\end{array}\right.\Rightarrow \mathrm{CH}\perp \left(\mathrm{SAB}\right)$

Do đó d (C;(SAB)) = CH = CB sin ·ABH = 2a sin 60° = a $\sqrt{3}$ .

b, Dựng $\mathrm{CK}\perp \mathrm{AC} \Rightarrow \mathrm{CK}\perp \left(\mathrm{SAC}\right)$

Ta có:  d (B;(SAC )) = CH = $\frac{2{\mathrm{S}}_{\mathrm{ABC}}}{\mathrm{AC}}=\frac{\mathrm{AB}.\mathrm{BC}. \mathrm{sinABC}}{\mathrm{AC}}$

Trong đó: 

${\mathrm{AC}}^2={\mathrm{AB}}^2+{\mathrm{BC}}^2–2\mathrm{AB}.\mathrm{BC}.\cos \mathrm{B}\Rightarrow \mathrm{AC}=\mathrm{a}\sqrt{7}\Rightarrow \mathrm{d}\left(\mathrm{B},\left(\mathrm{SAC}\right)\right)=\frac{3\mathrm{a}.2\mathrm{a} \sin {60}^{\mathrm{o}}}{\mathrm{a}\sqrt{7}}=\frac{3\mathrm{a}\sqrt{7}}{7}$

Ví dụ 2: Cho hình chóp S.ABCD có đáy là hình chữ nhật với \[B = a,AD = a\sqrt 3 \]. Tam giác SAB cân tại S và thuộc mặt phẳng vuông góc với đáy. Gọi H là trung tâm của AB. a) Tính khoảng cách từ A đến mặt phẳng \[\left( {SHD} \right)\]. b) Tính khoảng cách từ D đến mặt phẳng \[\left( {SHC} \right)\].

 

Lời giải

a) Do tam giác SAB cân tại S nên \[SH \bot AB\].

Ta có: \[HA = HD = \frac{a}{2}\].

Mặt khác \[\left( {SAB} \right) \bot \left( {ABCD} \right) \Rightarrow SH \bot \left( {ABCD} \right)\].

Dựng

 \[\begin{array}{l}AE \bot DH \Rightarrow AE \bot \left( {SHD} \right)\\ \Rightarrow d\left( {A;\left( {SHD} \right)} \right) = AE\end{array}\].

Mặt khác \[AE = \frac{{AH.AD}}{{\sqrt {A{H^2} + A{D^2}} }} = \frac{{a\sqrt {39} }}{{13}}\].

b) Dựng \[DK \bot CH \Rightarrow d\left( {D;\left( {SHC} \right)} \right) = DK\].

Ta có:

\[CH = \sqrt {H{B^2} + B{C^2}}  = \frac{{a\sqrt {13} }}{2}\], \[{S_{HCD}} = \frac{1}{2}CD.d\left( {H;CD} \right) = \frac{1}{2}{\rm{.}}a{\rm{.}}a\sqrt 3  = \frac{{{a^2}\sqrt 3 }}{2}\].

Do đó \[d\left( {D;\left( {SHC} \right)} \right) = \frac{{2{S_{HCD}}}}{{CH}} = \frac{{2a\sqrt {39} }}{{13}}\].

 

Ví dụ 3: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B có \[AD = 3a\], \[AB = BC = 2a\]. Biết \[SA \bot \left( {ABCD} \right)\]. a) Tính khoảng cách từ C đến mặt phẳng \[\left( {SAD} \right)\]. b) Tính khoảng cách từ D đến mặt phẳng \[\left( {SAC} \right)\].

Lời giải

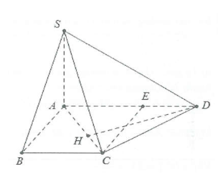
a) Dựng \[CE \bot AD \Rightarrow CE \bot \left( {SAD} \right)\].

Khi đó \[d\left( {C;\left( {SAD} \right)} \right) = CE\], do ABCE là hình vuông cạnh \[2a\] nên \[CE = AE = 2a \Rightarrow d\left( {C;\left( {SAD} \right)} \right) = 2a\].

b) Dựng \[DH \bot AC \Rightarrow DH \bot \left( {SAC} \right)\].

Khi đó \[d\left( {D;\left( {SAC} \right)} \right) = DH\].

Ta có: ABCE là hình vuông nên \[\widehat {CAD} = 45^\circ \].

Do đó \[DH = ADsin45^\circ  = 3a.\frac{{\sqrt 2 }}{2} = \frac{{3a\sqrt 2 }}{2}\].

 

Ví dụ 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \[5a\]. Hình chiếu vuông góc của đỉnh S trên mặt phẳng \[\left( {ABCD} \right)\] trùng với trọng tâm H của tam giác ABD. a) Tính khoảng cách từ B đến mặt phẳng \[\left( {SAC} \right)\]. b) Tính khoảng cách từ C đến mặt phẳng \[\left( {SHD} \right)\].

Lời giải

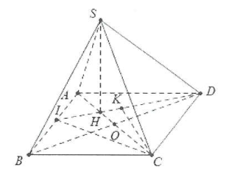
a) Do H là trọng tâm tam giác ABD \[ \Rightarrow H \in AC\].

Gọi O là tâm của hình vuông ABCD \[ \Rightarrow BO \bot AC\].

Mặt khác \[BO \bot SH \Rightarrow BO \bot \left( {SAC} \right)\]

Khi đó \[d\left( {B;\left( {SAC} \right)} \right) = BO = \frac{{5a\sqrt 2 }}{2}\].

b) Dựng

 \[\begin{array}{l}CK \bot HD \Rightarrow CK \bot \left( {SHD} \right)\\ \Rightarrow d\left( {C;\left( {SHD} \right)} \right) = CK\end{array}\].

Gọi I là trung điểm của AB thì \[H = DI \cap AO\].

Khi đó:

 \[\begin{array}{l}CK = \frac{{2{S_{ICD}}}}{{DI}} = \frac{{2.\frac{1}{2}{S_{ABCD}}}}{{DI}}\\ = \frac{{25{a^2}}}{{\sqrt {D{A^2} + A{I^2}} }} = \frac{{25{a^2}}}{{\sqrt {25{a^2} + {{\left( {\frac{{5a}}{2}} \right)}^2}} }}\\ = 2a\sqrt 5 \end{array}\].

 

Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD nửa lục giác đều cạnh \[a\], với \[AB = 2a\]. Biết \[SA \bot \left( {ABCD} \right)\] và mặt phẳng \[\left( {SBC} \right)\] tạo với đáy một góc \[60^\circ \]. a) Tính khoảng cách từ C đến mặt phẳng \[\left( {SAB} \right)\]. b) Tính khoảng cách từ D đến mặt phẳng \[\left( {SAC} \right)\].

Lời giải

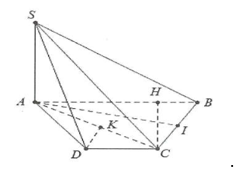
a) Tứ giác ABCD là nửa lục giác đều cạnh \[a\] nên nó nội tiếp đường tròn đường kính \[AB = 2a\].

Dựng

 \[\begin{array}{l}CH \bot AB \Rightarrow CH \bot \left( {SAB} \right)\\ \Rightarrow d\left( {C;\left( {SAB} \right)} \right) = CH\end{array}\].

Mặt khác \[\widehat {ABC} = 60^\circ \]\[ \Rightarrow CH = BC\sin 60^\circ  = \frac{{a\sqrt 3 }}{2}\]

Vậy \[d\left( {C;\left( {SAB} \right)} \right) = \frac{{a\sqrt 3 }}{2}\].

b) Dựng \[DK \bot AC \Rightarrow DK \bot \left( {SAC} \right) \Rightarrow d\left( {D;\left( {SAC} \right)} \right) = DK\].

Do

 \[\begin{array}{l}\widehat {DCB} = 120^\circ ,\widehat {ACB} = 90^\circ \\ \Rightarrow \widehat {ACD} = 30^\circ \\ \Rightarrow DK = CD\sin \widehat {DCK}\\ = a\sin 30^\circ  = \frac{a}{2}\end{array}\].

 

Ví dụ 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có diện tích bằng 2, \[AB = \sqrt 2 ,BC = 2\]. Gọi M là trung điểm của CD, hai mặt phẳng \[\left( {SBD} \right)\] và \[\left( {SAM} \right)\] cùng vuông góc với đáy. Tính khoảng cách từ B đến mặt phẳng \[\left( {SAM} \right)\].

 

Lời giải

Ta có

 \[\begin{array}{l}{S_{ABCD}} = 2{S_{\Delta ABC}} = 2{S_{\Delta MAB}} = 2\\ \Rightarrow {S_{\Delta ABC}} = {S_{\Delta MAB}} = 1\end{array}\].

\[\begin{array}{l} \Rightarrow {S_{\Delta ABC}} = \frac{1}{2}.AB.BC.\sin \widehat {ABC} = 1\\ \Rightarrow \sin \widehat {ABC} = \frac{1}{{\sqrt 2 }}\end{array}\].

Do đó \[\widehat {ABC} = 45^\circ  \Rightarrow \widehat {ADM} = 45^\circ \].

Áp dụng định lý Cosin trong tam giác ADM, ta có:

\[AM = \sqrt {A{D^2} + D{M^2} – 2.AD.DM.cos\widehat {ADM}}  = \frac{{\sqrt {10} }}{2}\]

Gọi H là giao điểm của AM và BD \[ \Rightarrow SH \bot \left( {ABCD} \right)\].

Kẻ BK vuông góc với AM, \[K \in AM \Rightarrow BK \bot AM\] \[\left( 1 \right)\].

Ta có

 \[\begin{array}{l}\left( {SAM} \right) \cap \left( {SBD} \right) = SH\\ \Rightarrow SH \bot \left( {ABCD} \right) \Rightarrow SH \bot BK\end{array}\] \[\left( 2 \right)\].

Từ \[\left( 1 \right)\],\[\left( 2 \right)\]\[ \Rightarrow BK \bot \left( {SAM} \right) \Rightarrow d\left( {B;\left( {SAM} \right)} \right) = BK\].

Mặt khác

 \[\begin{array}{l}{S_{\Delta MAB}} = \frac{1}{2}.BK.AM\\ \Rightarrow BK = \frac{{2.{S_{\Delta MAB}}}}{{AM}} = \frac{4}{{\sqrt {10} }} = \frac{{2\sqrt {10} }}{5}\end{array}\].

 

Ví dụ 7: Cho hình lăng trụ \[ABCD.A’B’C’D’\] có đáy là hình chữ nhật ABCD có hai đường chéo \[AC = BD = 2a\]. Tam giác A’BD vuông cân tại A’ và nằm trong mặt phẳng vuông góc với đáy. Mặt phẳng \[\left( {A’AB} \right)\] tạo với đáy một góc \[60^\circ \]. Tính khoảng cách \[d\left( {B’;\left( {A’BD} \right)} \right)\].

Lời giải

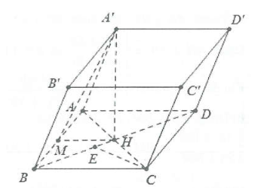
Gọi H là tâm hình chữ nhật ABCD

\[ \Rightarrow \]\[HA = HC \Rightarrow A’H \bot BD\] (Do \[\Delta A’BD\] cân tại A’).

Do \[\left( {A’BD} \right) \bot \left( {ABCD} \right) \Rightarrow A’H \bot \left( {ABCD} \right)\].

Ta có: \[A’H = \frac{1}{2}BD = a\] (trong tam giác vuông đường trung tuyến ứng cạnh huyền bằng nửa cạnh ấy).

Dựng

 

+) Khi đó: \[HM\tan 60^\circ  = A’H \Rightarrow HM = \frac{a}{{\sqrt 3 }}\]

\[ \Rightarrow AD = 2HM = \frac{{2a}}{{\sqrt 3 }} \Rightarrow AB = 2a\sqrt {\frac{2}{3}} \]

Do:

 \[\begin{array}{l}A’D//B’C \Rightarrow B’C//\left( {A’BD} \right)\\ \Rightarrow d\left( {B’;\left( {A’BD} \right)} \right) = d\left( {C;\left( {A’BD} \right)} \right)\end{array}\].

Ta có: \[CE = \frac{{CD.CB}}{{BD}} = \frac{{2a\sqrt 2 }}{3}\]. Vậy \[d\left( {B’;\left( {A’BD} \right)} \right) = \frac{{2a\sqrt 2 }}{3}\].

 

Xem thêm