Giải SBT Toán lớp 6 Bài 2: Tính chất cơ bản của phân số
Bài 1 trang 11 sách bài tập Toán lớp 6 Tập 2: Quy đồng mẫu số các phân số sau:
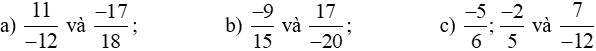
Lời giải:
a) 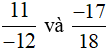
Ta có MSC = BCNN (12, 18) = 36.
Ta quy đồng như sau:
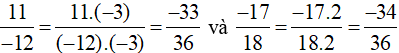
b) 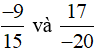
Ta có MSC = BCNN(15, 20) = 36.
Ta quy đồng như sau:
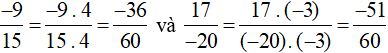
c) 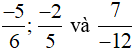
Ta có MSC = BCNN(6, 5, 12) = 60.
Ta quy đồng như sau:
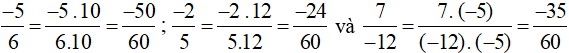
Bài 2 trang 12 sách bài tập Toán lớp 6 Tập 2: Viết các số sau thành các phân số có cùng mẫu số (chọn mẫu số chung là số dương nhỏ nhất nếu được).

Lời giải:
Ta thực hiện theo hai bước như sau:
Bước 1: Tìm mẫu số chung của hai phân số (là bội chung nhỏ nhất của các mẫu số).
Bước 2: Nhân cả tử và mẫu của mỗi phân số với số nguyên thích hợp (nhân tử phụ) để được phân số mới có mẫu là mẫu số chung.
a) 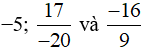
Ta có: 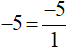
Vì BCNN(1, 20, 9) = BCNN(20, 9)
Để tìm mẫu số chung là số dương nhỏ nhất (hay là bội chung nhỏ nhất của các mẫu số) ta làm như sau:
+ Phân tích các số sau ra thừa số nguyên tố: 20 = 22.5 ; 9 = 32;
+ Thừa số nguyên tố chung và riêng là: 2; 3 và 5;
+ Số mũ lớn nhất của 2 là 2, số mũ lớn nhất của 3 là 2 và số mũ lớn nhất của 5 là 1.
+ BCNN (1; 20; 9) = 22.32.5 = 180.
Do đó mẫu số chung là số dương nhỏ nhất là 180.
Ta thực hiện:
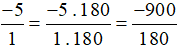

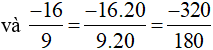
b) 
Ta có: 
Vì BCNN(15, 25, 1) = BCNN(15, 25)
Để tìm mẫu số chung là số dương nhỏ nhất (hay là bội chung nhỏ nhất của các mẫu số) ta làm như sau:
+ Phân tích các số sau ra thừa số nguyên tố: 15 = 3.5; 25 = 52;
+ Thừa số nguyên tố chung là 5 và riêng là 3;
+ Số mũ lớn nhất của 3 là 1 và số mũ lớn nhất của 5 là 2;
+ BCNN (1; 15; 25) = 3.52 = 75.
Do đó mẫu số chung là số dương nhỏ nhất là 75.
Ta thực hiện:

Bài 3 trang 12 sách bài tập Toán lớp 6 Tập 2: Rút gọn các phân số sau:

Lời giải:
Như đã từng tìm hiểu ở học kì I, khi rút gọn một phân số ta nên chia cả tử và mẫu của phân số đó cho ước chung lớn nhất của cả tử và mẫu để được phân số tối giản (hoặc có thể chia cả tử và mẫu của phân số đó cho ước chung khác 1 và khác −1).
a) Cách 1 (chia cả tử và mẫu cho ước chung khác 1 và −1):
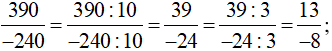
Cách 2 (chia cả tử và mẫu cho ước chung lớn nhất của cả tử và mẫu):

b) Cách 1(chia cả tử và mẫu cho ước chung khác 1 và −1):
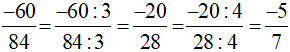
Cách 2 (chia cả tử và mẫu cho ước chung lớn nhất của cả tử và mẫu):
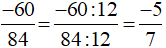
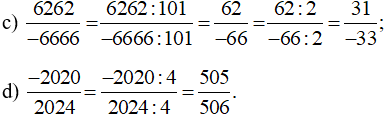
Bài 4 trang 12 sách bài tập Toán lớp 6 Tập 2: Hình vẽ sau minh hoạ tính chất nào của phân số?

Lời giải:
Trong hình a:
– Ở hình vẽ thứ nhất: hình chữ nhật được chia thành 5 phần bằng nhau, tô màu 2 phần. Nên phân số biểu thị số phần tô màu là 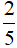 .
.
– Ở hình vẽ thứ hai: hình chữ nhật được chia thành 20 phần bằng nhau, tô màu 8 phần. Nên phân số biểu thị số phần tô màu là 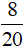 .
.
Do đó hai phân số thể hiện phần tô màu trong Hình a là 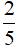 và
và 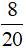 .
.
Vì 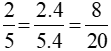 nên hình a minh hoạ tính chất 1 (Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho).
nên hình a minh hoạ tính chất 1 (Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho).
Trong hình b:
– Ở hình vẽ thứ nhất: có 5 hình tròn bằng nhau, mỗi hình tròn chia thành 3 phần bằng nhau. Trong hình trên chia thành 15 phần, tô màu 12 phần. Nên phân số biểu thị số phần tô màu là  .
.
– Ở hình vẽ thứ hai: có 5 hình tròn bằng nhau, tô màu 4 hình. Nên phân số biểu thị số phần tô màu là  .
.
Do đó hai phân số biểu thị phần tô màu trong hình b là  và
và  .
.
Vì  nên hình b minh hoạ tính chất 2 (Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho).
nên hình b minh hoạ tính chất 2 (Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho).
Bài 5 trang 12 sách bài tập Toán lớp 6 Tập 2: Nêu hai cách giải thích các phân số sau bằng nhau (dùng khái niệm bằng nhau và dùng tính chất).

Lời giải:
Cách 1: Dùng khái niệm bằng nhau:
Nếu a . d = b . c thì 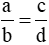 (với a, b, c, d ≠ 0).
(với a, b, c, d ≠ 0).
Cách 2: Dùng tính chất:
– Tính chất 1: Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được phân số bằng phân số đã cho.
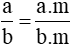 , với m ∈ Z và m ≠ 0.
, với m ∈ Z và m ≠ 0.
– Tính chất 2: Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.
 , với n ∈ ƯC (a; b).
, với n ∈ ƯC (a; b).
a) Cách 1 (dùng định nghĩa): vì (−15) . (−11) = 5 . 33 =165 nên  .
.
Vậy 
Cách 2 (dùng tính chất 2): Ta có  .
.
Vậy 
b) Cách 1 (dùng định nghĩa): Vì 7 . (−60) = (−12) . 35 = −420 nên  .
.
Vậy  .
.
Cách 2 (dùng tính chất 1): Ta có:
Vậy 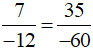 .
.
c) Cách 1 (dùng định nghĩa): Vì (−8) . (−21) = 14 . 12 = 168 nên 
Vậy 
Cách 2 (dùng tính chất 2 và tính chất 1): Ta có:
Vậy 
Bài 6 trang 12 sách bài tập Toán lớp 6 Tập 2: Dùng phân số để viết các đại lượng khối lượng sau theo tạ, theo tấn.
a) 223 kg;
b) 18 kg;
c) 2020 kg;
d) 7 kg.
Lời giải:
Các đơn vị đo khối lượng sắp xếp theo thứ tự từ lớn đến bé lần lượt là: tấn, tạ, yến, kg, hg, dag, g. Mỗi đơn vị đo khối lượng đều gấp 10 lần đơn vị bé hơn, liền nó.
Ta có: 1 tạ = 100 kg, 1 tấn = 1 000 kg.
Khi đổi từ kg sang tạ, ta chia số đó cho 100 (viết dưới dạng phân số)
Khi đổi từ kg sang tấn, ta chia số đó cho 1000 (viết dưới dạng phân số).
Phân số để viết các đại lượng khối lượng theo tạ, theo tấn là:
a) 223 kg =  tạ
tạ
223 kg = 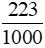 tấn.
tấn.
b) 18 kg = 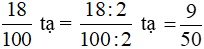 tạ;
tạ;
18 kg =  tấn.
tấn.
c) 2020 kg = 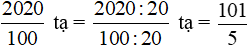 tạ;
tạ;
2020 kg = 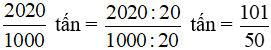 tấn.
tấn.
d) 7 kg =  tạ;
tạ;
7 kg = 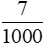 tấn.
tấn.
Bài 7 trang 12 sách bài tập Toán lớp 6 Tập 2: Dùng phân số với mẫu số dương nhỏ nhất để viết các đại lượng dung tích sau theo lít.
a) 600 ml;
b) 280 ml;
c) 1300 ml;
d) 970 ml.
Lời giải:
Nhận xét: 1 lít = 1000 ml.
Khi đổi từ ml sang lít, ta chia số đó cho 1000 (viết dưới dạng phân số).
Phân số với mẫu số dương nhỏ nhất để viết các đại lượng dung tích theo lít là:
a) 600 ml = 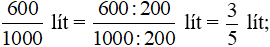
b) 280 ml = 
c) 1300 ml = 
d) 970 ml = 
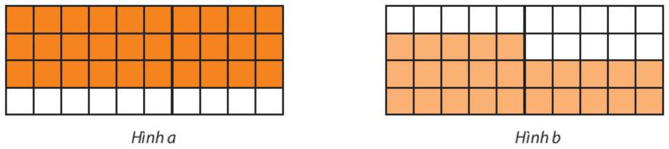
Bài 8 trang 12 sách bài tập Toán lớp 6 Tập 2: Dùng phân số với mẫu số dương nhỏ nhất để biểu thị phần tô màu trong mỗi hình vẽ sau:
Lời giải:
Để biểu thị phần tô màu trong hình vẽ bằng phân số với mẫu số dương nhỏ nhất ta thực hiện như sau:
Bước 1: Biểu thị phần tô màu trong hình vẽ bằng phân số.
Bước 2: Rút gọn phân số đó sao cho mẫu số thu được là số dương và nhỏ nhất (hay là rút gọn phân số đó về phân số tối giản có mẫu số dương).
Trong hình a là hình chữ nhật được chia thành 40 ô vuông, tô màu 30 ô vuông. Phân số biểu thị phần tô màu trong hình vẽ là 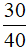 .
.
Rút gọn phân số về phân số tối giản có mẫu số dương: 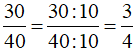
Vậy phân số với mẫu số dương nhỏ nhất để biểu thị phần tô màu trong mỗi hình a là  .
.
Trong hình b là hình chữ nhật được chia thành 40 ô vuông, tô màu 25 ô vuông. Phân số biểu thị phần tô màu trong hình vẽ là 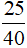 .
.
Rút gọn phân số về phân số tối giản có mẫu số dương: 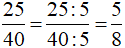 .
.
Vậy phân số với mẫu số dương nhỏ nhất để biểu thị phần tô màu trong mỗi hình a là 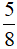 .
.
====== ****&**** =====