Giải SBT Toán lớp 6 Bài tập cuối chương 7
Bài 1 trang 77 sách bài tập Toán lớp 6 Tập 2: Vẽ thêm để các hình sau có trục đối xứng là đường nét đứt trên hình vẽ. Em hãy cho biết đó là hình gì.
a)

b)

Lời giải:
Coi đường nét đứt như một cái gương, vẽ thêm sao cho khi gập hình theo đường nét đứt ta được hai phần giống hệt và chồng khít lên nhau.
Hình sau khi được vẽ thêm có đường nét đứt là trục đối xứng.
Hình a)

Hình b)
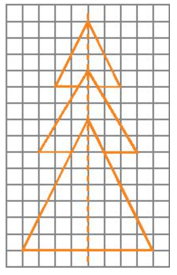
Hình a) là hình mặt người. Hình b) là hình cây thông.
Bài 2 trang 78 sách bài tập Toán lớp 6 Tập 2: Vẽ thêm để được hình có tâm đối xứng là các điểm cho sẵn.
a)

b)

c)

Lời giải:
Hình a)
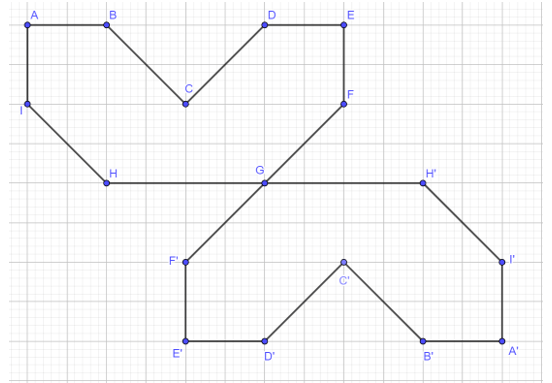
Đặt tên các đỉnh là A, B, C, D, E, F, G, H, I lần lượt như hình vẽ và G là tâm đối xứng:

Ta lấy các điểm A’, B’, C’, D’, E’, F’, H’, I’ lần lượt đối xứng với A, B, C, D, E, F, H, I qua G (như hình vẽ).

Nối các điểm lại ta được hình A’B’C’D’E’F’GH’I’ đối xứng với hình ABCDEFGHI qua tâm G (như hình vẽ).
Hình b)
Đặt tên các đỉnh là M, N, P, Q, R, S, U, O, X, Y lần lượt như hình vẽ và O là tâm đối xứng.

Ta thấy O là trung điểm UX, khi đó U đối xứng với X qua O.
Ta lấy các điểm M’, N’, P’, Q’, R’, S’, Y’ lần lượt đối xứng với M, N, P, Q, R, S, Y qua O (như hình vẽ).

Nối các điểm lại, ta được hình M’N’P’Q’R’S’XOUY’ đối xứng với hình MNPQRSXOUY qua tâm O (như hình vẽ).

Hình c)
Đặt tên các đỉnh là G, H, I, K, L, M, N, U, V lần lượt như hình vẽ và I là tâm đối xứng.

Ta thấy điểm H, K, M lần lượt đối xứng với điểm N, U, V qua điểm I.
Ta lấy các điểm G’, L’ lần lượt đối xứng với G, L qua I (như hình vẽ).

Nối các điểm lại, ta được hình G’NIUL’VHKM đối xứng với hình GHIKLMNUV qua tâm I (như hình vẽ).

Bài 3 trang 78 sách bài tập Toán lớp 6 Tập 2: Dưới đây là hình ảnh một số di tích ở Hà Nội. Em hãy tìm tính đối xứng và cho biết tên các di tích này.

Lời giải:
Cả hai hình đều có trục đối xứng và không có tâm đối xứng được biểu diễn như trên hình vẽ:
Hình a)

Hình b)

Hình a) là Khuê Văn Các, Hà Nội.
Hình b) là Nhà hát lớn Hà Nội.
Bài 4 trang 78 sách bài tập Toán lớp 6 Tập 2:
a) Dưới đây là một số hoa văn trang trí. Hãy chỉ ra tính đối xứng của chúng.

Lời giải:
a) Theo thứ tự từ trên xuống:
– Hình thứ nhất có trục đối xứng, không có tâm đối xứng.
– Hình thứ hai có tâm đối xứng, không có trục đối xứng.
– Hình thứ ba có trục đối xứng, không có tâm đối xứng.
b) Ba hoa văn khác có tính đối xứng.
Hình thứ nhất có trục đối xứng.

Hình thứ hai vừa có trục đối xứng vừa có tâm đối xứng.
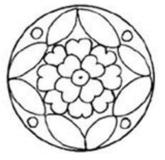
Hình thứ ba có trục đối xứng.

Bài 5 trang 78 sách bài tập Toán lớp 6 Tập 2: Chữ cái nào trong mỗi từ sau có tính đối xứng? Với mỗi từ, hãy nêu tên tỉnh thành tương ứng.
a) H O A B I N H;
b) N G H E A N;
c) B E N T R E;
d) B A C K A N;
e) Q U A N G T R I;
g) D A N A N G.
Lời giải:
Các chữ cái H, O, I vừa cí trục đối xứng vừa có tâm đối xứng..
Các chữ cái A, C, E, T, M, U có trục đối xứng.
Chữ cái N có tâm đối xứng.
Tên các tỉnh là:
a) Hòa Bình;
b) Nghệ An;
c) Bến Tre;
d) Bắc Kạn;
e) Quảng Trị;
g) Đà Nẵng.
Bài 6 trang 79 sách bài tập Toán lớp 6 Tập 2: Hình vỏ ốc và chiếc lá sau đây, hình nào có tính đối xứng? Hãy tìm ba hình động vật có tính đối xứng.

Lời giải:
Hình vỏ ốc không có tính đối xứng (không có trục đối xứng và không có tâm đối xứng).
Hình chiếc lá có tình đối xứng (có trục đối xứng).

Một số hình động vật có tính đối xứng:
Con cua có trục đối xứng

Con tôm hùm có trục đối xứng

Con bướm có trục đối xứng

Bài 7 trang 79 sách bài tập Toán lớp 6 Tập 2: Một số xe cứu thương có dòng chữ này dưới đây ở đầu xe. Dòng chữ này có nghĩa là gì? Tại sao lại có dòng chữ này ở đầu xe?

Lời giải:
Trục đối xứng như là một chiếc gương.
Nếu ta nhìn qua gương thì dòng chữ ở đầu xe sẽ qua trụ đối xứng và hiện trên gương là AMBULANCE có nghĩa là xe cứu thương. Dòng chữ ngược này xuất hiện ở đầu xe để người lái xe phía trước nhìn qua gương chiếu hậu biết đó là xe cứu thương để nhường đường.

Bài 8 trang 79 sách bài tập Toán lớp 6 Tập 2: Bàn cờ vua gồm 8 hàng (đánh số từ 1 đến 8) và 8 cột (đánh các chữ cái từ a đến h).
a) Tìm trục đối xứng và tâm đối xứng của bàn cờ vua.
b) Mã trắng nằm ở ô b1, hãy tìm quân cờ đối xứng với nó qua tâm đối xứng.
c) Vua trắng nằm ở ô e1, hãy tìm quân cờ đối xứng với nó qua trục đối xứng ngang (đường thẳng giữa hàng 4 và hàng 5).

Lời giải:
a) Bàn cờ vua có 4 trục đối xứng gồm: hai đường chéo của bàn cờ, trục ngang là đường thẳng giữa hàng 4 và 5, trục dọc là đường thẳng giữa cột d và cột e.
b) Mã trắng ở ô b1, có hình đối xứng qua tâm là mã đen ở ô g8.
c) Vua trắng ở ô e1, có hình đối xứng qua trục ngang (giữa hàng 4 và hàng 5) là vua đen ở ô e8.

====== ****&**** =====