Giải SBT Toán lớp 6 Bài 4: Đoạn thẳng. Độ dài đoạn thẳng
Bài 1 trang 93 sách bài tập Toán lớp 6 Tập 2: Hãy vẽ hình tương ứng trong mỗi trường hợp sau:
a) đoạn thẳng AB;
b) đường thẳng AB;
c) Tia AB;
d) Tia BA.
Lời giải:
a) Cách vẽ đoạn thẳng AB:
– Lấy hai điểm A và B bất kỳ.
– Nối điểm A với điểm B, ta được đoạn thẳng AB.
Ta có hình vẽ:

b) Cách vẽ đường thẳng AB:
– Lấy hai điểm A và B bất kỳ.
– Nối điểm A với điểm B, kéo dài về hai phía, ta được đường thẳng AB.
Ta có hình vẽ:

c) Cách vẽ tia AB:
– Lấy hai điểm A và B bất kỳ.
– Nối điểm A với điểm B, kéo dài qua điểm B, ta được tia AB.
Ta có hình vẽ:

d) Cách vẽ tia BA:
– Lấy hai điểm A và B bất kỳ.
– Nối điểm B với điểm A, kéo dài qua điểm A, ta được tia BA.
Ta có hình vẽ:

Bài 2 trang 93 sách bài tập Toán lớp 6 Tập 2: Hãy ước lượng để so sánh độ dài các đoạn thẳng AB và CD trong các hình dưới đây, sau đó dùng thước đo để kiểm tra lại.
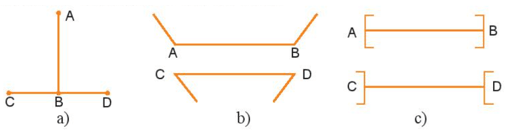
Lời giải:
Ước lượng bằng mắt sau đó kiểm tra lại bằng thước.
Hình a)
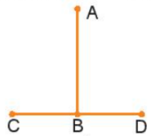
– Ước lượng bằng mắt, dự đoán: CD > AB.
– Dùng thước đo kiểm tra được: CD > AB.
Hình b)

– Ước lượng bằng mắt bằng cách dóng thẳng điểm điểm A với điểm C, điểm B với điểm D (như hình vẽ). Dự đoán: AB = CD.
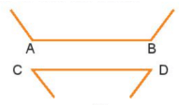
– Dùng thước đo kiểm tra được: AB = CD.
Hình c)

– Ước lượng bằng mắt bằng cách dóng thẳng điểm điểm A với điểm C, điểm B với điểm D (như hình vẽ). Dự đoán: AB = CD.

– Dùng thước đo kiểm tra được: AB = CD.
Bài 3 trang 93 sách bài tập Toán lớp 6 Tập 2: Điểm M nằm giữa hai điểm C và D. Tính độ dài đoạn thẳng CD, nếu:
a) CM = 2,5 cm và MD = 3,5 cm;
b) CM = 3,1 dm và MD = 4,6 dm;
c) CM = 12,3 m và MD = 5,8 m.
Lời giải:
Vì điểm M nằm giữa hai điểm C và D nên CD = CM + MD. Vì vậy ta có:
a) Thay CM = 2,5 cm và MD = 3,5 cm, ta được:
CD = CM + MD = 2,5 + 3,5 = 6 (cm);
Vậy CD = 6 cm.
b) Thay CM = 3,1 dm và MD = 4,6 dm, ta được:
CD = CM + MD = 3,1 + 4,6 = 7,7 (dm);
Vậy CD = 7,7 dm.
c) Thay CM = 12,3 m và MD = 5,8 m, ta được:
CD = CM + MD = 12,3 + 5,8 = 18,1 (m)
Vậy CD = 18,1 m.
Bài 4 trang 94 sách bài tập Toán lớp 6 Tập 2: Các điểm A, B, C nằm trên một đường thẳng. Biết rằng, AB = 4,3 cm, AC = 7,5 cm, BC = 3,2 cm. Trong ba điểm A, B, C điểm nào nằm giữa hai điểm còn lại?
Lời giải:
Ta có: AB + BC = 4,3 + 3,2 = 7,5 (cm).
Mà AC = 7,5 cm.
Nên: AB + BC = AC.
Vậy trong ba điểm A, B, C điểm B nằm giữa A và C.
Bài 5 trang 94 sách bài tập Toán lớp 6 Tập 2: Ba điểm A, B, C có cùng nằm trên một đường thẳng sao cho AB = 1,8 m, AC = 1,3 m, BC = 3m hay không? Hãy giải thích câu trả lời.
Lời giải:
Nếu AB + BC = AC thì điểm B nằm giữa A và C, đồng thời suy ra ba điểm này thẳng hàng.
Trong ba điểm A, B, C không có điểm nào nằm giữa hai điểm còn lại.
Vì giả sử điểm A nằm giữa hai điểm B và C, khi đó: AB + AC = BC.
Nhưng 1, 8 + 1,3 = 3,1 > 3 (m) hay AB + AC > BC nên vô lý.
Do đó điểm A không thể nằm giữa hai điểm B và C.
Tương tự: Vì 3 > 1,8 > 1,3 hay BC > AB > CA.
Nên: BC + CA > AB và BC + AB > AC.
Do đó điểm C không nằm giữa hai điểm A và B, đồng thời điểm B cũng không nằm giữa hai điểm A và C.
Vậy ba điểm A, B và C không cùng nằm trên một đường thẳng.
Bài 6 trang 94 sách bài tập Toán lớp 6 Tập 2: Trong hình vẽ bên các đoạn thẳng ME và NF bằng nhau. Hỏi các đoạn thẳng MF và NE có bằng nhau hay không? Vì sao?
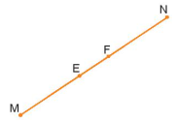
Lời giải:
Ta có: MF = ME + EF; NE = FN + EF.
Vì đoạn thẳng ME và NF bằng nhau hay ME = NF
Nên ME + EF = FN + EF.
Do đó MF = NE.
Vậy MF = NE.
Bài 7 trang 94 sách bài tập Toán lớp 6 Tập 2: Có hay không ba điểm A, B, C nằm trên một đường thẳng sao cho độ dài của đoạn thẳng AB bằng tổng độ dài của các đoạn thẳng AC và BC. Hãy vẽ hình trong trường hợp đó (nếu có).
Lời giải:
Đoạn thẳng AB bằng tổng độ dài các đoạn thẳng AC và BC.
Hay AC + BC = AB.
Do đó điểm C nằm giữa A và B, đồng thời ba điểm này thẳng hàng.
Ta có hình vẽ minh hoạ như sau:

Bài 8 trang 94 sách bài tập Toán lớp 6 Tập 2: Trên tia AB lấy điểm C. Tìm độ dài đoạn thẳng BC nếu:
a) AB = 1,5 m và AC = 0,3 m;
b) AB = 2 cm và AC = 4,4 cm.
Lời giải:
a) Trên tia AB, vì AB > AC (1,5 m > 0,3 m) nên điểm C nằm giữa A và B. Do đó: AC + BC = AB.
Suy ra BC = AB – AC = 1,5 – 0,3 = 1,2 (m).
Vậy BC = 1,2 m.
b) Trên tia AB, vì AB < AC (2 cm < 4,4 cm) nên điểm B nằm giữa A và C.
Do đó: AB + BC = AC.
Suy ra BC = AC – AB = 4,4 – 2 = 2,2 (cm).
Vậy BC = 2,2 cm.
Bài 9 trang 94 sách bài tập Toán lớp 6 Tập 2: Trên đoạn thẳng AB có độ dài 15 cm lấy một điểm C. Tìm độ dài của đoạn thẳng AC và BC nếu:
a) Đoạn thẳng AC ngắn hơn đoạn thẳng BC 3 cm;
b) Đoạn thẳng AC dài gấp hai lần đoạn thẳng BC;
c) Độ dài các đoạn thẳng AC và BC có tỉ lệ là 2 : 3.
Lời giải:
Vì điểm C nằm trên đoạn thẳng AB nên điểm C nằm giữa A và B.
Nên AC + BC = AB = 15 (cm).
a) Đoạn thẳng AC ngắn hơn đoạn thẳng BC 3 cm hay AC + 3 = BC.
Do đó AC + BC = AC + AC + 3 = 15
2AC = 15 – 3
2AC = 12
AC = 6 (cm)
Suy ra: BC = AC + 3 = 6 + 3 = 9 (cm).
Vậy AC = 6 cm, BC = 9 cm.
b) Đoạn thẳng AC dài gấp hai lần đoạn thẳng BC hay AC = 2BC.
Do đó AC + BC = 2BC + BC = 3BC = 15.
Suy ra BC = 15 : 3 = 5 (cm); AC = 2BC = 2 . 5 = 10 (cm).
Vậy BC = 5 cm, AC = 10 cm.
c) Độ dài các đoạn thẳng AC và BC có tỉ lệ là 2 : 3 hay AC : BC = 2 : 3.
Suy ra AC = 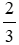 BC.
BC.
Do đó AC + BC = 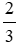 BC + BC = BC(
BC + BC = BC( 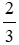 + 1) =
+ 1) = 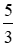 BC = 15.
BC = 15.
Suy ra BC = 15 : 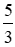 = 15.
= 15. 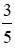 = 9 (cm); AC =
= 9 (cm); AC = 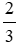 BC =
BC = 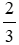 . 9 = 6 (cm).
. 9 = 6 (cm).
Vậy BC = 9 cm, AC = 6 cm.
Bài 10 trang 94 sách bài tập Toán lớp 6 Tập 2: Trên thang chia của thước bị mờ chỉ còn các điểm chia 0 cm; 5 cm và 13 cm. Có thể chỉ sử dụng chiếc thước này để vẽ các đoạn thẳng có độ dài lần lượt dưới đây hay không?
a) 3 cm;
b) 2 cm;
c) 1 cm.

Lời giải:
Dựa vào mối liên hệ giữa các số 5; 13 với lần lượt các số 1; 2; 3, ta có thể vẽ được các đoạn thẳng này.
a) Vì 3 cm = 13 cm – 5 cm – 5cm, nên ta có thể vẽ như sau:
+ Vẽ đoạn thẳng 13 cm.
+ Giữ thước trên đoạn thẳng đó, đánh dấu liên tiếp hai đoạn thẳng có độ dài 5 cm.
Đoạn thẳng còn lại sẽ dài 3 cm.
Ta có hình vẽ:
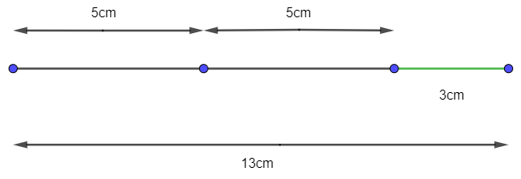
b) Vì 2 cm = 5 cm – 3 cm, ta có thể vẽ như sau:
+ Vẽ đoạn thẳng 5 cm.
+ Giữ thước trên đoạn thẳng đó, đánh dấu đoạn thẳng có độ dài 3 cm (dựa vào câu a).
Đoạn thẳng còn lại sẽ dài 2 cm.
Ta có hình vẽ:

c) Vì 1 cm = 3 cm – 2 cm, ta có thể vẽ như sau:
+ Vẽ đoạn thẳng 3 cm (dựa vào câu a).
+ Giữ thước trên đoạn thẳng đó, đánh dấu đoạn thẳng có độ dài 2 cm (dựa vào câu b).
Đoạn thẳng còn lại sẽ dài 1 cm.
Ta có hình vẽ:

Bài 11 trang 94 sách bài tập Toán lớp 6 Tập 2: Xác định khoảng cách giữa Thủ đô Hà Nội và Thành phố Hồ Chí Minh bằng bản đồ.
Hướng dẫn: Để tính khoảng cách trên thực tế giữa hai địa điểm bằng cách sử dụng bản đồ, ta đo khoảng cách giữa hai vị trí đó trên bản đồ rồi sử dụng tỉ lệ bản đồ. Chẳng hạn, nếu ta đo được khoảng cách giữa hai địa điểm ở trên bản đồ là 12 cm, tỉ lệ bản đồ là 1 : 1 000 000, thì khoảng cách trên thực tế của hai địa điểm đó là 12 000 000 cm hay 12 km.
Lời giải:
Chẳng hạn: Ta sử dụng bản đồ tỉ lệ 1 : 10 000 000, tức là 1 cm trên bản đồ tương ứng khoảng cách trên thực tế là 10 000 000 cm hay 100 km.

Ta đo được khoảng cách giữa Thủ đô Hà Nội và thành phố Hồ Chí Minh trên bản đồ xấp xỉ 8,5 cm.
Vậy khoảng cách thực tế giữa Thủ đô Hà Nội và thành phố Hồ Chí Minh xấp xỉ là: 8,5 . 100 = 850 (km).
====== ****&**** =====