Giải SBT Toán lớp 6 Bài 5: Trung điểm của đoạn thẳng
Bài 1 trang 96 sách bài tập Toán lớp 6 Tập 2: Những phát biểu nào sau đây là đúng?
a) Điểm I là trung điểm của đoạn thẳng MN thì IM = IN.
b) Khi IM = IN thì I là trung điểm của đoạn thẳng MN.
c) Để I là trung điểm của đoạn thẳng MN thì I thuộc đoạn thẳng MN và IM = IN.
Lời giải:
Trung điểm của đoạn thẳng là điểm nằm giữa hai đầu mút của đoạn thẳng (hay là điểm đó thuộc đoạn thẳng cho trước) và cách đều hai đầu mút đó.
Do đó, phát biểu c) đúng.
Trung điểm của đoạn thẳng còn được gọi là điểm chính giữa của đoạn thẳng đó.
Do đó, phát biểu a) đúng.
Phát biểu b) sai vì, chẳng hạn: IM = IN = 5cm nhưng I không thuộc đoạn thẳng MN (như hình vẽ), thì I không phải là trung điểm của MN.
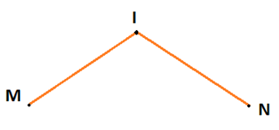
Vậy phát biểu a), c) là đúng.
Bài 2 trang 96 sách bài tập Toán lớp 6 Tập 2: Cho đoạn thẳng MN có trung điểm K. Gọi E là trung điểm của đoạn thẳng KN. Biết EN = 5cm, em hãy tính độ dài các đoạn thẳng MK, ME và MN.
Lời giải:
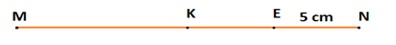
Vì E là trung điểm của đoạn thẳng KN nên E nằm giữa hai điểm K, N và KE = EN = 5cm.
Do đó: KN = KE + EN = 5 + 5 = 10 (cm).
Vì K là trung điểm của đoạn thẳng MN nên K nằm giữa hai điểm M, N và MK = KN = 10 cm.
Do đó: MN = MK + KN = 10 + 10 = 20 (cm).
Vì K nằm giữa hai điểm M và E nên:
ME = MK + KE = 10 + 5 = 15 (cm).
Vậy MK = 10 cm, ME = 15 cm và MN= 20 cm.
Bài 3 trang 96 sách bài tập Toán lớp 6 Tập 2: Trên tia Ox lấy hai điểm M và N sao cho OM = 3 cm, ON = 6 cm.
a) Trong ba điểm O, M, N điểm nào nằm giữa hai điểm còn lại?
b) Điểm M có là trung điểm của đoạn thẳng ON hay không? Vì sao?
c) Lấy K là trung điểm của OM, H là trung điểm của MN. M có là trung điểm của KH không? Hãy giải thích.
Lời giải:

a) Trên tia Ox, ta có: OM = 3cm < ON = 6 cm.
Do đó điểm M nằm giữa điểm O và điểm N.
b) Vì điểm M nằm giữa hai điểm O và N nên:
OM + MN = ON hay 3 + MN = 6.
Suy ra MN = 6 – 3 = 3 (cm).
Mà OM = 3 cm nên OM = MN = 3cm.
Vậy điểm M là trung điểm của đoạn thẳng ON vì:
+) Điểm M nằm giữa điểm O và điểm N.
+) OM = MN = 3cm.
c) Vì K là trung điểm của OM nên K nằm giữa O và M và OK = KM = OM : 2 = 3 : 2 = 1,5 cm.
Vì H là trung điểm của MN nên H nằm giữa M và N và MH = HN = MN : 2 = 3 : 2 = 1,5 cm.
Do đó: KM = MH = 1,5 cm.
Vì K nằm giữa O và M, H nằm giữa M và N nên M nằm giữa K và H.
Vậy M là trung điểm của KH.
Bài 4 trang 96 sách bài tập Toán lớp 6 Tập 2: Cho ba điểm O, A, B thẳng hàng sao cho điểm O nằm giữa A và B, OA = 10 cm, OB = 6 cm. Gọi M, N lần lượt là trung điểm của OA và OB. Tính độ dài đoạn thẳng MN.
Lời giải:

Vì M là trung điểm OA và OA = 10 cm nên:
MO = MA = 10 : 2 = 5 (cm).
Vì N là trung điểm OB và OB = 6 cm nên:
NO = NB = 6 : 2 = 3 (cm)
Mặt khác, O nằm giữa A và B, M nằm giữa A và O, N nằm giữa O và B nên O nằm giữa M và N.
Vậy MN = MO + ON = 5 + 3 = 8 (cm).
Bài 5 trang 96 sách bài tập Toán lớp 6 Tập 2: Trên tia Ox lấy hai điểm P và Q sao cho OP = 4 cm, OQ = 8 cm. I là trung điểm của đoạn PQ. Tính OI.
Lời giải:

Trên tia Ox, ta có: OP < OQ (4 cm < 8 cm).
Do đó, P nằm giữa hai điểm O và Q.
Vì I là trung điểm của đoạn PQ nên I nằm giữa P và Q.
Do P nằm giữa O và Q, I nằm giữa P và Q.
Suy ra P nằm giữa O và I.
Do đó OI = OP + IP.
Vì P nằm giữa O và Q nên OQ = OP + PQ
Suy ra: PQ = OQ – OP = 8 – 4 = 4 (cm).
Vì I là trung điểm PQ nên:
IP = IQ = PQ : 2 = 4 : 2 = 2 (cm)
Vì P nằm giữa O và I nên:
OI = PO + IP = 4 + 2 = 6 (cm).
Vậy OI = 6 cm.
Bài 6 trang 96 sách bài tập Toán lớp 6 Tập 2: Cho đoạn thẳng OA = 5 cm. Hãy vẽ điểm B sao cho:
a) A là trung điểm của đoạn OB.
b) O là trung điểm của của đoạn AB.
Lời giải:
a) Vì A là trung điểm của OB nên:
+) Điểm A nằm giữa hai điểm O và B.
+) OA = AB = 5cm.
Vậy trên tia OA, ta lấy điểm B sao cho AB = 5 cm và A nằm giữa O và B.
Ta có hình minh họa:

b) Vì O là trung điểm AB nên:
+) Điểm O nằm giữa hai điểm A và B.
+) OA = OB = 5cm.
Vậy trên đường thẳng OA, ta lấy điểm B sao cho OB = 5 cm và O nằm giữa A và B.
Ta có hình minh họa:

Bài 7 trang 96 sách bài tập Toán lớp 6 Tập 2: Cho hai đoạn thẳng AB và CD có cùng trung điểm M như hình vẽ. Biết AB = 12 cm, CD = 6 cm. Hãy tính độ dài của hai đoạn thẳng AM và AD.

Lời giải:

Vì M là trung điểm AB nên:
AM = MB = AB : 2 = 12 : 2 = 6 (cm).
Vì M là trung điểm CD nên:
CM = MD = CD : 2 = 6 : 2 = 3 (cm).
Dễ thấy: M nằm giữa hai điểm A và D nên:
AD = AM + MD = 6 + 3 = 9 (cm).
Vậy AM = 6 cm, AD = 9 cm.
Bài 8 trang 96 sách bài tập Toán lớp 6 Tập 2: Em hãy vẽ đoạn thẳng AB và dự đoán trung điểm của đoạn thẳng đó. Sau hãy dùng thước kiểm tra lại dự đoán đó.
Lời giải:
Chẳng hạn: Vẽ đoạn thẳng AB.

Dự đoán trung điểm I:
Vì I là trung điểm của đoạn thẳng AB nên IA = IB = 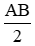 .
.
Ước lượng vị trí điểm I sao cho IA = IB =  .
.
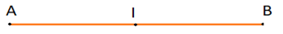
Kiểm tra: dùng thước kẻ, ta đo được độ dài AB = 10 cm.
Vậy I là trung điểm nếu IA = IB = 5cm. Ta sửa lại:
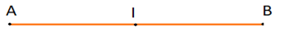
Bài 9 trang 96 sách bài tập Toán lớp 6 Tập 2: Cho một đoạn dây, em có những cách nào để tìm ra trung điểm của đoạn dây đó?
Lời giải:
Cách 1: Ta có thể gấp đôi đoạn dây đó lại, sao cho hai đầu dây trùng nhau, điểm gấp chính là trung điểm của đoạn dây.
Cách 2: Ta có thể dùng thước để đo độ dài đoạn dây, sau đó tính một nửa độ dài của đoạn dây đó.
Dùng thước để xác định vị trí mà độ dài từ một đầu đoạn dây tới đó bằng một nửa độ dài đoạn dây đã cho, ta sẽ tìm được trung điểm của đoạn dây.
====== ****&**** =====