Sách bài tập Toán 7 Bài 14 (Kết nối tri thức): Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Giải SBT Toán lớp 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Giải trang 60 Tập 1

Bài 4.21 trang 60 Tập 1: Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.

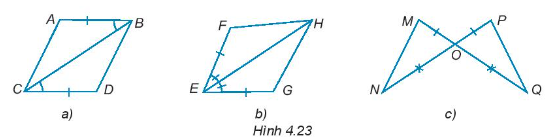
Sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức (ảnh 1)

Hướng dẫn giải

*) Hình a:

Xét ∆ABC và ∆DCB có:

AB = CD (giả thiết)

BC chung

$\hat{A B C} = \hat{D C B}$ (giả thiết)

Do đó, ∆ABC = ∆DCB (c – g – c).

*) Hình b:

Xét ∆EFH và ∆EGH có:

EF = EG (giả thiết)

EH chung

$\hat{F E H} = \hat{G E H}$ (giả thiết)

Do đó, ∆EFH = ∆EGH (c – g – c)

*) Hình c:

Xét ∆MON và ∆POQ có:

MO = PO (giả thiết)

NO = QO (giả thiết)

$\hat{M O N} = \hat{P O Q}$ (hai góc đối đỉnh)

Do đó, ∆MON = ∆POQ (c – g – c).

Giải trang 61 Tập 1

Bài 4.22 trang 61 Tập 1: Cho hai tam giác ABC và DEF bất kỳ, thỏa mãn AB = FE, BC = DF, $\hat{A B C} = \hat{D F E}$ . Những câu nào dưới đây đúng?

a) ∆ABC = ∆DFE.

b) ∆BAC = ∆EFD.

c) ∆CAB = ∆EFD.

d) ∆ABC = ∆EFD.

Hướng dẫn giải

Vì $\hat{A B C} = \hat{D F E}$ nên đỉnh B tương ứng với đỉnh F;

Vì AB = FE mà đỉnh B ứng với đỉnh F thì đỉnh A ứng với đỉnh E.

Suy ra đỉnh C ứng với đỉnh D.

Xét tam giác ABC và tam giác EFD có:

AB = FE;

BC = DF;

$\hat{A B C} = \hat{D F E}$ .

Do đó, ∆ABC = ∆EFD (c – g – c).

Vậy chỉ có đáp án d) đúng.

Bài 4.23 trang 61 Tập 1: Cho hai tam giác ABC và MNP bất kì, thỏa mãn $\hat{A B C} = \hat{P N M}$ , $\hat{A C B} = \hat{N P M}$ và BC = PN. Những câu nào dưới đây đúng?

a) ∆ABC = ∆PNM.

b) ∆ABC = ∆NPM.

c) ∆ABC = ∆MPN.

d) ∆ABC = ∆MNP.

Hướng dẫn giải

Vì $\hat{A B C} = \hat{P N M}$ nên đỉnh B tương ứng với đỉnh N;

Vì $\hat{A C B} = \hat{N P M}$ nên đỉnh C tương ứng với đỉnh P.

Suy ra đỉnh A tương ứng với đỉnh M.

Xét tam giác ABC và tam giác MNP có:

$\hat{A B C} = \hat{P N M}$

$\hat{A C B} = \hat{N P M}$

BC = PN

Do đó, ∆ABC = ∆MNP (g – c – g).

Trong bốn đáp án chỉ có đáp án d chính xác.

Bài 4.24 trang 61 Tập 1:Cho các điểm A, B, C, D như Hình 4.24, biết rằng AC = BD và $\hat{D B A} = \hat{C A B}$ .

Chứng minh rằng AD = BC.

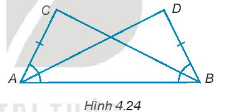
Sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức (ảnh 1)

Hướng dẫn giải

Xét ∆ABC và ∆BAD có:

AC = BD (giả thiết)

AB chung

$\hat{C A B} = \hat{D B A}$ (giả thiết)

Do đó, ∆ABC = ∆BAD (c – g – c)

Suy ra, BC = AD (hai cạnh tương ứng).

Bài 4.25 trang 61 Tập 1: Cho các điểm A, B, C, D như Hình 4.25, biết rằng $\hat{B A C} = \hat{B A D}$ và $\hat{B C A} = \hat{B D A}$ .

Chứng minh rằng ∆ABC = ∆ABD.

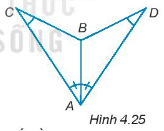
Sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức (ảnh 1)

Hướng dẫn giải

Xét tam giác ABC có:

$\hat{A B C} + \hat{B A C} + \hat{B C A} = 180 °$

$\hat{A B C} = 180 ° - \hat{B A C} - \hat{B C A}$ (1)

Xét tam giác ABD có:

$\hat{A B D} + \hat{B A D} + \hat{B D A} = 180 °$

$\hat{A B D} = 180 ° - \hat{B A D} - \hat{B D A}$ (2)

Mà $\hat{B A C} = \hat{B A D}$ ; $\hat{B C A} = \hat{B D A}$ (3)

Từ (1), (2), (3) ta suy ra $\hat{A B C} = \hat{A B D}$ .

Xét ∆ABC và ∆ABD có:

$\hat{A B C} = \hat{A B D}$ (chứng minh trên)

AB chung

$\hat{B A C} = \hat{B A D}$ (giả thiết)

Do đó, ∆ABC = ∆ABD (g – c – g).

Bài 4.26 trang 61 Tập 1: Cho các điểm A, B, C, D, E như Hình 4.26, biết rằng AB = CD, $\hat{B A E} = \hat{D C E}$ . Chứng minh rằng:

a) E là trung điểm của các đoạn thẳng AC và BD.

b) ∆ACD = ∆CAB.

c) AD song song với BC.

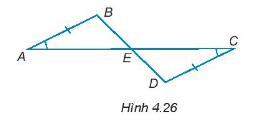
Sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức (ảnh 1)

Hướng dẫn giải

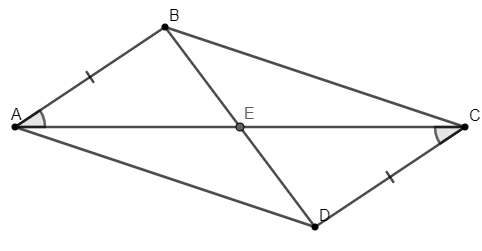
Sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức (ảnh 1)

a) Xét tam giác ABE có:

$\hat{B A E} + \hat{A B E} + \hat{A E B} = 180 °$

$\hat{A B E} = 180 ° - \hat{B A E} - \hat{A E B}$ (1)

Xét tam giác CDE có:

$\hat{D C E} + \hat{D E C} + \hat{E D C} = 180 °$

$\hat{E D C} = 180 ° - \hat{D C E} - \hat{D E C}$ (2)

Mà $\hat{B A E} = \hat{D C E}$ (giả thiết); $\hat{A E B} = \hat{D E C}$ (hai góc đối đỉnh) (3)

Từ (1), (2), (3) ta suy ra $\hat{A B E} = \hat{E D C}$ .

Xét ∆ABE và ∆CDE có:

$\hat{A B E} = \hat{E D C}$ (chứng minh trên)

AB = CD (giả thiết)

$\hat{B A E} = \hat{D C E}$ (giả thiết)

Do đó, ∆ABE = ∆CDE (g – c – g).

Suy ra, AE = CE; BE = DE (các cặp cạnh tương ứng)

Vì AE = CE và E nằm giữa A và C nên E là trung điểm của AC;

Vì BE = DE và B nằm giữa D và B nên E là trung điểm của BD.

b) Xét ∆ACD và ∆CAB có:

CD = AB (giả thiết)

AC chung

$\hat{B A C} = \hat{D C A}$ (giả thiết)

Do đó, ∆ACD = ∆CAB (c – g – c).

c) Vì ∆ACD = ∆CAB nên $\hat{D A C} = \hat{B C A}$ (hai góc tương ứng)

Mà hai góc này ở vị trí so le trong nên AD song song với BC.

Giải trang 62 Tập 1

Bài 4.27 trang 62 Tập 1: Cho các điểm A, B, C, D, E như Hình 4.27, biết rằng AD = BC, $\hat{A D E} = \hat{B C E}$ . Chứng minh rằng:

a) $\hat{D A C} = \hat{C B D}$ .

b) ∆AED = ∆BEC.

c) AB song song với DC.

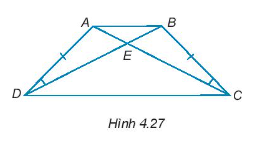
Sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức (ảnh 1)

Hướng dẫn giải

a) Xét tam giác AED có:

$\hat{A D E} + \hat{D A E} + \hat{A E D} = 180 °$

$\hat{D A E} = 180 ° - \hat{A D E} - \hat{A E D}$ (1)

Xét tam giác BEC có:

$\hat{B C E} + \hat{E B C} + \hat{B E C} = 180 °$

$\hat{E B C} = 180 ° - \hat{B C E} - \hat{B E C}$ (2)

Mà $\hat{A D E} = \hat{B C E}$ ; $\hat{A E D} = \hat{B E C}$ (hai góc đối đỉnh) (3)

Từ (1); (2); (3) suy ra, $\hat{D A E} = \hat{E B C}$ hay $\hat{D A C} = \hat{C B D}$ (điều phải chứng minh).

b) Xét ∆AED và ∆BEC ta có:

$\hat{D A E} = \hat{E B C}$ (chứng minh trên)

$\hat{A D E} = \hat{B C E}$ (giả thiết)

AD = CB (giả thiết)

Do đó, ∆AED = ∆BEC (g – c – g).

c) Vì ∆AED = ∆BEC nên AE = BE; ED = EC.

Ta có: AC = AE + EC; BD = BE + ED.

Do đó, AC = BD.

Xét ∆ABD và ∆BAC ta có:

AC = BD (chứng minh trên)

AB chung

AD = CB (giả thiết)

Do đó, ∆ABD = ∆BAC (c – c – c)

Suy ra $\hat{A B D} = \hat{B A C}$ (hai góc tương ứng)

Xét tam giác AEB có:

$\hat{A B E} + \hat{B A E} + \hat{A E B} = 180 °$

Do đó, $2 \hat{A B E} = 180 ° - \hat{A E B}$ (vì $\hat{A B E} = \hat{B A E}$ do $\hat{A B D} = \hat{B A C}$ )

Suy ra $\hat{A B E} = \frac{180 ° - \hat{A E B}}{2}$ (4)

Xét ∆ACD và ∆BDC ta có:

AC = BD (chứng minh trên)

CD chung

AD = CB (giả thiết)

Do đó, ∆ACD = ∆BDC (c – c – c)

Suy ra $\hat{A C D} = \hat{B D C}$ (hai góc tương ứng)

Xét tam giác DEC có:

$\hat{D C E} + \hat{E D C} + \hat{D E C} = 180 °$

Do đó, $2 \hat{E D C} = 180 ° - \hat{D E C}$ (vì $\hat{E D C} = \hat{D C E}$ do $\hat{A C D} = \hat{B D C}$ )

Suy ra $\hat{E D C} = \frac{180 ° - \hat{D E C}}{2}$ (5)

Lại có, $\hat{A E B}, \hat{D E C}$ là hai góc đối đỉnh nên $\hat{A E B} = \hat{D E C}$ (6)

Từ (4); (5); (6) suy ra $\hat{A B E}$ = $\hat{E D C}$ hay $\hat{A B D} = \hat{B D C}$ .

Mà hai góc này lại ở vị trí so le trong nên AB // CD.

Bài 4.28 trang 62 Tập 1: Cho tam giác ABC bằng tam giác DEF (H.4.28).

a) Gọi M và N lần lượt là trung điểm các đoạn thẳng BC và EF. Chứng minh rằng AM = DN.

b) Trên hai cạnh AC và DF lấy hai điểm P và Q sao cho BP, EQ lần lượt là phân giác của các góc $\hat{A B C}$ và $\hat{D E F}$ . Chứng minh rằng: BP = EQ.

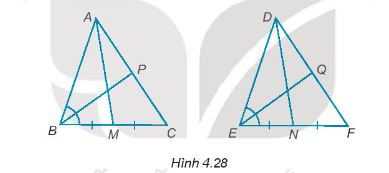
Sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức (ảnh 1)

Hướng dẫn giải

a) Vì ∆ABC = ∆DEF nên

$\{\begin{cases} \hat{A B C} = \hat{D E F}; \hat{B A C} = \hat{E D F}; \\ \hat{A C B} = \hat{D F E} \\ A B = D E; B C = E F; A C = D F \end{cases}$

Vì M là trung điểm của BC nên BM = MC = $\frac{1}{2} B C$ .

Vì N là trung điểm của EF nên EN = NF = $\frac{1}{2} E F$ .

Mà BC = EF (chứng minh trên) nên BM = EN.

Xét ∆ABM và ∆DEN ta có:

BM = EN (chứng minh trên)

AB = DE (chứng minh trên)

$\hat{A B M} = \hat{D E N}$ (do $\hat{A B C} = \hat{D E F}$ chứng minh trên)

Do đó, ∆ABM = ∆DEN (c – g – c).

Suy ra, AM = DN (hai cạnh tương ứng).

b) Vì BP là tia phân giác của góc $\hat{A B P}$ nên $\hat{A B P} = \hat{P B C} = \frac{\hat{A B C}}{2}$

Vì EQ là tia phân giác của góc $\hat{D E F}$ nên $\hat{D E Q} = \hat{Q E F} = \frac{\hat{D E F}}{2}$

Mà $\hat{A B C}$ = $\hat{D E F}$ nên $\hat{P B C}$ = $\hat{Q E F}$ .

Xét ∆PBC và ∆QEF ta có:

BC = EF (chứng minh trên)

$\hat{P B C}$ = $\hat{Q E F}$ (chứng minh trên)

$\hat{P C B} = \hat{Q F E}$ (do $\hat{A C B} = \hat{D F E}$ chứng minh trên)

Do đó, ∆PBC = ∆QEF (g – c – g)

Suy ra, BP = EQ (hai cạnh tương ứng).

Bài 4.29 trang 62 Tập 1: Gọi M và N lần lượt là trung điểm các đoạn thẳng cạnh BC và EF của hai tam giác ABC và DEF. Giả sử rằng AB = DE, BC = EF, AM = DN (H.4.29). Chứng minh rằng ∆ABC = ∆DEF.

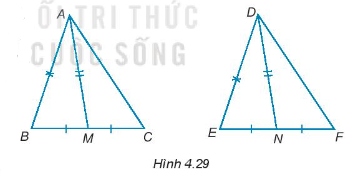
Sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức (ảnh 1)

Hướng dẫn giải

Vì M là trung điểm của BC nên BM = MC = $\frac{B C}{2}$

Vì N là trung điểm của EF nên EN = NF = $\frac{E F}{2}$

Mà BC = EF (giả thiết) nên BM = EN.

Xét ∆ABM và ∆DEN ta có:

AB = DE (giả thiết)

BM = EN (chứng minh trên)

AM = DN (giả thiết)

Do đó, ∆ABM = ∆DEN (c – c – c).

Suy ra, $\hat{A B M} = \hat{D E N}$ (hai góc tương ứng) hay $\hat{A B C} = \hat{D E F}$ .

Xét ∆ABC và ∆DEF ta có:

AB = DE (giả thiết)

BC = EF (giả thiết)

$\hat{A B C} = \hat{D E F}$ (chứng minh trên)

Do đó, ∆ABC = ∆DEF (c – g – c).

Bài 4.30 trang 62 Tập 1:Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OB = OC = OD như Hình 4.30. Chứng minh ABCD là hình chữ nhật.

Sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức (ảnh 1)

Hướng dẫn giải

Xét ∆OAB và ∆OCD ta có:

OA = OC (giả thiết)

$\hat{A O B} = \hat{C O D}$ (hai góc đối đỉnh)

OB = OD (giả thiết)

Do đó, ∆OAB = ∆OCD (c – g – c).

Suy ra AB = DC và $\hat{B A O} = \hat{O C D}$ hay $\hat{B A C} = \hat{A C D}$ .

Mà hai góc này ở vị trí so le trong, do đó AB // DC (1).

Xét ∆OAD và ∆OCB ta có:

OA = OC (giả thiết)

$\hat{A O D} = \hat{B O C}$ (hai góc đối đỉnh)

OD = OB (giả thiết)

Do đó, ∆OAD = ∆OCB (c – g – c).

Suy ra AD = BC và $\hat{O A D} = \hat{O C B}$ hay $\hat{C A D} = \hat{A C B}$ .

Mà hai góc này ở vị trí so le trong nên AD // BC (2).

Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành.

Ta có: OA = OC = OB = OD, AC = OA + OC, BD = OB + OD.

Do đó, AC = BD.

Xét tam giác ABD và tam giác DCA có:

AB = DC (chứng minh trên)

AD: cạnh chung

BD = AC (chứng minh trên)

Do đó, ∆ABD = ∆DCA (c – c – c).

Suy ra $\hat{B A D} = \hat{C D A}$ .

Lại có: $\hat{B A D} + \hat{C D A} = 180 °$ (do AB // DC, hai góc ở vị trí trong cùng phía)

Do đó: $\hat{B A D} = \hat{C D A} = \frac{180 °}{2} = 90 °$ .

Vậy hình bình hành ABCD có một góc vuông nên nó là hình chữ nhật.

Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Bài 15: Các trường hợp bằng nhau của tam giác vuông

Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng

Ôn tập chương 4

====== ****&**** =====

Bài liên quan:

Leave a Comment Hủy