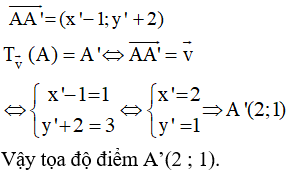Bài tập Toán 11 Chương 1 Bài 1-2: Phép biến hình. Phép tịnh tiến
A. Bài tập Phép biến hình- Phép tịnh tiến
I. Bài tập trắc nghiệm
Bài 1: Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto (1;1) biến điểm A(0;2) thành A’ và biến điểm B(-2;1) thành B’, khi đó:
A. A’B’ =
B. A’B’ =
C. A’B’ =
D. A’B’ =
Lời giải:
Đáp án: A
Phép tịnh tiến theo vecto (1;1) biến A(0; 2) thành A’(1; 3) và biến B(-2; 1) thành B’(-1; 2) ⇒ A’B’ =
Bài 2: Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto (1;0) biến đường thẳng d: x – 1 = 0 thành đường thẳng d’ có phương trình:
A. x – 1 = 0
B. x – 2 = 0
C. x – y – 2 = 0
D. y – 2 = 0
Lời giải:
Đáp án: B
Lấy M(x; y) thuộc d; gọi M’(x’; y’) là ảnh của M qua phép tịnh tiến theo vecto (1;0) thì
Thay vào phương trình d ta được x’ – 2 = 0, hay phương trình d’ là x – 2 = 0 .
Bài 3: Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto (3;1) biến đường thẳng d: 12x – 36y + 101 = 0 thành đường thẳng d’ có phương trình:
A. 12x – 36y – 101 = 0
B. 12x + 36y + 101 = 0
C.12x + 36y – 101 = 0
D. 12x – 36y + 101 = 0.
Lời giải:
Đáp án: D
Vecto chỉ phương của d có tọa độ (3; 1) cùng phương với vecto nên phép tịnh tiến theo vecto (3;1) biến đường thẳng d thành chính nó.
Bình luận: Nếu không tinh ý nhận ra điều trên, cứ làm bình thường theo quy trình thì sẽ rất lãng phí thời gian.
Bài 4: Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto (-2;-1) biến thành parabol (P): y = x2 thành parabol (P’) có phương trình:
A. y = x2 + 4x – 5
B. y = x2 + 4x + 4
C. y = x2 + 4x + 3
D. y = x2 – 4x + 5
Lời giải:
Đáp án: C
Lấy M(x; y) thuộc (P); gọi M’(x’; y’) là ảnh của M qua phép tịnh tiến theo vecto (-2; -1) thì:
thay vào phương trình (P) được y’ + 1 = (x’+ 2)2 ⇒ y’ = x’2 + 4x’ + 3 hay y = x2 + 4x + 3.
Bài 5: Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto (-3;-2) biến đường tròn có phương trình (C): x2 + (y – 1)2 = 1 thành đường tròn (C’) có phương trình:
A. (x – 3)2 + (y + 1)2 = 1
B. (x + 3)2 + (y + 1)2 = 1
C. (x + 3)2 + (y + 1)2 = 4
D. (x – 3)2 + (y – 1)2 = 4
Lời giải:
Đáp án: B
Đường tròn (C) có tâm I(0; 1) và bán kính R = 1.
Phép tịnh tiến theo vecto (-3; -2) biến tâm I(0; 1) của (C) thành tâm I’ của (C’) có cùng bán kính R’ = R = 1
Ta có
⇒ phương trình (C’) là (x + 3)2 + (y + 1)2 = 1.
Chú ý: Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính.
Bài 6: Phép biến hình biến điểm M thành điểm M’ thì với mỗi điểm M có:
A. Ít nhất một điểm M’ tương ứng
B. Không quá một điểm M’ tương ứng
C. Vô số điểm M’ tương ứng
D. Duy nhất một điểm M’ tương ứng
Lời giải:
Đáp án: D
Hướng dẫn giải: quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M’ của mặt phẳng đó gọi là phép biến hình trong mặt phẳng.
Bài 7: Cho tam giác ABC nội tiếp đường trong (O). Qua O kẻ đường thẳng d. Quy tắc nào sau đây là một phép biến hình.
A. Quy tắc biến O thành giao điểm của d với các cạnh tam giác ABC
B. Quy tắc biến O thành giao điểm của d với đường tròn O
C. Quy tắc biến O thành hình chiếu của O trên các cạnh của tam giác ABC
D. Quy tắc biến O thành trực tâm H, biến H thành O và các điểm khác H và O thành chính nó.
Lời giải:
Đáp án: D
Các quy tắc A, B, C đều biến O thành nhiều hơn một điểm nên đó không phải là phép biến hình. Quy tắc D biến O thành điểm H duy nhất nên đó là phép biến hình. Chọn đáp án D
Bài 8: Cho hình vuông ABCD có M là trung điểm của BC. Phép tịnh tiến theo vecto biến M thành A thì bằng:
Lời giải:
Đáp án: C
Bài 9: Cho tam giác ABC có trực tâm H, nội tiếp đường tròn (O), BC cố định, I là trung điểm của BC. Khi A di động trên (O) thì quỹ tích H là đường tròn (O’) là ảnh của O qua phép tịnh tiến theo vecto bằng:
A.
B.
C. 2
D.
Lời giải:
Đáp án: C
Gọi A’ là điểm đối xứng với A qua O. Ta có: BH // A’C suy ra BHCA’ là hình bình hành do đó HA’ cắt BC tại trung điểm I của BC. Mà O là trung điểm của AA’ suy ra OI là đường trung bình của tam giác AHA’ suy ra = 2
Cách 2: Gọi B’ là điểm đối xứng với B qua O, chứng minh AHCB’ là hình bình hành rồi suy ra
Bài 10: Mặt phẳng tọa độ, phép tịnh tiến theo vecto (2; -3) biến đường thẳng d: 2x + 3y – 1 = 0 thành đường thẳng d’ có phương trình
A. 3x + 2y – 1 = 0
B. 2x + 3y + 4 = 0
C. 3x + 2y + 1 = 0
D. 2x + 3y + 1 = 0
Lời giải:
Đáp án: B
Phép tịnh tiến theo vecto (2; -3) biến điểm M (x; y) thành điểm M’(x’; y’) thì:
hay vào phương trình d được:
2(x’ – 2) + 3(y’ + 3) – 1 = 0 ⇒ 2x’ + 3y’ + 4 = 0
hay 2x + 3y + 4 = 0.
II. Bài tập tự luận có lời giải
Bài 1: Tìm mệnh đề đúng trong các mệnh đề sau:
A. phép tịnh tiến theo vecto biến M thành M’ thì =
B. Phép tịnh tiến là phép đồng nhất khi vecto tịnh tiến là
C. Phép tịnh tiến theo vecto biến M thành M’ và N thành N’ thì tứ giác MNM’N’ là hình bình hành
D. Phép tịnh tiến theo vecto biến đường tròn (O;R) thành đường tròn (O;R)
Lời giải:
Đáp án: B
Phương án A. = mới đúng nghĩa. Phương án C. Tứ giác MNN’M’ mới là hình bình hành. Phương án D. phép tịnh tiến theo vecto chi biến đường tròn (O; R) thành đường tròn (O; R) khi vecto tịnh tiến bằng vecto không.
Bài 2: Cho tam giác ABC có trọng tâm G, Gọi D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB. Mệnh đề nào sau đây là sai.
A. T (F) = E
B . (B) = F
C. T2DG→ (A) = G
D. T GA→(D) = G
Lời giải:
Đáp án: C
Bài 3: Trong mặt phẳng tọa độ, phép tịnh tiến theo (1;2) biến điểm M (-1; 4) thành điểm M’ có tọa độ là?
Lời giải:
Thay vào công thức:
Bài 4: Trong mặt phẳng tọa độ cho điểm M(-10;1) và điểm M’(3;8). Phép tịnh tiến theo vecto biến M thành M’, thì tọa độ vecto là:
Lời giải:
Ta có: x’- x = 13; y’- y = 7
Bài 5: Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto (0;0) biến điểm A(0;2) thành điểm A’ có tọa độ:
Lời giải:
Đáp án: D
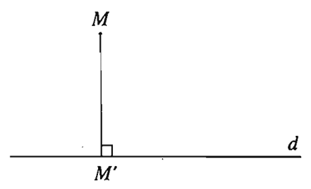
Bài 6: Trong mặt phẳng cho đường thẳng d và M. Dựng hình chiếu vuông góc M’ của điểm M lên đường thẳng d.
Lời giải:
Từ M kẻ đường thẳng vuông góc với d cắt d tại M’
⇒ M’là hình chiếu của M trên đường thẳng d
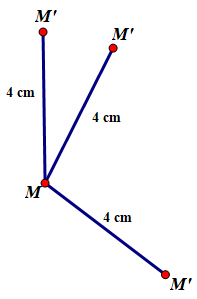
Bài 7 Cho trước số a dương, với mỗi điểm M trong mặt phẳng, gọi M’ là điểm sao cho MM’ = a. Quy tắc đặt tương ứng điểm M với điểm M’ nêu trên có phải là một phép biến hình không?
Lời giải:
Quy tắc đặt tương ứng điểm M với điểm M’ nêu trên không phải là một phép biến hình vì M’ không phải là điểm duy nhất được xác định trên mặt phẳng
Ví dụ minh họa: a = 4 cm
Bài 8 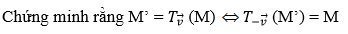
Lời giải:
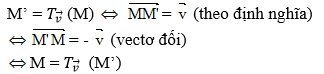
Bài 9 Cho tam giác ABC có G là trọng tâm. Dựng ảnh của tam giác ABC qua phép tịnh tiến theo vectơ AG . Dựng điểm D sao cho phép tịnh tiến theo vectơ AG biến D thành A.
Lời giải:
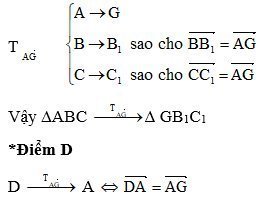
<=> A là trung điểm của đoạn thẳng DG
Bài 10 Trong mặt phẳng tọa độ Oxy cho vectơ = (-1; 2), A(3; 5), B(-1; 1) và đường thẳng d có phương trình x – 2y + 3 = 0.
a. Tìm tọa độ của các điểm A’, B’ theo thứ tự là ảnh của A, B qua phép tịnh tiến theo vecto v.
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ .
c. Tìm phương trình của đường thẳng d’ là ảnh của d qua phép tịnh tiến theo v.
Lời giải:
a. Gọi tọa độ của A’ là (x’, y’). Theo công thức tọa độ của phép tịnh tiến, ta có:
vecto v = (-1; 2), A(3; 5); A’ = Tv.(A) => x’ = – 1 + 3 => x’ = 2
y’ = 2 + 5 => y’ = 7 => A’(2, 7)
Tương tự, ta tính được B’(-2 ; 3).
b. Gọi tọa độ của C là (x; y). A(3; 5) là ảnh của C qua phép tịnh tiến theo vectơ
c. Vì d’ = Tv.(d) nên d’ // d, do đó để viết phương trình của d’, ta tìm một điểm M ∈ d và ảnh M’ của nó qua phép tịnh tiến theo vectơ và sau đó viết phương trình đường thẳng đi qua M’ và song song với d.
Trong phương trình x – 2y + 3 = 0, cho y = 0 thì x = – 3. Vậy ta được điểm M(-3; 0) thuộc d.
Đường thẳng d có phương trình: x – 2y + 3 = 0
Đường thẳng d’ song song với d có phương trình x – 2y + m =0, d’ đi qua M’ nên:
(-4) – 2.2 + m = 0 <=> m = 8.
Vậy phương trình của d’ là: x – 2y + 8 = 0
III. Bài tập vận dụng
Bài 1 Cho hai đường thẳng a và b song song với nhau. Hãy chỉ ra một phép tịnh tiến biến a thành b. Có bao nhiêu phép tịnh tiến như thế?
Bài 2 Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto(1;0) biến đường thẳng d: x – 1 = 0 thành đường thẳng d’ có phương trình?
Bài 3 Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto (3;1) biến đường thẳng d: 12x – 36y + 101 = 0 thành đường thẳng d’ có phương trình?
Bài 4 Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto (-3;-2) biến đường tròn có phương trình (C): x2 + (y – 1)2 = 1 thành đường tròn (C’) có phương trình?
Bài 5 Cho tam giác ABC nội tiếp đường trong (O). Qua O kẻ đường thẳng d. Quy tắc nào là một phép biến hình?
Bài 6 Cho tam giác ABC có G là trọng tâm. Xác định ảnh của tam giác ABC qua phép tịnh tiến theo vectơ AG biến D thành A .
Bài 7 Cho hai đường thẳng a và b song song với nhau. Hãy chỉ ra một phép tịnh tiến biến a thành b. Có bao nhiêu phép tịnh tiến như thế?
Bài 8 Cho hình vuông ABCD có M là trung điểm của BC. Phép tịnh tiến theo vecto biến M thành A thì bằng?
Bài 9 Mặt phẳng tọa độ, phép tịnh tiến theo vecto (2; -3) biến đường thẳng d: 2x + 3y – 1 = 0 thành đường thẳng d’ có phương trình
Bài 10 Cho tam giác ABC có trọng tâm G, Gọi D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB. Mệnh đề nào sau đây là sai.
B. Lý thuyết Phép biến hình
1. Định nghĩa.
– Quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M’ của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng.
– Nếu kí hiệu phép biến hình là F thì ta viết F(M) = M’ hay M’ = F(M) và gọi M’ là ảnh của điểm M qua phép biến hình F.
– Nếu ℋ là một hình nào đó trong mặt phẳng thì ta kí hiệu ℋ ‘ = F(ℋ) là tập các điểm M’ = F(M), với mọi điểm M thuộc ℋ. Khi đó, ta nói F là biến hình ℋ thành hình ℋ ‘, hay hình ℋ ‘ là ảnh của hình ℋ qua phép biến hình F.
– Phép biến hình biến mỗi điểm M thành chính nó được gọi là phép đồng nhất.
Ví dụ 1. Cho trước đường thẳng d, với mỗi điểm M trong mặt phẳng, gọi M’ là điểm sao cho M’ đối xứng với M qua d.
Quy tắc đặt tương ứng điểm M với điểm M’ nêu trên là một phép biến hình vì chỉ có duy nhất 1 điểm M’ thỏa mãn yêu cầu.
C. Lý thuyết Phép tịnh tiến
I. Định nghĩa.
– Định nghĩa: Trong mặt phẳng, cho vectơ . Phép biến hình biến mỗi điểm M thành điểm M’ sao cho được gọi là phép tịnh tiến theo vectơ .
– Phép tịnh tiến theo vectơ thường được kí hiệu là được gọi là vectơ tịnh tiến.
Vậy: .
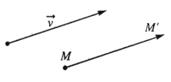
– Phép tịnh tiến theo vectơ – không chính là phép đồng nhất.
– Ví dụ 1. Cho hình vẽ sau:
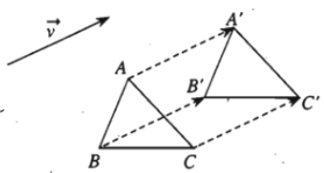
Ta có: .
II. Tính chất
– Tính chất 1. Nếu thì và từ đó suy ra M’N’ = MN.
Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.
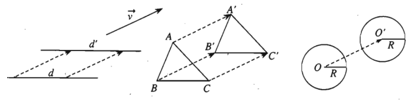
– Tính chất 2. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
III. Biểu thức tọa độ.
Trong mặt phẳng tọa độ Oxy cho vectơ . Với mỗi điểm M(x ; y) ta có M’(x’ ; y’) là ảnh của điểm M qua tịnh tiến theo vectơ .
Khi đó:
đây chính là biểu thức tọa độ của phép tịnh tiến .
Ví dụ 2. Trong mặt phẳng tọa độ Oxy, cho điểm A(1 ; – 2). Phép tịnh tiến theo vectơ biến A thành điểm A’ có tọa độ là bao nhiêu?
Lời giải:
Gọi tọa độ điểm A’ = (x’; y’).