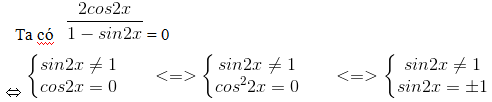50 Bài tập Phương trình lượng giác cơ bản (có đáp án) – Toán 11

Bài tập Toán 11 Chương 1 Bài 2 :Phương trình lượng giác cơ bản

A. Bài tập Phương trình lượng giác cơ bản

I. Bài tập trắc nghiệm

Bài 1: Phương trình cos23x = 1 có nghiệm là:

A. x = kπ, k ∈ Z.     

B. x =$\frac{k\pi }{2}$, k ∈ Z.

C. x =$\frac{k\pi }{3}$, k ∈ Z.     

D. x =$\frac{k\pi }{4}$, k ∈ Z.

Lời giải:

Chọn đáp án C

Bài 2: Phương trình tan( x – $\frac{\pi }{4}$) = 0 có nghiệm là:

A. x = $\frac{\pi }{4}$ + kπ, k ∈ Z.     

B. x = $\frac{3\pi }{4}$ + kπ, k ∈ Z.

C. x = kπ, k ∈ Z.     

D. x = k2π, k ∈ Z.

Lời giải:

Chọn đáp án A

Bài 3: Phương trình cot( x + $\frac{\pi }{4}$) = 0 có nghiệm là:

A. x = – $\frac{\pi }{4}$ + kπ, k ∈ Z.     

B. x = $\frac{\pi }{4}$ + kπ, k ∈ Z.

C. x = – $\frac{\pi }{4}$ + k2π, k ∈ Z.     

D. x = $\frac{\pi }{4}$ + k2π, k ∈ Z.

Lời giải:

Chọn đáp án B

Bài 4: Trong [0;π],phương trình sinx = 1 – cos2x có tập nghiệm là:

Lời giải:

Chọn đáp án D

Bài 5: Trong [0;2 π), phương trình cos2x + sinx = 0 có tập nghiệm là:

Lời giải:

Chọn đáp án B

Bài 6: Trong [0;2 π), phương trình sin2x + sinx = 0 có số nghiệm là:

A. 1      

B. 2

C. 3      

D. 4

Lời giải:

Chọn đáp án D

Bài 7: Phương trình sinx + $\sqrt{3}$cosx = 1 có số nghiệm thuộc (0;3π) là:

A. 2      

B. 3

C. 4      

D. 6

Lời giải:

Chọn đáp án B

Bài 8: Phương trình $\sqrt{2}$cos(x + $\frac{\pi }{3}$) = 1 có mấy họ nghiệm?

A. 0      

B. 2

C. 1      

D. 3

Lời giải:

Chọn đáp án B

Bài 9: Số nghiệm của phương trình sin(x +$\frac{\pi }{4}$) = 1 thuộc [0;3π] là:

A. 1      

B. 0

C. 2      

D. 3

Lời giải:

Bài 10: Phương trình sinx = cosx có số nghiệm thuộc đoạn [0;π] là:

A. 1

B. 4

C. 5

D. 2

Lời giải:

Ta có sinx = cosx ⇒ sinx = sin($\frac{\pi }{2}$ – x)

Do x ∈ [0;π] nên k = 0. Vậy chỉ có 1 nghiệm của phương trình thuộc [0;π].

Chọn đáp án A

II. Bài tập tự luận có giải

Bài 1: Phương trình sin2x = 1 có nghiệm là?

Bài 2: Phương trình sin2 $\frac{x}{3}$ = 1 có nghiệm là?

Chọn đáp án C

Bài 3 Phương trình 2cosx – $\sqrt{3}$ = 0 có tập nghiệm trong khoảng (0;2π) là?

Bài 4 Phương trình sin(πcos2x) = 1 có nghiệm là?

Bài 5 Phương trình $\frac{\cos x}{2}$ = – 1 có nghiệm là?

Bài 6: Giải các phương trình sau:

Lời giải:

b) sin3x = 1 ⇔ 3x = $\frac{\pi }{2}$ + k2π

⇔ x = $\frac{\pi }{6}$ + k($\frac{2\pi }{3}$), (k ∈ Z).

(k ∈ Z).

d) Vì –$\frac{\sqrt{3}}{2}$ = sin(-600) nên phương trình đã cho tương đương với sin (2x + 200) = sin(-600)

⇔

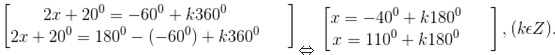
Bài 7 Với những giá trị nào của x thì giá trị của các hàm số y = sin3x và y = sinx bằng nhau?

x thỏa mãn yêu cầu bài ra khi và chỉ khi

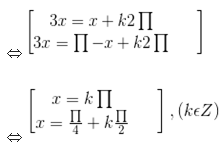
Bài 8 Giải các phương trình sau:

a) cos(x – 1) = $\frac{2}{3}$

b) cos3x = cos120

c) cos($\frac{3x}{2}$ – $\frac{\pi }{4}$) = $\frac{–1}{2}$

d) cos22x = $\frac{1}{4}$

Lời giải:

a) cos(x – 1) = $\frac{2}{3}$ ⇔ x – 1 = ±arccos$\frac{2}{3}$ + k2π

⇔ x = 1 ± arccos$\frac{2}{3}$ + k2π, (k ∈Z)

b) cos3x = cos120 ⇔ 3x = ±120 + k3600 ⇔ x = ±40 + k1200, (k ∈ Z).

c) Vì –$\frac{1}{2}$ = cos$\frac{2\pi }{3}$ nên cos($\frac{3x}{2}$ – $\frac{\pi }{4}$) = –$\frac{1}{2}$ ⇔ cos($\frac{3x}{2}$ – $\frac{\pi }{4}$) = cos$\frac{2}{3}$ ⇔ $\frac{3x}{2}$ – $\frac{\pi }{4}$ = ±$\frac{2\pi }{3}$ + k2π ⇔ x = $\frac{2}{3}$($\frac{\pi }{4}$ + $\frac{2\pi }{3}$) + $\frac{4k\pi }{3}$

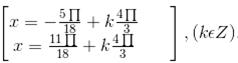
d) Sử dụng công thức hạ bậc 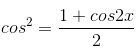 (suy ra trực tiếp từ công thức nhan đôi) ta có

cos22x = $\frac{1}{4}$ ⇔ 1 + cos$\frac{4x}{2}$ = $\frac{1}{4}$ ⇔ cos4x = –$\frac{1}{2}$

⇔ 4x = ±$\frac{2\pi }{3}$ + 2kπ ⇔ x = ±$\frac{\pi }{6}$ + $\frac{k\pi }{2}$, (k ∈ Z)

Bài 9 Giải phương trình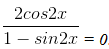 

⇔ sin2x = -1 ⇔ 2x = –$\frac{\pi }{2}$ + k2π ⇔ x = –$\frac{\pi }{4}$ + kπ, (k ∈ Z).

Bài 10 Giải các phương trình sau:

a) tan(x – 150) = $\frac{\sqrt{3}}{3}$ b) cot(3x – 1) = –$\sqrt{3}$

c) cos2x . tanx = 0 d) sin3x . cotx = 0

Lời giải:

a) Vì 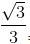= tan300 nên tan(x – 150) =  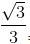⇔ tan(x – 150) = tan300 ⇔ x – 150 = 300 + k1800 ⇔ x = 450 + k1800, (k ∈ Z).

b) Vì –$\sqrt{3}$ = cot(-$\frac{\pi }{6}$) nên cot(3x – 1) = –$\sqrt{3}$ ⇔ cot(3x – 1) = cot(-$\frac{\pi }{6}$)

⇔ 3x – 1 = –$\frac{\pi }{6}$ + kπ ⇔ x = –$\frac{\pi }{18}$ + $\frac{1}{3}$ + k($\frac{\pi }{3}$), (k ∈ Z)

c) Đặt t = tan x thì cos2x = 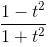 , phương trình đã cho trở thành
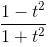. t = 0 ⇔ t ∈ {0; 1; -1} .

Vì vậy phương trình đã cho tương đương với

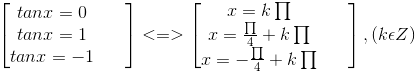
d) sin3x . cotx = 0

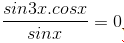⇔ Với điều kiện sinx # 0, phương trình tương đương với

sin3x . cosx = 0 ⇔ sin3x = 0; cos3x = 0

Với cosx = 0 ⇔ x = $\frac{\pi }{2}$ + kπ, k ∈ Z thì sin2x = 1 – cos2x = 1 – 0 = 1 => sinx # 0, điều kiện được thỏa mãn.

Với sin3x = 0 ⇔ 3x = kπ ⇔ x = k($\frac{\pi }{3}$), (k ∈ Z). Ta còn phải tìm các k nguyên để x = k($\frac{\pi }{3}$) vi phạm điều kiện (để loại bỏ), tức là phải tìm k nguyên sao cho sink($\frac{\pi }{3}$) = 0, giải phương trình này (với ẩn k nguyên), ta có sink($\frac{\pi }{3}$) = 0 ⇔ k($\frac{\pi }{3}$)= lπ, (l ∈ Z) ⇔ k = 3l ⇔ k : 3.

Do đó phương trình đã cho có nghiệm là x = $\frac{\pi }{2}$ + kπ, (k ∈Z) và x = k($\frac{\pi }{3}$) (với k nguyên không chia hết cho 3).

Nhận xét: Các em hãy suy nghĩ và giải thích tại sao trong các phần a, b, c không phải đặt điều kiện có nghĩa và cũng không phải tìm nghiệm ngoại lai.

III. Bài tập vận dụng 

Bài 1 Giải các phương trình sau

a) $\sin (x+2)=\frac{1}{3}$.

b) $\sin 3x=1$.

c) $\sin (\frac{2x}{3}-\frac{\pi }{3})=0$

d) $\sin (2x+{20}^0)=-\frac{\sqrt{3}}{2}$.

Bài 2 Với những giá trị nào của x thì giá trị của các hàm số y = sin3x và y = sin x bằng nhau?

Bài 3 Giải các phương trình sau:

a) $\cos (x-1)=\frac{2}{3}$.

b) $\cos 3x=\cos {12}^0$.

c). $\cos (\frac{3x}{2}-\frac{\pi }{4})=-\frac{1}{2}$.

d) ${\cos }^{2}2x=\frac{1}{4}$.

Bài 4 Giải phương trình $\frac{2\cos 2x}{1–\sin 2x}=0$

Bài 5 Giải các phương trình sau

a) $\tan (x-{15}^0)=\frac{\sqrt{3}}{3}$.

b) $\cot (3x-1)=-\sqrt{3}$.

Bài 6 Giải các phương trình sau

a) $\cos 2x.tanx=0$.

b) $\sin 3x.\cot x=0$.

Bài 7 Giải các phương trình sau

a) $\tan (x-{15}^0)=\frac{\sqrt{3}}{3}$.

b) $\cot (3x-1)=-\sqrt{3}$

Bài 8 Giải các phương trình sau

a) $\cos 2x.tanx=0$.

b) $\sin 3x.\cot x=0$.

Bài 9 Giải các phương trình sau

a) $\sin 3x-\cos 5x=0$.

b) $\tan 3x.\tan x=1$.

Bài 10 Giải các phương trình sau:

a) sin3x – cos5x = 0 b) tan3x . tanx = 1.

B. Lý thuyết Phương trình lượng giác cơ bản

I. Định nghĩa

1. Phương trình sinx = a.

Xét phương trình sinx = a (1)

– Trường hợp |a| > 1

Phương trình (1) vô nghiệm vì |sinx| ≤ 1 với mọi x.

– Trường hợp |a| ≤ 1

Gọi α là số đo bằng radian của một cung lượng giác. Khi đó, phương trình sinx = a có các nghiệm là:

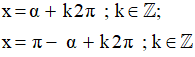
Nếu số thực α thỏa mãn điều kiện: $\left\{\begin{array}{c}\frac{-\pi }{2}\le \alpha \le \frac{\pi }{2}\\ \sin \alpha =a\end{array}\right.$ thì ta viết α = arcsina (đọc là ac-sin-a; nghĩa là cung có sin bằng a). Khi đó, các nghiệm của phương trình sinx = a được viết là:

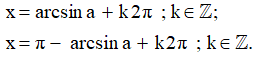
– Chú ý:

a) Phương trình sinx = sinα; với α là một số cho trước, có các nghiệm là:

$x=\alpha +\text{\hspace{0.17em}\hspace{0.17em}}k2\pi$ và $x=\pi -\alpha +\text{\hspace{0.17em}\hspace{0.17em}}k2\pi ;k\in \mathbb{Z}$

Tổng quát: 

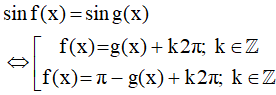
b) Phương trình sinx = sinβ0 có các nghiệm là:

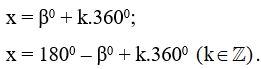
c) Trong một công thức về nghiệm của phương trình lương giác không được dùng đồng thời hai đơn vị độ và radian.

d) Các trường hợp đặc biệt:

+ Khi a = 1: Phương trình sinx = 1 có các nghiệm là $x=\frac{\pi }{2}+\text{\hspace{0.17em}\hspace{0.17em}}k2\pi ;k\in \mathbb{Z}$.

+ Khi a = – 1: Phương trình sinx = – 1 có các nghiệm là $x=-\frac{\pi }{2}+\text{\hspace{0.17em}\hspace{0.17em}}k2\pi ;k\in \mathbb{Z}$.

+ Khi a = 0:  Phương trình sinx = 0 có các nghiệm là $x=k\pi ;k\in \mathbb{Z}$.

2. Phương trình cosx = a.

– Trường hợp |a| > 1

Phương trình cosx = a vô nghiệm vì $\left|\text{cosx }\right|\le 1$ với mọi x.

– Trường hợp $\left|\text{\hspace{0.17em}a }\right|\le 1$.

Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là: $x=\pm \alpha +k2\pi ;k\in \mathbb{Z}$

– Chú ý:

a) Phương trình cosx = cosα, với α là một số cho trước, có các nghiệm là: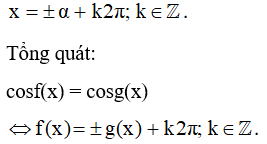 

b) Phương trình cos x= cosβ0 có các nghiệm là $x=\pm {\beta }^0+\text{\hspace{0.17em}}k{360}^0;k\in \mathbb{Z}$

c) Nếu số thực α thỏa mãn điều kiện: $\left\{\begin{array}{c}0\le \alpha \le \pi \\ \cos \alpha =a\end{array}\right.$ thì ta viết α = arccosa (đọc là ac – cosin- a, có nghĩa là cung có cosin bằng a). Khi đó, các nghiệm của phương trình cos x = a còn được viết là:

$x=\pm \arccos a\text{\hspace{0.17em}}+k2\pi ;k\in \mathbb{Z}$

d) Các trường hợp đặc biệt:

+ Khi a = 1; phương trình cosx = 1 có các nghiệm là: $x=k2\pi ;k\in \mathbb{Z}$.

+ Khi a = – 1; phương trình cosx = – 1 có các nghiệm là: $x=\pi +k2\pi ;k\in \mathbb{Z}$

+ Khi a = 0; phương trình cosx = 0 có các nghiệm là: $x=\frac{\pi }{2}+\text{\hspace{0.17em}\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$.

3. Phương trình tanx = a.

– Điều kiện xác định của phương trình là $x\ne \frac{\pi }{2}+k\pi ;k\in \mathbb{Z}$.

Kí hiệu x = arctana (đọc là ac– tang– a; nghĩa là cung có tang bằng a). Khi đó, nghiệm của phương trình tanx = a là: $x=\arctan a+\text{\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$

– Chú ý:

a) Phương trình tanx = tanα, với α là một số cho trước, có các nghiệm là:

$x=\alpha +\text{\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$

Tổng quát; tan f(x) = tan g(x) $\Rightarrow f\left(x\right)\text{\hspace{0.17em}\hspace{0.17em}}=g\left(x\right)+\text{\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$.

b) Phương trình tanx = tanβ0 có các nghiệm là: $x={\beta }^0+k{.180}^0;k\in \mathbb{Z}$.

4. Phương trình cotx = a

Điều kiện xác định của phương trình $$$x\ne k\pi ;k\in \mathbb{Z}$.

Kí hiệu x = arccota (đọc là ac– côtang – a; nghĩa là cung có côtang bằng a). Khi đó, nghiệm của phương trình cotx = a là: $x=\mathrm{arccot}a+\text{\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$

– Chú ý:

a) Phương trình cotx = cotα, với α là một số cho trước, có các nghiệm là:

$x=\alpha +\text{\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$

Tổng quát; cot f(x) = cot g(x) $\Rightarrow f\left(x\right)\text{\hspace{0.17em}\hspace{0.17em}}=g\left(x\right)+\text{\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$.

b) Phương trình cot x = cot β0 có các nghiệm là: $x={\beta }^0+k{.180}^0;k\in \mathbb{Z}$

– Ghi nhớ:

Mỗi phương trình sinx = a (|a| ≤ 1); cosx = a (|a| ≤ 1), tanx = a; cotx = a có vô số nghiệm.

Giải các phương trình trên là tìm tất cả các nghiệm của chúng.