Bài toán về khoảng cách trong không gian

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Bài toán về khoảng cách trong không gian

BÀI TOÁN KHOẢNG CÁCH TRONG HÌNH HỌC KHÔNG GIAN

Loại 1. Khoảng cách từ điểm đến mặt phẳng, một đường thẳng

A. Tóm tắt lý thuyết

1. Định nghĩa: Khoảng cách từ một điểm đến mặt phẳng (hoặc đường thẳng) bằng khoảng cách từ điểm đó tới hình chiếu vuông góc của nó lên mặt phẳng (hoặc đường thẳng).

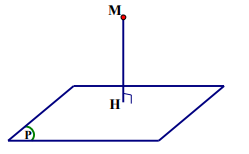
Khoảng cách từ điểm M tới mặt phẳng (P) được ký hiệu là \[d\left( {M;(P)} \right)\].

H là hình chiếu vuông góc của M lên (P) thì \[d\left( {M;(P)} \right) = MH\].

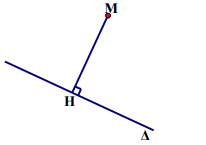
Khoảng cách từ điểm M tới đường thẳng D được ký hiệu là \[d\left( {M;\Delta } \right)\].

H là hình chiếu vuông góc của M lên D thì \[d\left( {M;\Delta } \right) = MH\].

2. Bài toán cơ bản: Nhiều bài toán tính khoảng cách từ điểm tới mặt phẳng, từ điểm tới đường thẳng có thể quy về bài toán cơ bản sau

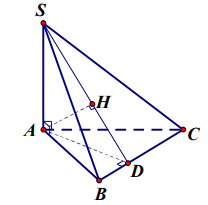
Bài toán: Cho hình chóp S.ABC có SA vuông góc với đáy. Tính khoảng cách từ điểm A đến mặt phẳng (SBC) và khoảng cách từ điểm S đến đường thẳng BC.

Cách giải

Gọi D là chân đường vuông góc hạ từ A xuống BC, H là chân đường vuông góc hạ từ A xuống SD . Ta có

SA ^ (ABC) Þ BC ^ SA, lại có BC ^ AD (do dựng) Þ BC ^ (SAD)

Þ SD ^ BC Þ d(S;BC) = SD.

Từ chứng minh trên, đã có BC ^ (SAD) Þ AH ^ BC, lại có AH ^ SD (do vẽ)

Þ AH ^ (SBC) Þ d(A;(SBC)) = AH.

 

3. Một số lưu ý

Về cách tính khoảng cách một cách gián tiếp

MN P P ( ) Þ \[MN//(P) \Rightarrow d\left( {M;(P)} \right) = d\left( {N;(P)} \right)\].

\[\left\{ {\begin{array}{*{20}{c}}{M,N \in (Q)}\\{(Q)//(P)}\end{array}} \right. \Rightarrow d\left( {M;(P)} \right) = d\left( {N;(P)} \right)\].

\[MN \cap (P) = I \Rightarrow \frac{{d\left( {M;(P)} \right)}}{{MI}} = \frac{{d\left( {N;(P)} \right)}}{{NI}}\].

Trường hợp đặc biệt: I là trung điểm của MN \[ \Rightarrow d\left( {M;(P)} \right) = d\left( {N;(P)} \right)\].

\[MN//\Delta  \Rightarrow d\left( {M;\Delta } \right) = d\left( {N;\Delta } \right)\].

\[MN \cap \Delta  = I \Rightarrow \frac{{d\left( {M;\Delta } \right)}}{{MI}} = \frac{{d\left( {N;\Delta } \right)}}{{NI}}\].

Trường hợp đặc biệt: I là trung điểm của MN \[ \Rightarrow d\left( {M;\Delta } \right) = d\left( {N;\Delta } \right)\].

Về cách sử dụng thể tích để tính khoảng cách từ điểm đến mặt phẳng: Cho hình chóp \[S.{A_1}{A_2}…{A_n}\] . Ta có

\[d\left[ {S.{A_1}{A_2}…{A_n}} \right] = \frac{{3{V_{S.{A_1}{A_2}…{A_n}}}}}{{S.{A_1}{A_2}…{A_n}}}\] .

Khoảng cách từ một đường thẳng tới mặt phẳng song song với nó: Cho \[\Delta //(P)\], M là một điểm bất kỳ trên D. Khi đó

\[d\left( {\Delta ;(P)} \right) = d\left( {M;(P)} \right)\]

Khoảng cách giữa hai mặt phẳng song song: Cho (P)//(Q), M là một điểm bất kỳ trên (P). Khi đó

\[d\left( {(P);(Q)} \right) = d\left( {M;(Q)} \right)\].

B. Một số ví dụ

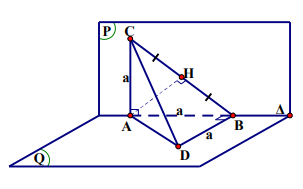
Ví dụ 1. Cho hai mặt phẳng (P) và (Q) vuông góc với nhau, cắt nhau theo giao tuyến D. Lấy A, B thuộc D và đặt AB = a. Lấy C, D lần lượt thuộc (P) và (Q) sao cho AC, BD vuông góc với D và AC = BD = a. Tính khoảng cách từ A đến mặt phẳng phẳng (BCD).

Giải

Ta có (P) ^ (Q) , (P) Ç = (Q) = D, AC Ì (P),

 AC ^ D Þ AC ^ (Q) Þ BD ^ AC.

 Lại có BD ^ AB Þ BD ^ (ABC) (1).

Gọi H là chân đường vuông góc hạ từ A xuống BC.

Vì DABC vuông cân tại A nên AH ^ BC  và \[AH = \frac{{BC}}{2} = \frac{{a\sqrt 2 }}{2}\].

Từ (1) suy ra AH ^ BD Þ AH ^ (BCD). Do đó H là chân đường vuông góc hạ từ A lên (BCD) Þ \[d\left( {A;(BCD)} \right) = AH = \frac{{a\sqrt 2 }}{2}\].

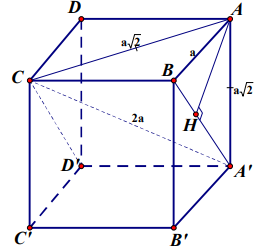
Ví dụ 2. Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông, tam giác A’AC vuông cân, A’C = a. Tính khoảng cách từ điểm A đến mặt phẳng (BCD’) theo a .

Giải

DA’AC vuông cân (tại A) nên \[AC = AA’ = \frac{{A’C}}{{\sqrt 2 }} = a\sqrt 2 \].

DABC vuông cân (tại B) nên \[AB = \frac{{AC}}{{\sqrt 2 }} = a\].

Hạ AH ^ A’B ( H Î A’B) .Ta có BC ^ ABB’A’ Þ AH ^ BC, lại có AH ^ A’B (do dựng) Þ AH ^ (BCD’).

AH là đường cao của tam giác vuông ABA’

Þ \[\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{AA{‘^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{2{a^2}}} = \frac{3}{{2{a^2}}}\]

Þ \[AH = \frac{{a\sqrt 6 }}{3}\].

Vậy \[d\left( {A;BCD’} \right) = AH = \frac{{a\sqrt 6 }}{3}\].

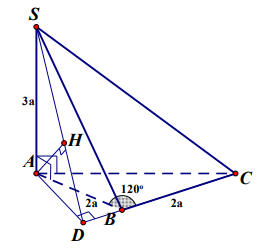
Ví dụ 3. Cho hình chóp S.ABC có SA = 3a và SA ^ (ABC). Giả sử AB = BC = 2a, \[\widehat {ABC} = {120^0}\]. Tìm khoảng cách từ A đến mặt phẳng (SBC).

Giải

Dựng AD ^ BC ( D Î BC) và AH ^ SD ( H Î SD).

Thật vậy, từ giả thiết ta có CD ^ SA, lại có CD ^ AD (do dựng) Þ CD ^ (SAD)

 Þ AH ^ CD, mà AH ^ SD Þ AH ^ (SCD) Þ H là chân đường vuông góc hạ từ A lên (SBC).

Ta có \[AD = AB\sin \widehat {ABD} = 2a\sin {60^0} = a\sqrt 3 \].

AH là đường cao của tam giác SAD vuông tại A nên:

\[\frac{1}{{A{H^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{D^2}}} = \frac{1}{{9{a^2}}} + \frac{1}{{3{a^2}}} = \frac{4}{{9{a^2}}}\]

\[ \Rightarrow AH = \frac{{3a}}{2}.\]

Vậy \[d(A;SBC) = AH = \frac{{3a}}{2}.\]

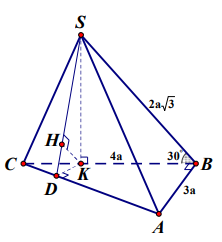
Ví dụ 4. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, BA = 3a, BC = 4a; mặt phẳng (SBC) vuông góc với mặt phẳng (ABC) . Biết SB = \[2a\sqrt 3 \]và \[\widehat {SBC} = {30^0}\]. Tính khoảng cách từ điểm B đến mặt phẳng (SAC) theo a.

Giải

Hạ SK ^ BC ( K Î BC). Vì (SBC) ^ (ABC) nên SK ^ (ABC).

Ta có \[BK = SB\cos \widehat {SBC} = 2a\sqrt 3 .\frac{{\sqrt 3 }}{2} = 3a\].

Þ \[KC = BC – BK = 4a – 3a = a.\]

Do đó nếu ký hiệu d₁, d₂ lần lượt là các khoảng cách từ các điểm B, K tới (SAC) thì 1 \[\frac{{{d_1}}}{{{d_2}}} = \frac{{BC}}{{KC}} = 4\], hay \[{d_1} = 4{d_2}\].

Hạ KD ^ AC ( D Î AC), hạ KH ^ SD ( H Î SD). Từ SK ^ (ABC) Þ AC ^ SK, lại có AC ^ KD (do dựng) Þ AC ^ (SKD) Þ KH ^ AC, mà KH ^ SD (do dựng)

Þ KH ^ (SAC) Þ \[{d_2} = KH\].

Từ DADK\[ \sim \]DABA : suy ra: \[\frac{{CK}}{{CA}} = \frac{{DK}}{{BA}}\]

Þ \[DK = \frac{{BA.CK}}{{CA}} = \frac{{3a.a}}{{5a}} = \frac{{3a}}{5}\]

(\[CA = \sqrt {B{A^2} + B{C^2}}  = \sqrt {{{(3a)}^2} + {{(4a)}^2}}  = 5a\]).

\[KS = SB.\sin \widehat {SBC} = a\sqrt 3 \]. KH là đường cao của tam giác vuông SKD nên:

\[\begin{array}{l}\frac{1}{{K{H^2}}} = \frac{1}{{K{D^2}}} + \frac{1}{{K{S^2}}} = \frac{{25}}{{9{a^2}}} + \frac{1}{{3{a^2}}} = \frac{{28}}{{9{a^2}}}\\ \Rightarrow KH = \frac{{3a\sqrt 7 }}{{14}}\end{array}\].

Vậy \[d\left( {B;(SAC)} \right) = {d_1} = 4{d_2} = 4KH = \frac{{6a\sqrt 7 }}{7}\].

Ví dụ 5. Cho lăng trụ ABCD.A₁B₁C₁D₁ có đáy ABCD là hình chữ nhật, AB = a, AD = \[a\sqrt 3 \]. Hình chiếu vuông góc của điểm A₁ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính khoảng cách từ điểm B₁ đến mặt phẳng (A₁BD) theo a.

Xem thêm