Giải SGK Toán 10 Bài 2 (Chân trời sáng tạo): Tập hợp

Giải bài tập Toán lớp 10 Bài 2: Tập hợp  

Video bài giảng Tập hợp – Chân trời sáng tạo

1. Nhắc lại về tập hợp

Giải toán lớp 10 trang 16 Tập 1 Chân trời sáng tạo

Thực hành 1 trang 16 Toán lớp 10: a) Lấy ba ví dụ về tập hợp và chỉ ra một số phần tử của chúng.

b) Với mỗi tập hợp $\mathbb{N},\mathbb{Z},\mathbb{Q},\mathbb{R}$, hãy sử dụng kí hiệu $\in$ và $\notin$để chỉ ra hai phần tử thuộc hai phần tử không thuộc tập hợp đó.

Lời giải:

a) A là tập hợp các số tự nhiên nhỏ hơn 5, khi đó $0\in A,2\in A,3\in A.$

B là tập hợp các nghiệm thực của phương trình $x^2-3x+2=0$, khi đó $1\in B,2\in B.$

C là tập hợp các thứ trong tuần, khi đó chủ nhật $\in C,$ thứ năm $\in C.$

b)

$\begin{array}{l}0\in \mathbb{N},2\in \mathbb{N},-5\notin \mathbb{N},\frac{2}{3}\notin \mathbb{N}.\\ 0\in \mathbb{Z},-5\in \mathbb{Z},\frac{2}{3}\notin \mathbb{Z},\sqrt{2}\notin \mathbb{Z}.\\ 0\in \mathbb{Q},\frac{2}{3}\in \mathbb{Q},\sqrt{2}\notin \mathbb{Q},\pi \notin \mathbb{Q}.\\ \frac{2}{3}\in \mathbb{R},\sqrt{2}\in \mathbb{R},e\notin \mathbb{R},\pi \notin \mathbb{R}.\end{array}$

Giải toán lớp 10 trang 18 Tập 1 Chân trời sáng tạo

Thực hành 2 trang 18 Toán lớp 10: Viết tập hợp sau đây dưới dạng liệt kê các phần tử và tìm số phần tử của mỗi tập hợp đó:

a) Tập hợp A các ước của 24

b) Tập hợp B gồm các chữ số trong số 1113305;

c) $C=\{n\in \mathbb{N}|n$ là bội của 5 và $n\le 30\}$

d) $D=\{x\in \mathbb{R}|x^2-2x+3=0\}$

Lời giải:

a) Số 24 có các ước là: $-24;-12;-8;-6;-4;-3;-2;-1;1;2;3;4;6;8;12;24.$ Do đó $A=\{-24;-12;-8;-6;-4;-3;-2;-1;1;2;3;4;6;8;12;24\}$, $n(A)=16.$

b) Số 1113305 gồm các chữ số: 1;3;0;5. Do đó $B=\{1;3;0;5\}$, $n(B)=4.$

c) Các số tự nhiên là bội của 5 và không vượt quá 30 là: 0; 5; 10; 15; 20; 25; 30. Do đó $C=\{0;5;10;15;20;25;30\}$, $n(C)=7.$

d) Phương trình $x^2-2x+3=0$ vô nghiệm, do đó $D=\mathrm{\varnothing }$, $n(D)=0.$

Thực hành 3 trang 18 Toán lớp 10: Viết các tập hợp sau đây dưới dạng chỉ ra tính chất đặc trưng cho các phần tử:

a) $A=\{1;3;5;...;15\}$

b) $B=\{0;5;10;.15;20;...\}$

c) Tập hợp C các nghiệm của bất phương trình $2x+5>0.$

Lời giải:

a) $A=\{x\in \mathbb{N}|x$ là số lẻ nhỏ hơn 16$\}.$

b) $B=\{x\in \mathbb{N}|x$ là bội của 5$\}.$

c) $C=\{x|2x+5>0\}.$

2. Tập con và hai tập hợp bằng nhau

HĐ Khám phá trang 18 Toán lớp 10: Trong mỗi trường hợp sau đây, các phần tử của tập hợp A có thuộc tập hợp B không? Hãy giải thích.

a) $A=\{-1;1\}$ và $B=\{-1;0;1;2\}$

b) $A=\mathbb{N}$ và $B=\mathbb{Z}$

c) A là tập hợp các học sinh nữ của lớp 10E, B là tập hợp các học sinh của lớp này.

d) A là tập hợp các loài động vật có vú, B là tập hợp các loài động vật có xương sống.

Lời giải:

a) Có vì $-1\in B,1\in B$.

b) Có vì các số tự nhiên cũng là số nguyên.

c) Có vì các học sinh nữ của lớp 10E cũng là học sinh của lớp 10E.

d) Có vì các loài động vật có vú (còn gọi là thú) là một trong các lớp thuộc các loài động vật có xương sống.

Giải toán lớp 10 trang 19 Tập 1 Chân trời sáng tạo

Thực hành 4 trang 19 Toán lớp 10: Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Chúng có bằng nhau không?

a) $A=\{-\sqrt{3};\sqrt{3}\}$ và $B=\{x\in \mathbb{R}|x^2-3=0\}$

b) C là tập hợp các tam giác đều và D là tập hợp các tam giác cân;

c) $E=\{x\in \mathbb{N}|x$ là ước của 12$\}$ và $F=\{x\in \mathbb{N}|x$ là ước của 24$\}.$

Viết tất cả các tập con của tập hợp $A=\{a;b\}.$

Phương pháp giải:

$A\subset B$ nếu mọi phần tử của A đều là phần tử của B.

$A=B$ nếu $A\subset B$ và $B\subset A$

Lời giải:

a) A là tập con củ B vì:

 $-\sqrt{3}\in \mathbb{R}$ thỏa mãn ${\left(-\sqrt{3}\right)}^2-3=0$, nên $-\sqrt{3}\in B$

$\sqrt{3}\in \mathbb{R}$ thỏa mãn ${\left(\sqrt{3}\right)}^2-3=0$, nên $\sqrt{3}\in B$

Lại có: $x^2-3=0\iff x=\pm \sqrt{3}$ nên $B=\{-\sqrt{3};\sqrt{3}\}$.

Vậy A = B.

b) C là tập hợp con của D vì: Mỗi tam giác đều đều là một tam giác cân.

$C\ne D$ vì có nhiều tam giác cân không là tam giác đều, chẳng hạn: tam giác vuông cân.

c) E là tập con của F vì $24⋮12$ nên các ước nguyên dương của 12 đều là ước nguyên dương của 24.

$E\ne F$ vì $24\in F$nhưng $24\notin E$

Thực hành 5 trang 19 Toán lớp 10: Viết tất cả các tập con của tập hợp $A=\{a;b\}.$

Lời giải:

Các tập con của tập hợp A là:

+) Tập con có 0 phần tử: $\mathrm{\varnothing }$ (tập hợp rỗng)

+) Tập hợp con có 1 phần tử: {a}, {b}

+) Tập hợp con có 2 phần tử: $A=\{a;b\}.$

Chú ý

+) Mọi tập hợp A đều có 2 tập con là: $\mathrm{\varnothing }$ và A.

Giải toán lớp 10 trang 20 Tập 1 Chân trời sáng tạo

Vận dụng trang 20 Toán lớp 10: Bạn An khẳng định rằng: Với các tập hợp A, B, C bất kì, nếu $A\subset B$ và $B\subset C$ thì $A\subset C.$ Khẳng định của bạn An có đúng không? Hãy giải thích bằng cách sử dụng biểu đồ Ven.

Lời giải:

+) Biểu diễn: $A\subset B$

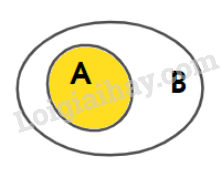
+) Sau đó, biểu diễn: $B\subset C$

Quan sát biểu đồ Ven, dễ thấy $A\subset C.$

3. Một số tập con của tập hợp số thực

Thực hành 6 trang 20 Toán lớp 10: Dùng các kí hiệu đoạn, khoảng, nửa khoảng để viết các tập hợp sau đây:

a) $\left\{x\in \mathbb{R}|-2<x<3\right\}$

b) $\left\{x\in \mathbb{R}|1\le x\le 10\right\}$

c) $\left\{x\in \mathbb{R}|-5<x\le \sqrt{3}\right\}$

d) $\left\{x\in \mathbb{R}|\pi \le x<4\right\}$

e) $\{x\in \mathbb{R}|x<\frac{1}{4}\}$

g) $\{x\in \mathbb{R}|x\ge \frac{\pi }{2}\}$

Phương pháp giải:

Lời giải:

a) Khoảng $\left(-2;3\right)$

b) Đoạn $\left[1;10\right]$

c) Nửa khoảng $(-5;\sqrt{3}]$

d) Nửa khoảng $[\pi ;4)$

e) Khoảng $\left(-\mathrm{\infty };\frac{1}{4}\right)$

g) Nửa khoảng $[\frac{\pi }{2};+\mathrm{\infty })$

Bài tập

Bài 1 trang 20 Toán lớp 10: Viết các tập hợp sau đây dưới dạng liệt kê các phần tử:

a) $A=\{x\in \mathbb{Z}||x|<5\}$

b) $B=\{x\in \mathbb{R}|2x^2-x-1=0\}$

c) $C=\{x\in \mathbb{N}|x$ có hai chữ số$\}$

Lời giải:

a) A là tập hợp các số nguyên có giá trị tuyệt đối nhỏ hơn 5.

$A=\{-4;-3;-2;-1;0;1;2;3;4\}$

b) B là tập hợp các nghiệm thực của phương trình $2x^2-x-1=0.$

$B=\{1;-\frac{1}{2}\}$

c) C là tập hợp các số tự nhiên có hai chữ số.

$C=\{10;11;12;13;...;99\}$

Giải toán lớp 10 trang 21 Tập 1 Chân trời sáng tạo

Bài 2 trang 21 Toán lớp 10: Viết các tập hợp sau đây dưới dạng liệt kê các phần tử:

a) $A=\{x\in \mathbb{Z}||x|<5\}$

b) $B=\{x\in \mathbb{R}|2x^2-x-1=0\}$

c) $C=\{x\in \mathbb{N}|x$ có hai chữ số$\}$

Lời giải:

a) A là tập hợp các số nguyên có giá trị tuyệt đối nhỏ hơn 5.

$A=\{-4;-3;-2;-1;0;1;2;3;4\}$

b) B là tập hợp các nghiệm thực của phương trình $2x^2-x-1=0.$

$B=\{1;-\frac{1}{2}\}$

c) C là tập hợp các số tự nhiên có hai chữ số.

$C=\{10;11;12;13;...;99\}$

Bài 3 trang 21 Toán lớp 10: Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập còn lại? Chúng có bằng nhau không?

a) $A=\{x\in \mathbb{N}|x<2\}$ và $B=\{x\in \mathbb{R}|x^2-x=0\}$

b) C là tập hợp các hình thoi và D là tập hợp các hình vuông

c) $E=(-1;1]$ và $F=(-\mathrm{\infty };2]$

Phương pháp giải:

$A\subset B$ nếu mọi phần tử của A đều là phần tử của B.

$A=B$ nếu $A\subset B$ và $B\subset A$

Lời giải:

a) $A=\{x\in \mathbb{N}|x<2\}=\{0;1\}$ và $B=\{x\in \mathbb{R}|x^2-x=0\}=\{0;1\}$

Vậy A = B, A là tập con của tập B và ngược lại.

b) D là tập hợp con của C vì: Mỗi hình vuông đều là một hình thoi đặc biệt: hình thoi có một góc vuông.

$C\ne D$ vì có nhiều hình thoi không là hình vuông, chẳng hạn:

c) $E=(-1;1]=\left\{x\in \mathbb{R}|-1<x\le 1\right\}$ và $F=(-\mathrm{\infty };2]=\left\{x\in \mathbb{R}|x\le 2\right\}$

E là tập con của F vì $-1<x\le 1\Rightarrow x\le 2$ .

$E\ne F$ vì $-3\in F$nhưng $-3\notin E$

Bài 4 trang 21 Toán lớp 10: Hãy viết tất cả các tập con của tập hợp $B=\{0;1;2\}.$

Phương pháp giải:

Lần lượt liệt kê các tập hợp hợp con có: 0,1,2,3 phần tử của B.

Lời giải:

Các tập con của tập hợp B là:

+) Tập con có 0 phần tử: $\mathrm{\varnothing }$ (tập hợp rỗng)

+) Các tập hợp con có 1 phần tử: {0}, {1}, {2}

+) Các tập hợp con có 2 phần tử: {0;1}, {1;2}, {0;2}

+) Tập hợp con có 3 phần tử: $B=\{0;1;2\}.$

Chú ý

+) Mọi tập hợp B đều có 2 tập con là: $\mathrm{\varnothing }$ và B.

Bài 5 trang 21 Toán lớp 10: Dùng các kí hiệu đoạn, khoảng, nửa khoảng để viết các tập hợp sau đây:

a) $\left\{x\in \mathbb{R}|-2\pi <x\le 2\pi \right\}$

b) $\left\{x\in \mathbb{R}|\left|x\right|\le \sqrt{3}\right\}$

c) $\{x\in \mathbb{R}|x<0\}$

d) $\left\{x\in \mathbb{R}|1-3x\le 0\right\}$

Phương pháp giải:

Lời giải:

a) Nửa khoảng $(-2\pi ;2\pi ]$

b) $\left\{x\in \mathbb{R}|\left|x\right|\le \sqrt{3}\right\}=\left\{x\in \mathbb{R}|-\sqrt{3}\le x\le \sqrt{3}\right\}$

Đoạn $[-\sqrt{3};\sqrt{3}]$

c) Khoảng $\left(-\mathrm{\infty };0\right)$

d) $\left\{x\in \mathbb{R}|1-3x\le 0\right\}=\left\{x\in \mathbb{R}|x\ge \frac{1}{3}\right\}$

Nửa khoảng $[\frac{1}{3};+\mathrm{\infty })$

Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Mệnh đề

Bài 3: Các phép toán trên tập hợp

Bài tập cuối chương 1

Bài 1: Bất phương trình bậc nhất hai ẩn

====== ****&**** =====