Giải SGK Toán 10 (Chân trời sáng tạo) Bài tập cuối chương 8

a) Số cách chọn 1 bạn từ nhóm 15 bạn là tổ hợp chập 1 của 15 $C_{15}^{1} = 15$ cách

b) Việc chọn 3 thành viên của nhóm đang học ở ba lớp khác nhau gồm 3 công đoạn:

Áp dụng quy tắc nhân, ta có $4.5.6 = 120$ cách chọn 3 thành viên của nhóm đang học ở ba lớp khác nhau

c) Việc chọn 2 thành viên của nhóm đang học ở hai lớp khác nhau có 3 trường hợp:

Áp dụng quy tắc cộng, ta có $20 + 24 + 30 = 74$ cách chọn 2 thành viên của nhóm đang học ở hai lớp khác nhau

Mỗi cách chọn 1 chữ số cho mật mã là 1 trong 10 cách chọn các chữ số từ 0 đến 9. Vậy có tổng cả 10 cách chọn cho mỗi chữ số

a) số tự nhiên có 6 chữ số?

b) Số tự nhiên lẻ có 6 chữ số

c) Số tự nhiên có 5 chữ số

d) Số tự nhiên có 5 chữ số lớn hơn 50 000?

Lời giải:

a) Mỗi số tự nhiên có 6 chữ số được tạo ra từ 6 thẻ số trên là mỗi cách sắp xếp 6 tấm thẻ số

Vậy có $6!$ số tự nhiên có 6 chữ số được tạo thành từ 6 tấm thẻ số đã cho

b) Để số tạo thành là số lẻ thì chữ số tận cùng là chữ số lẻ (1, 3, 5) có 3 cách chọn

Sắp xếp 5 chữ số còn lại có $5!$ cách

Áp dụng quy tắc nhân, ta có $3.5!$ số lẻ có 6 chữ số được tạo thành từ 6 tấm thẻ số

c) Mỗi số tự nhiên có 5 chữ số được tạo thành từ 6 thẻ số là mỗi cách chọn 5 tấm thẻ và sắp xếp chúng.

Vậy có $A_{6}^{5}$ số có 5 chữ số được tạo thành từ 6 thẻ số đã cho

d) Để số tạo thành lớn hơn 50 000 thì chữ số đầu tiên phải là 6 hoặc 5

Sắp xếp 4 chữ số còn lại có $A_{5}^{4}$ cách

Vậy có $2. A_{5}^{4}$ số có 5 chữ số được tạo ra từ 6 thẻ số đã cho và lớn hơn 50 000

Bài 4 trang 36 Toán lớp 10: Thực đơn tại một quán cơm văn phòng có 6 món mặn, 5 món rau và 3 món canh. Tại đây, một nhóm khách muốn chọn bữa trưa gồm cơm, 2 món mặn, 2 món rau và 1 món canh. Nhóm khách có bao nhiêu cách chọn?

Lời giải:

Để chọn được bữa cơm đủ món theo yêu cầu cần thực hiện 3 công đoạn

Công đoạn 1: Chọn 2 món mặn từ 6 món mặn có $C_{6}^{2}$ cách

Công đoạn 2: Chọn 2 món rau từ 5 món có $C_{5}^{2}$ cách

Công đoạn 3: Chọn 1 món canh từ 3 món canh có 3 cách

Áp dụng quy tắc nhân, ta có $3. C_{5}^{2} . C_{6}^{2} = 450$ cách chọn bữa cơm gồm cơm, 2 món mặn, 2 món rau và 1 món canh

Bài 5 trang 36 Toán lớp 10: Cho 9 điểm nằm trên hai đường thẳng song song như hình 3. Có bao nhiêu tam giác có các đỉnh là ba điểm trong các điểm đã cho?

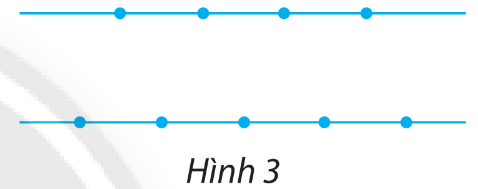
Bài 5 trang 36 Toán lớp 10 Tập 2 | Chân trời sáng tạo (ảnh 1)

Phương pháp giải:

Tam giác được tạo thành từ 3 điểm không thẳng hàng

=> chọn 2 điểm ở đường này và 1 điểm ở đường kia.

Lời giải:

Cách 1:

TH 1: Chọn 2 điểm thuộc đường thẳng có 4 điểm

Chọn 2 điểm từ đường thẳng trên có $C_{4}^{2}$ cách

Chọn 1 điểm từ đường thẳng còn lại có 5 cách

=> Số tam giác tạo thành là $5. C_{4}^{2} = 30$

TH 2: Chọn 2 điểm thuộc đường thẳng có 5 điểm

Chọn 2 điểm từ đường thẳng dưới có $C_{5}^{2}$ cách

Chọn 1 điểm từ đường thẳng còn lại có 4 cách

=> Số tam giác tạo thành là $4. C_{5}^{2} = 40$

Vậy có tất cả 70 tam giác được tạo thành.

Cách 2:

Số cách chọn 3 điểm bất kì là: $C_{9}^{3} = 84$ cách

Số cách chọn 3 điểm thẳng hàng là: $C_{4}^{3} + C_{5}^{3} = 14$ cách

=> Số cách chọn 3 điểm không thẳng hàng là: 84 – 14 = 70 (cách)

Do đó ta có thể có 70 tam giác.

Bài 6 trang 36 Toán lớp 10: Khai triển các biểu thức:

a) ${(a - \frac{b}{2})}^{4}$

b) ${(2 x^{2} + 1)}^{5}$

Phương pháp giải:

Áp dụng công thức nhị thức Newton ${(a + b)}^{n} = \sum_{k = 0}^{n} C_{n}^{k} a^{n - k} b^{k}$

Lời giải:

a) Áp dụng công thức nhị thức Newton, ta có:

$\begin{array}{l} {(a - \frac{b}{2})}^{4} = a^{4} + C_{4}^{1} . a^{3} (- \frac{b}{2}) + C_{4}^{2} . a^{2} {(- \frac{b}{2})}^{2} + C_{4}^{3} . a {(- \frac{b}{2})}^{3} + C_{4}^{4} . {(- \frac{b}{2})}^{4} \\ = a^{4} - 2 a^{3} b + \frac{3}{2} a^{2} b^{2} - \frac{1}{2} a b^{3} + \frac{1}{16} b^{4} \end{array}$

b) Áp dụng công thức nhị thức Newton, ta có:

$\begin{array}{l} {(2 x^{2} + 1)}^{5} = {(2 x^{2})}^{5} + C_{5}^{1} . {(2 x^{2})}^{4} .1 + C_{5}^{2} . {(2 x^{2})}^{3} {.1}^{2} + C_{5}^{3} . {(2 x^{2})}^{2} {.1}^{3} + C_{5}^{4} . (2 x^{2}) {.1}^{4} + 1^{5} \\ = 32 x^{10} + 80 x^{8} + 80 x^{6} + 40 x^{4} + 10 x^{2} + 1 \end{array}$

Bài 7 trang 36 Toán lớp 10: Hãy khai triển và rút gọn biểu thức ${(1 + x)}^{4} + {(1 - x)}^{4}$

Sử dụng kết quả đó để tính gần đúng biểu thức $1, 05^{4} + 0, 95^{4}$

Phương pháp giải:

Áp dụng công thức nhị thức Newton ${(a + b)}^{n} = \sum_{k = 0}^{n} C_{n}^{k} a^{n - k} b^{k}$

Lời giải:

a) Áp dụng công thức nhị thức Newton, ta có:

$\begin{array}{l} {(1 + x)}^{4} = 1^{4} + C_{4}^{1} {.1}^{3} x + C_{4}^{2} {.1}^{2} x^{2} + C_{4}^{3} .1 x^{3} + C_{4}^{4} x^{4} \\ = 1 + 4 x + 6 x^{2} + 4 x^{3} + x^{4} \end{array}$

$\begin{array}{l} {(1 - x)}^{4} = 1^{4} + C_{4}^{1} {.1}^{3} (- x) + C_{4}^{2} {.1}^{2} {(- x)}^{2} + C_{4}^{3} .1 {(- x)}^{3} + C_{4}^{4} {(- x)}^{4} \\ = 1 - 4 x + 6 x^{2} - 4 x^{3} + x^{4} \end{array}$

Suy ra

$\begin{array}{l} {(1 + x)}^{4} + {(1 - x)}^{4} = 1 + 4 x + 6 x^{2} + 4 x^{3} + x^{4} + 1 - 4 x + 6 x^{2} - 4 x^{3} + x^{4} \\ = 2 + 12 x^{2} + 2 x^{4} \end{array}$

Vậy ${(1 + x)}^{4} + {(1 - x)}^{4} = 2 + 12 x^{2} + 2 x^{4}$

Ta có: $1, 05^{4} + 0, 95^{4} = {(1 + 0, 5)}^{4} + {(1 - 0, 5)}^{4}$

Áp dụng biểu thức vừa chứng minh ${(1 + x)}^{4} + {(1 - x)}^{4} = 2 + 12 x^{2} + 2 x^{4}$ ta có:

$\begin{array}{l} 1, 05^{4} + 0, 95^{4} = {(1 + 0, 5)}^{4} + {(1 - 0, 5)}^{4} = 2 + 12.0, 5^{2} + 2.0, 5^{4} \\ = 5, 125 \end{array}$

Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Nhị thức Newton

Bài 1: Toạ độ của vecto

Bài 2: Đường thẳng trong mặt phẳng tọa độ

Bài 3: Đường tròn trong mặt phẳng tọa độ

====== ****&**** =====

Bài liên quan:

Leave a Comment Hủy