Giải bài tập Toán lớp 10 Bài 4: Tích vô hướng của hai vecto
1. Góc giữa hai vecto
Giải toán lớp 10 trang 98 Tập 1 Chân trời sáng tạo
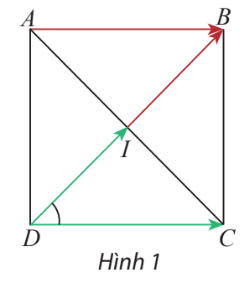
HĐ Khám phá 1 trang 98 Toán lớp 10: Cho hình vuông ABCD có tâm I (Hình 1).
a) Tính .
b) Tìm hai vectơ cùng có điểm đầu là D và điểm cuối lần lượt là I và C
c) Tìm hai vectơ có điểm đầu là D và lần lượt bằng vectơ và
Lời giải:
a) I là tâm của ABCD, suy ra
b) Vectơ có điểm đầu là D và điểm cuối là I là
Vectơ có điểm đầu là D và điểm cuối là C là
c) Vectơ có điểm đầu là D và bằng vectơ là
Vectơ có điểm đầu là D và bằng vectơ là
Giải toán lớp 10 trang 99 Tập 1 Chân trời sáng tạo
Thực hành 1 trang 99 Toán lớp 10: Cho tam giác đều ABC có H là trung điểm của cạnh BC. Tìm các góc:
.
Phương pháp giải:
Bước 1: Xác định hai vectơ cần tìm góc
Bước 2: Đưa 2 vectơ về cùng điểm đầu (chung gốc)
Bước 3: Xác định góc giữa 2 vectơ, chẳng hạn:
Lời giải:
+)
+) Dựng hình bình hành ABCD, ta có:
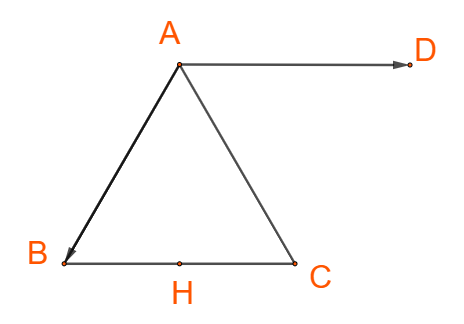
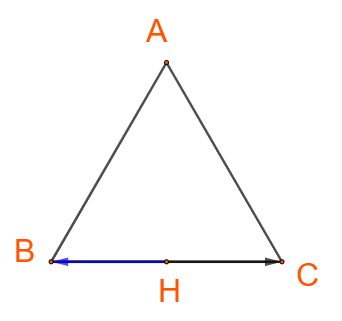
+), Ta có: ABC là tam giác đều, H là trung điểm BC nên
+) Hai vectơ và cùng hướng nên

+) Hai vectơ và ngược hướng nên
2. Tích vô hướng của hai vecto
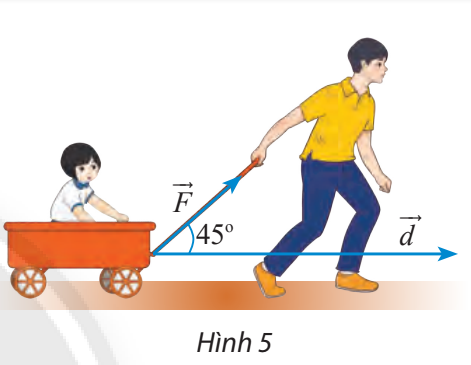
HĐ Khám phá 2 trang 99 Toán lớp 10: Một người dùng một lực có cường độ là 10 N kéo một chiếc xe đi quãng đường dài 100 m. Tính công sinh bởi lực , biết rằng góc giữa vectơ và hướng di chuyển là 45. (Công A (đơn vị: J) bằng tích của ba đại lượng: cường độ của lực , độ dài quãng đường và côsin các góc giữa vectơ và độ dịch chuyển ).
Lời giải:
Theo giả thiết ta có:
Vậy công sinh bởi lực là (J)
Giải toán lớp 10 trang 100 Tập 1 Chân trời sáng tạo
Thực hành 2 trang 100 Toán lớp 10: Cho tam giác ABC vuông cân tại A, có cạnh huyền bằng .
Tính các tích vô hướng:
Phương pháp giải:
Bước 1: Vận dụng công thức
Bước 2: Xác định độ dài cạnh AB, AC và góc giữa hai vecto
Lời giải:
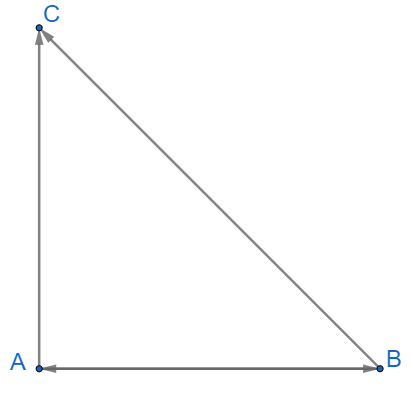
+) Ta có:
+)
Ta có:
+)
Thực hành 3 trang 100 Toán lớp 10: Hai vectơ và có độ dài lần lượt là 3 và 8 có tích vô hướng là .Tính góc giữa hai vectơ và
Phương pháp giải:
Sử dụng công thức
Lời giải:
Ta có:
Vậy góc giữa hai vectơ và là
Vận dụng 1 trang 100 Toán lớp 10: Một người dùng một lực có độ lớn là 20 N kéo một vật dịch chuyển một đoạn 50 m cùng hướng với . Tính công sinh bởi lực .
Phương pháp giải:
Công thức tính công:
Tích vô hướng:
Lời giải:
Gọi vectơ dịch chuyển của vật là , ta có .
Theo giả thiết và cùng hướng nên
Công sinh ra bởi lực được tính bằng:
(J)
3. Tính chất của tích vô hướng
Giải toán lớp 10 trang 101 Tập 1 Chân trời sáng tạo
Thực hành 4 trang 101 Toán lớp 10: Cho hai vectơ vuông góc có cùng độ dài bằng 1.
a) Tính .
b) Cho . Tính tích vô hướng và tính góc
Phương pháp giải:
Sử dụng các tính chất của tích vô hướng giữa các vectơ
Lời giải:
a) Ta có hai vectơ và vuông góc nên
+)
+)
+)
b) Sử dụng kết quả của câu a) ta có:
Vận dụng 2 trang 101 Toán lớp 10: Phân tử sulfur dioxide có cấu tạo hình chữ V, góc liên kết gần bằng . Người ta biểu diễn sự phân cực giữa nguyên tử S và nguyên tử O bằng các vectơ và có cùng phương với liên kết cộng hóa trị, có chiều từ nguyên tử S về mỗi nguyên tử O và có độ dài là 1,6 đơn vị (Hình 6). Cho biết vectơ tổng được dùng để biểu diễn sự phân cực của cả phân tử SO2. Tính độ dài của .
Phương pháp giải:
Sử dụng kết quả của ví dụ 4 trang 101
Lời giải:
Từ điểm cuối của vectơ vẽ vectơ
Suy ra
Ta có:
Vậy độ dài của là 1,6 đơn vị
Bài tập
Bài 1 trang 101 Toán lớp 10: Cho hình vuông ABCD có cạnh bằng a. Tính các tích vô hướng:
Phương pháp giải:
Bước 1: Sử dụng công thức
Bước 2: Tính và góc
Lời giải:
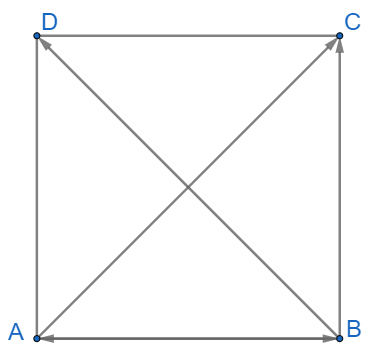
Ta có:
+)
+)
+)
+)
Chú ý
Bài 2 trang 101 Toán lớp 10: Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính:
a) ;
b) .
Phương pháp giải:
a) Bước 1: Tính đường chéo AC, BD
Bước 2: Xác định số đo góc
Bước 3: Sử dụng công thức
b) Sử dụng công thức
Lời giải:
a)
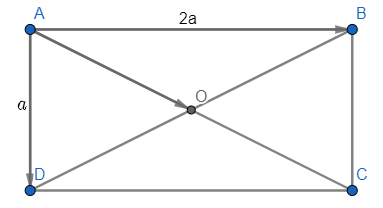
b)
Bài 3 trang 101 Toán lớp 10: Cho ba điểm O, A, B thẳng hàng và OA = a, OB = b. Tính tích vô hướng trong hai trường hợp:
a) Điểm O nằm ngoài đoạn thẳng AB;
b) Điểm O nằm trong đoạn thẳng AB.
Phương pháp giải:
Bước 1: Xác định góc giữa hai vectơ: và cùng hướng thì
Nếu và ngược hướng thì
Bước 2: Sử dụng công thức
Lời giải:
a) Ta có:

Ta thấy hai vectơ và cùng hướng nên
b) Ta có:

Ta thấy hai vectơ và ngược hướng nên
Bài 4 trang 101 Toán lớp 10: Cho đoạn thẳng AB có O là trung điểm và cho điểm M tùy ý. Chứng minh rằng:
Phương pháp giải:
Sử dụng hằng đẳng thức phân tích
Lời giải:
Ta có:
Bài 5 trang 101 Toán lớp 10: Một người dùng một lực có độ lớn là 90 N làm một vật dịch chuyển một đoạn 100 m. Biết lực hợp với hướng dịch chuyển là một góc . Tính công sinh bởi lực
Phương pháp giải:
Sử dụng công thức tính công:
Lời giải:
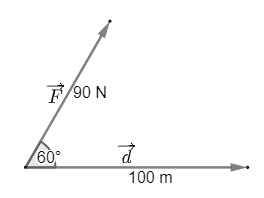
Công sinh bởi lực được tính bằng công thức
(J)
Vậy công sinh bởi lực có độ lớn bằng 4500 (J)
Bài 6 trang 101 Toán lớp 10: Cho hai vectơ có độ dài lần lượt là 3 và 4 và có tích vô hướng là – 6. Tính góc giữa hai vectơ đó.
Phương pháp giải:
Sử dụng công thức
Lời giải:
Ta cho: và
Ta có công thức:
Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Tích của một số với một vecto
Bài tập cuối chương 5
Bài 1: Số gần đúng và sai số
Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ
====== ****&**** =====