Lý thuyết Toán lớp 10 Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°

Với tóm tắt lý thuyết Toán lớp 10 Bài 1: Giá trị lượng giác của một góc từ 0° đến 180° sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 10.

Lý thuyết Toán lớp 10 Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°

A. Lý thuyết Giá trị lượng giác của một góc từ 0° đến 180°

1. Giá trị lượng giác

Mở rộng khái niệm tỉ số lượng giác đối với góc nhọn cho những góc α bất kì với 0° ≤ α ≤ 180°, ta có định nghĩa sau đây:
 

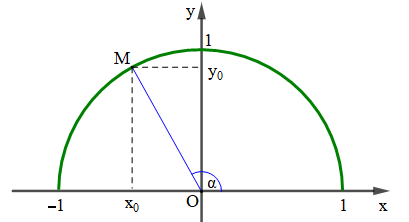
Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=\alpha$ . Gọi ($x_0$; $y_0$) là toạ độ điểm M, ta có:

– Tung độ $y_0$ của M là sin của góc α, kí hiệu là sinα = $y_0$;

– Hoành độ $x_0$ của M là côsin của góc α, kí hiệu là cosα = $x_0$;

– Tỉ số $\frac{y_0}{x_0}$ ($x_0$ ≠ 0) là tang của góc α, kí hiệu là $\tan \alpha =\frac{y_0}{x_0};$  

– Tỉ số  $\frac{y_0}{x_0}$ ($y_0$ ≠ 0) là côtang của góc α, kí hiệu là $\tan \alpha =\frac{x_0}{y_0};$

Các số sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của góc α.

Ví dụ 1. Tìm các giá trị lượng giác của góc 150°.

Hướng dẫn giải

Lấy điểm M trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=150°.$ 

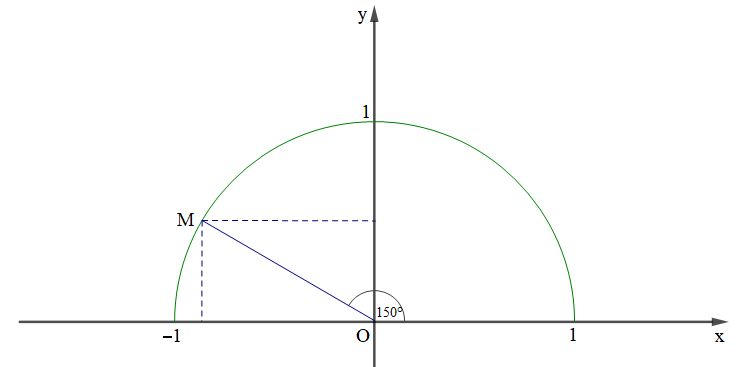Ta có  $\widehat{MOy}=150°-90°=60°$.

Khi đó ta tính được toạ độ của điểm M là $\left(-\frac{\sqrt{3}}{2};\frac{1}{2}\right).$  

Theo định nghĩa ta có:

 $\sin 150°=\frac{1}{2};$ $\text{cos150}°=-\frac{\sqrt{3}}{2};$  $\tan 150°=-\frac{1}{\sqrt{3}};$  $\cot 150°=-\sqrt{3}.$   

Chú ý: 

a) Nếu α là góc nhọn thì các giá trị lượng giác của α đều dương.

Nếu α là góc tù thì sinα > 0, cosα < 0, tanα < 0, cotα < 0.

b) tanα chỉ xác định khi α ≠ 90°.

cotα chỉ xác định khi α ≠ 0° và α ≠ 180°.

Ví dụ 2. Với α = 30° thì sinα > 0, cosα > 0, tanα > 0 và cotα > 0.

Với α = 150° (như trong Ví dụ 1) thì sinα > 0, cosα < 0, tanα < 0 và cotα < 0.

2. Quan hệ giữa các giá trị lượng giác của hai góc bù nhau

Với mọi góc α thoả mãn 0° ≤ α ≤ 180°, ta luôn có:

sin(180° ‒ α) = sinα;

cos(180° ‒ α) = ‒cosα;

tan(180° ‒ α) = ‒tanα (α ≠ 90°);

cot(180° ‒ α) = ‒cotα (0° < α < 180°).

Ví dụ 3.

a) Biết $sin60°=\frac{\sqrt{3}}{2}$. Tính cos30°, cos150°, sin120°.

b) Biết tan45° = 1. Tính tan135°.

Hướng dẫn giải

a) Ta có: $sin60°=\frac{\sqrt{3}}{2}$

Suy ra:

$c\text{os30}°=c\text{os}\left(90°-60°\right)=\sin 60°=\frac{\sqrt{3}}{2}$ (vì 30° và 60° là hai góc phụ nhau)$\text{cos150}°=cos\left(180°-30°\right)=-cos30°=-\frac{\sqrt{3}}{2}$ (vì 150° và 30° là hai góc bù nhau)$\sin 120°=\sin \left(180°-60°\right)=\sin 60°=\frac{\sqrt{3}}{2}$ (vì 120° và 60° là hai góc bù nhau);

b) Ta có: tan45° = 1.

Suy ra:

tan135° = tan(180° ‒ 45°) = ‒tan45° = ‒1 (vì 135° và 45° là hai góc bù nhau);

3. Giá trị lượng giác của một số góc đặc biệt

Dưới đây là bảng giá trị lượng giác của một số góc đặc biệt:

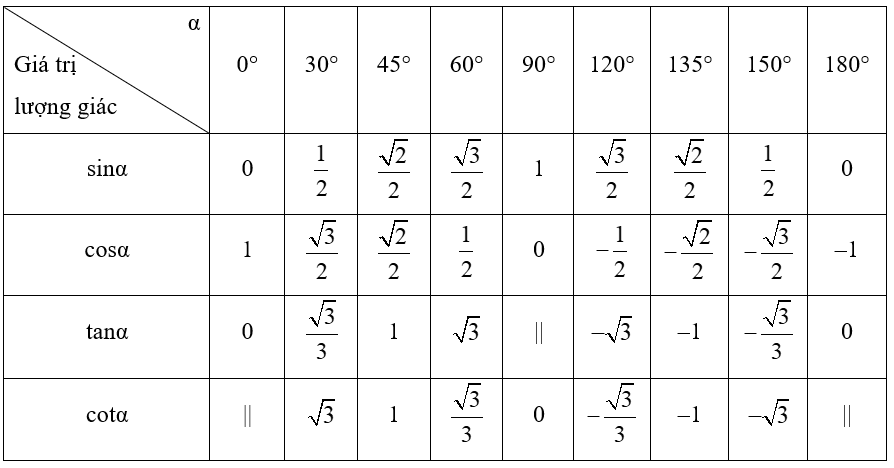Chú ý: Trong bảng, kí hiệu “||” để chỉ giá trị lượng giác không xác định.

Ví dụ 4. Tính giá trị các biểu thức sau:

a) A = $a^2$.sin90° + $b^2$.cos90° + $c^2$.cos180°;

b) B = 3 – ${\sin }^2$135° + 2$co{s}^2$120° ‒ 3${\tan }^2$150°.

Hướng dẫn giải

a) A =$a^2$.sin90° + $b^2$.cos90° + $c^2$.cos180°

A = $a^2$. 1+ $b^2$.0 +$c^2$.(‒1)

A = $a^2$ ‒ $c^2$.

b) B = 3 – sin2 135° + 2cos2 120° ‒ 3tan2 150° $B=3-{\left(\frac{\sqrt{2}}{2}\right)}^2+2.{\left(-\frac{1}{2}\right)}^2-3.{\left(-\frac{\sqrt{3}}{3}\right)}^2$

$B=3-\frac{1}{2}+2.\frac{1}{4}-3.\frac{1}{3}$

$B=3-\frac{1}{2}+\frac{1}{2}-1$

B = 2.

Ví dụ 5. Tìm góc α (0° ≤ α ≤ 180°) trong mỗi trường hợp sau:

a) $\sin \alpha =\frac{\sqrt{2}}{2}$;

b) cosα = ‒1;

c) tanα = 0;

d) $cot\alpha =-\frac{\sqrt{3}}{3}.$  

Hướng dẫn giải

a) Ta có: $\sin \alpha =\frac{\sqrt{2}}{2}$ $\Rightarrow$α = 45° hoặc α = 135°.

b) cosα = ‒1$\Rightarrow$α = 180°.

c) tanα = 0$\Rightarrow$α = 0° hoặc α = 180°.

d) $cot\alpha =-\frac{\sqrt{3}}{3}$$\Rightarrow$α = 120°.

4. Sử dụng máy tính cầm tay về tính giá trị lượng giác của một góc

Có nhiều loại máy tính cầm tay có thể giúp tính nhanh chóng giá trị lượng giác của một góc.

Chẳng hạn, ta có thể thực hiện trên một loại máy tính cầm tay như sau:

Sau khi mở máy, ẩn liên tiếp các phím $SHIFT$ $MENU$ để màn hình hiện lên bảng lựa chọn.

Ấn phím $2$ để vào chế độ cài đặt đơn vị đo góc.

Ấn tiếp phím $1$ để xác định đơn vị đo góc là “độ”.

Ấn các phím $MENU$  $1$ để vào chế độ tính toán như hình ảnh dưới đây: 
 

4.1. Tính các giá trị lượng giác của góc

Ví dụ 6. Sử dụng máy tính cầm tay, tính sin125°, cos50°12′, tan160°56’25”, cot100°.

Hướng dẫn giải

– Để tính sin125°, ta bấm liên tiếp các phím sau đây

$\sin$$1$$2$$5$$°‘ ‘‘$$)$$=$:       

Khi đó ta được kết quả hiện trên màn hình là:

Vậy sin125° ≈ 0,81915204429.

– Để tính cos50°12′, ta bấm liên tiếp các phím sau đây:

$cos50°‘ ‘‘ 1 2°‘ ‘‘)=$     

Khi đó ta được kết quả hiện trên màn hình là:

Vậy cos50°12′ ≈ 0,64010969948.

– Để tính tan160°56’25”, ta bấm liên tiếp các phím sau đây:

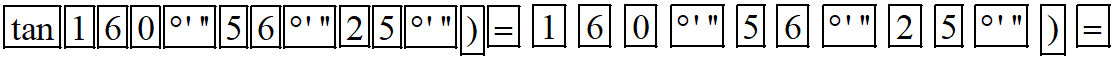
Khi đó ta được kết quả hiện trên màn hình là:

Vậy tan160°56’25” ≈ ‒0,345493396426.

– Để tính cot100°, ta bấm liên tiếp các phím sau đây: 
 Khi đó ta được kết quả hiện trên màn hình là:

Vậy cot100° ≈ ‒0,17632698071.

4.2. Xác định số đo của góc khi biết giá trị lượng giác của góc đó

Ví dụ 7. Sử dụng máy tính cầm tay, tìm α (0° < α < 180°) biết sinα = 0,51; cosα = ‒0,7$\tan \alpha =\sqrt{2};$ cotα = 1,7.

Hướng dẫn giải

– Để tìm α khi biết sinα = 0,51, ta ấn liên tiếp các phím sau đây:
         
Khi đó ta được kết quả hiện trên màn hình là:
 

Vậy với sinα = 0,51 thì α ≈ 30°39’50”.

Ta đã được học với 0° < α < 180° thì sin(180° ‒ α) = sinα nên ngoài giá trị α ≈ 30°39’50” thì ta còn có giá trị α ≈ 180° ‒ 30°39’50” ≈ 149°20’10”.

Ta bấm máy tính như sau:

– Để tìm α khi biết cosα = ‒0,7, ta ấn liên tiếp các phím sau đây:

Khi đó ta được kết quả hiện trên màn hình là:

Vậy với cosα = ‒0,7 thì α ≈ 134°25’37”.

– Để tìm α khi biết $\tan \alpha =\sqrt{2},$ ta ấn liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là: 

Vậy với $\tan \alpha =\sqrt{2}$ thì α ≈ 54°44’8”.

– Để tìm α khi biết cotα = 1,7, trước hết ta tính  , ta ấn liên tiếp các phím sau đây: 
 

Khi đó ta được kết quả hiện trên màn hình là:

Sau đó ta bấm liên tiếp các phím:Khi đó ta được kết quả hiện trên màn hình là:

Vậy với cotα = 1,7 thì α ≈ 30°27’56”.

B. Bài tập tự luyện

Bài 1. Tính giá trị biểu thức:

a) A = sin30°.cos45°.sin60° ‒ cos120°.tan135°.cot150°.

b) B = cos0° + cos20° + cos40° + … + cos160° + cos180°;

c) $C=sin\left(180°-x\right)-cos\left(90°-x\right)+si{n}^{2}x.\frac{1}{{\sin }^2\left(90°-x\right)}–ta{n}^{2}x.$

Hướng dẫn giải

a) A = sin30°.cos45°.sin60° ‒ cos120°.tan135°.cot150°

 $A=\frac{1}{2}.\frac{\sqrt{2}}{2}.\frac{\sqrt{3}}{2}-\left(-\frac{1}{2}\right).\left(-1\right).\left(-\sqrt{3}\right)$

 $A=\frac{\sqrt{6}}{8}+\frac{\sqrt{3}}{2}$

 $A=\frac{\sqrt{6}+4\sqrt{3}}{8}$

b) B = cos0° + cos20° + cos40° + … + cos160° + cos180°

B = (cos0° + cos180°) + (cos20° + cos160°) + … + (cos80° + cos100°)

B = (cos0° ‒ cos0°) + (cos20° ‒ cos20°) + … + (cos80° ‒ cos80°)  (hai góc bù nhau)

B = 0.

c) $C=sin\left(180°-x\right)-cos\left(90°-x\right)+si{n}^{2}x.\frac{1}{{\sin }^2\left(90°-x\right)}–ta{n}^{2}x.$$C=\sin x-\sin x+si{n}^{2}x.\frac{1}{{\text{cos}}^{2}x}–ta{n}^{2}x$

C = 0 + tan2x ‒ tan2x

C = 0.

Bài 2. Cho góc α  (0° ≤ α ≤ 180°) với $\tan \alpha =-\sqrt{3}$. Tính giá trị biểu thức:$M=cos\alpha +co{t}^2\alpha -\frac{1}{{\sin }^2\alpha }.$

Hướng dẫn giải

Với $\tan \alpha =-\sqrt{3}$ ta có α = 120°.

Suy ra: $sin\alpha =\frac{\sqrt{3}}{2};cos\alpha =-\frac{1}{2};\cot \alpha =-\frac{\sqrt{3}}{3}.$

Do đó: 
$M=cos\alpha +co{t}^2\alpha -\frac{1}{{\sin }^2\alpha }$ 
$M=-\frac{1}{2}+{\left(-\frac{\sqrt{3}}{3}\right)}^2-\frac{1}{{\left(\frac{\sqrt{3}}{2}\right)}^2}$ 
$M=-\frac{1}{2}+\frac{1}{3}-\frac{4}{3}$ 
$M=-\frac{3}{2}.$

Vậy $M=-\frac{3}{2}.$

Bài 3.

a) Chứng minh rằng với mọi góc 0° ≤ α ≤ 180° ta luôn có: sin2α + cos2α = 1.

b) Cho tam giác ABC. Chứng minh rằng:

$\frac{{\sin }^3\frac{B}{2}}{cos\left(\frac{A+C}{2}\right)}+\frac{co{s}^3\frac{B}{2}}{\sin \left(\frac{A+C}{2}\right)}-\frac{cos\left(A+C\right)}{\sin B}.\tan B=2.$

Hướng dẫn giải

a) Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=\alpha$. Gọi ($x_0$; $y_0$) là toạ độ điểm M, ta có:

– Tung độ $y_0$ của M là sin của góc α, kí hiệu là sinα = $y_0$;

– Hoành độ $x_0$ của M là côsin của góc α, kí hiệu là cosα = $x_0$;

Gọi H và K lần lượt là hình chiếu của M lên Ox và Oy.
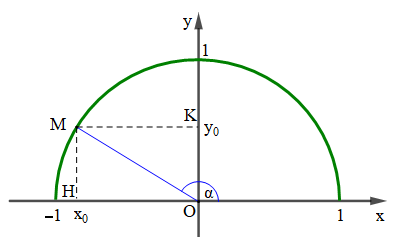 Khi đó ta có: OH = $x_0$ = cosα, MH = OK = $y_0$ = sinα, OM = 1.

Tam giác OMH vuông tại H, áp dụng định lí Pythagore ta có:

$M{H}^2+O{H}^2=O{M}^2$

Hay sin2α + cos2α = 1.

Vậy sin2α + cos2α = 1.

b) Vì $\widehat{A}+\widehat{B}+\widehat{C}$ = 180° (định lí tổng ba góc trong tam giác) nên:  $\widehat{A}+\widehat{C}$ = 180° ‒ $\widehat{B}$.

Suy ra $\frac{\widehat{A}+\widehat{C}}{2}=\frac{180°-\widehat{B}}{2}=90°-\frac{\widehat{B}}{2}$.

Ta có:

$\frac{{\sin }^3\frac{B}{2}}{cos\left(\frac{A+C}{2}\right)}+\frac{co{s}^3\frac{B}{2}}{\sin \left(\frac{A+C}{2}\right)}-\frac{cos\left(A+C\right)}{\sin B}.\tan B$   $=\frac{{\sin }^3\frac{B}{2}}{cos\left(90°-\frac{B}{2}\right)}+\frac{co{s}^3\frac{B}{2}}{\sin \left(90°-\frac{B}{2}\right)}-\frac{cos\left(180°-B\right)}{\sin B}.\tan B$

$=\frac{{\sin }^3\frac{B}{2}}{\sin \frac{B}{2}}+\frac{co{s}^3\frac{B}{2}}{cos\frac{B}{2}}-\frac{-\cos B}{\sin B}.\tan B$

$={\sin }^2\frac{B}{2}+co{s}^2\frac{B}{2}+\frac{\cos B}{\sin B}.\tan B$

$=\left({\sin }^2\frac{B}{2}+co{s}^2\frac{B}{2}\right)+\frac{\cos B}{\sin B}.\frac{\sin B}{\cos B}$

= 1 + 1 (do sin2α + cos2α = 1 theo câu a)

= 2

Vậy $\frac{{\sin }^3\frac{B}{2}}{cos\left(\frac{A+C}{2}\right)}+\frac{co{s}^3\frac{B}{2}}{\sin \left(\frac{A+C}{2}\right)}-\frac{cos\left(A+C\right)}{\sin B}.\tan B=2.$

Bài 4. Sử dụng máy tính cầm tay để thực hiện các yêu cầu sau:

a) Tính sin95°7’16”, cos22°12’21”, tan27°22′, cot24°.

b) Tìm β biết (0° < β < 180°) trong các trường hợp:

i) cosβ = ‒0,19;

ii) tanβ = 1,2.

Hướng dẫn giải

a) – Để tính sin95°7’16”, ta bấm liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là: 

Vậy sin95°7’16” ≈ 0,99600824395.

– Để tính cos22°12’21”, ta bấm liên tiếp các phím sau đây: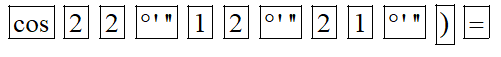 
Khi đó ta được kết quả hiện trên màn hình là: 

Vậy cos22°12’21” ≈ 0,92583211171.

– Để tính tan27°22′, ta bấm liên tiếp các phím sau đây: 
Khi đó ta được kết quả hiện trên màn hình là: 

Vậy tan27°22′ ≈ 0,51761289576.

– Để tính cot24°, ta bấm liên tiếp các phím sau đây: 
Khi đó ta được kết quả hiện trên màn hình là:

Vậy cot24° ≈ 2,2460367739.

b) – Để tìm β khi biết cosβ = ‒0,19, ta ấn liên tiếp các phím sau đây           
Khi đó ta được kết quả hiện trên màn hình là:
 

Vậy với cosβ = ‒0,19 thì β ≈ 100°57’10”.

– Để tìm β khi biết tanβ = 1,2, ta ấn liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là: 

Vậy với tanβ = 1,2 thì β ≈ 50°11’40”.

====== ****&**** =====