Với tóm tắt lý thuyết Toán lớp 10 Bài 4: Ba đường conic trong mặt phẳng tọa độ sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 10.
Lý thuyết Toán lớp 10 Bài 4: Ba đường conic trong mặt phẳng tọa độ
A. Lý thuyết Ba đường conic trong mặt phẳng tọa độ
1. Elip
1.1. Nhận biết elip
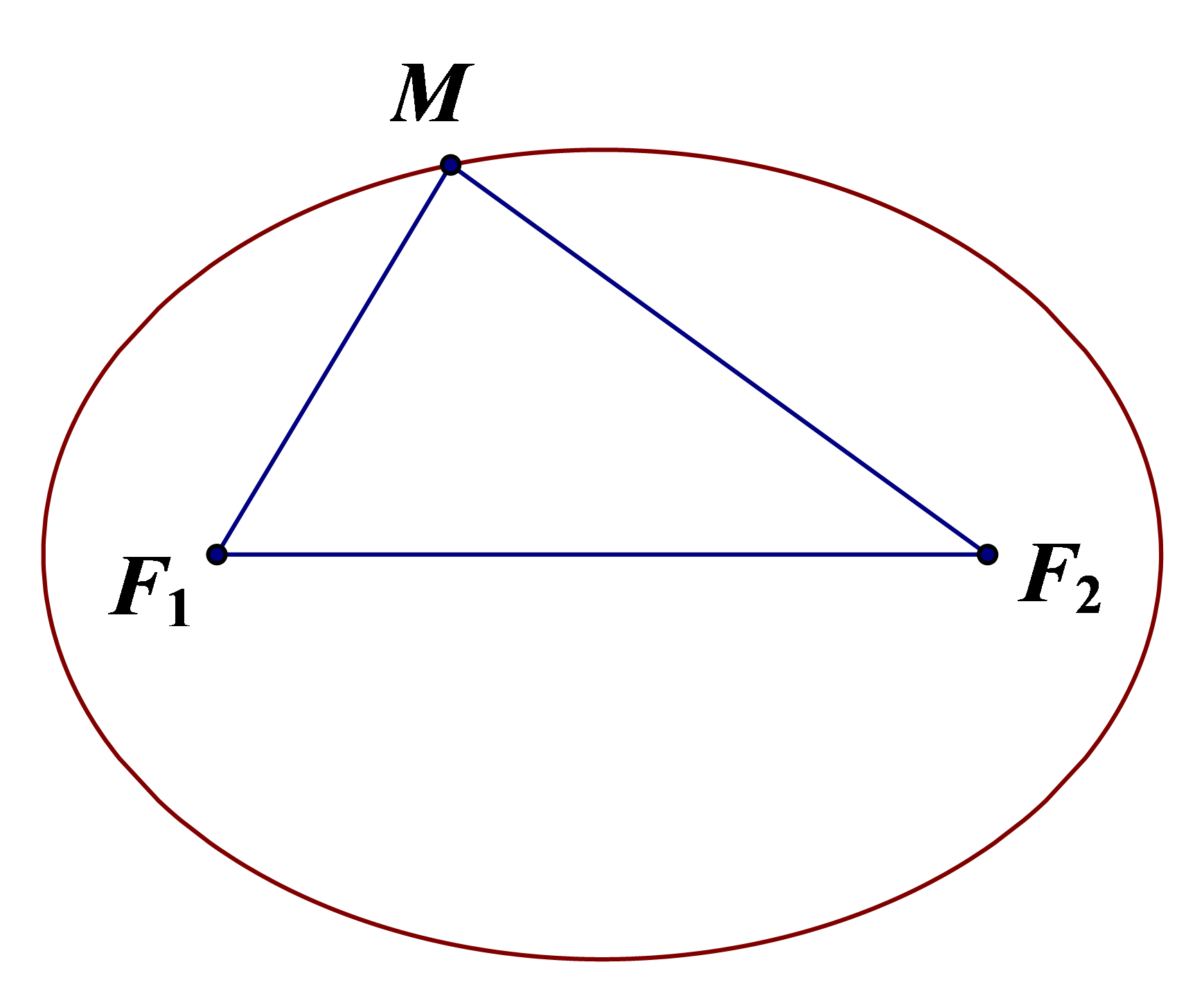
Cho hai điểm cố định F1, F2 và một độ dài không đổi 2a lớn hơn F1F2. Elip (E) là tập hợp các điểm M trong mặt phẳng sao cho F1M + F2M = 2a.
Các điểm F1 và F2 gọi là các tiêu điểm của elip.
Độ dài F1F2 = 2c gọi là tiêu cự của elip (a > c).
1.2. Phương trình chính tắc của elip
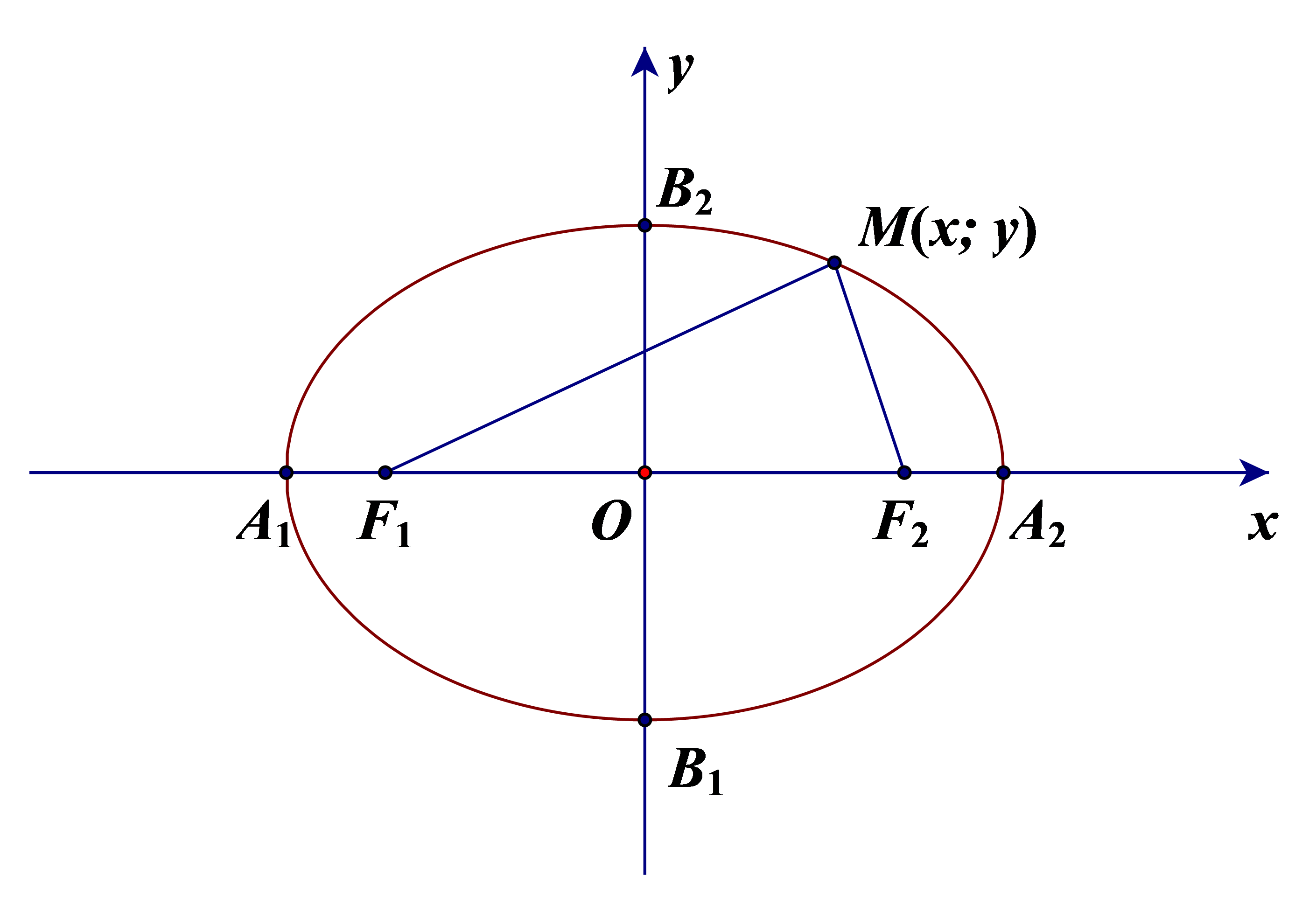
Cho elip (E) có các tiêu điểm F1 và F2 và đặt F1F2 = 2c. Chọn hệ trục tọa độ Oxy sao cho F1(–c; 0) và F2(c; 0).
Người ta chứng minh được:
(1),
trong đó .
Phương trình (1) gọi là phương trình chính tắc của elip.
Chú ý:
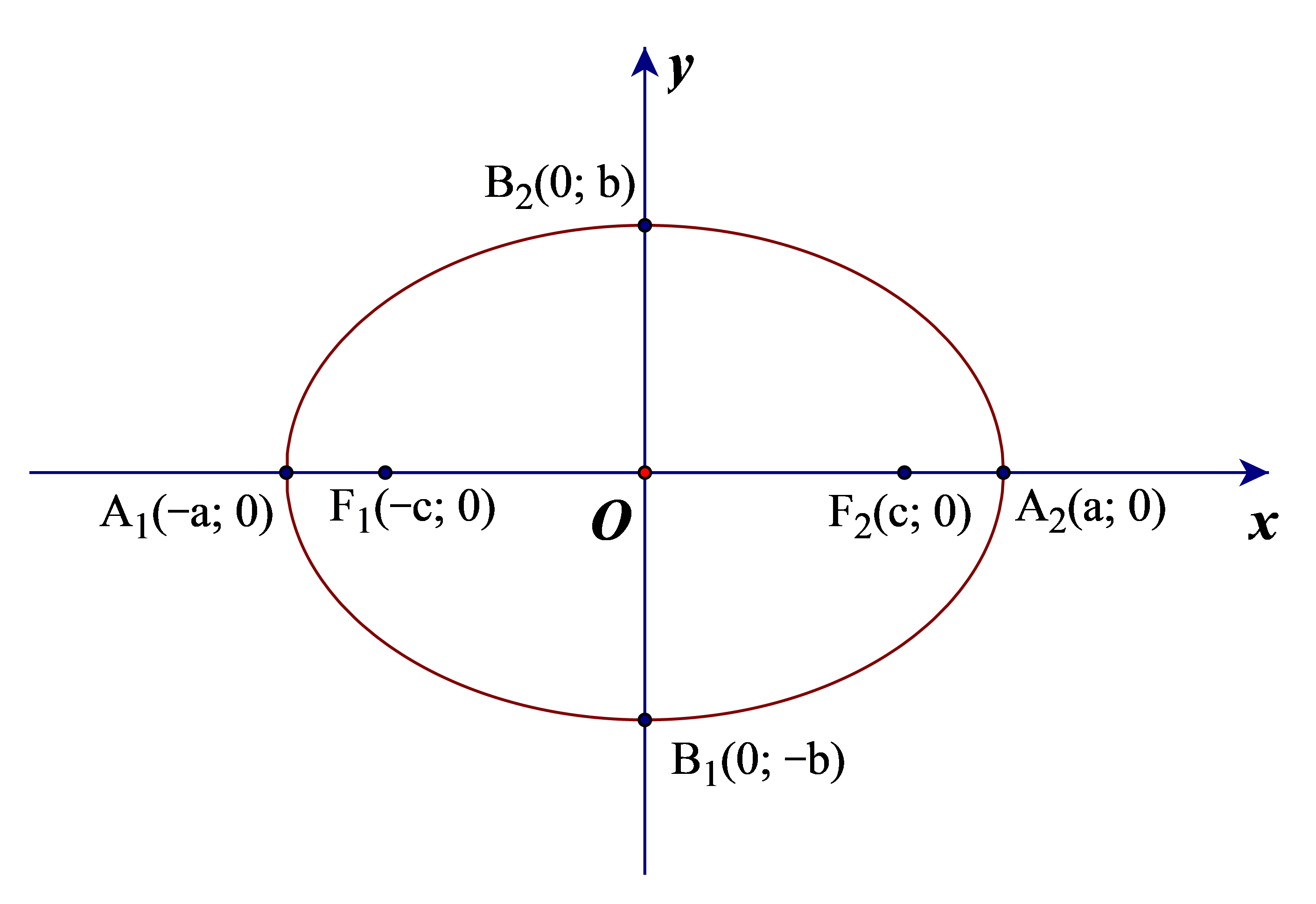
• (E) cắt Ox tại hai điểm A1(–a; 0), A2(a; 0) và cắt Oy tại hai điểm B1(0; –b), B2(0; b).
• Các điểm A1, A2, B1, B2 gọi là các đỉnh của elip.
• Đoạn thẳng A1A2 = 2a gọi là trục lớn, đoạn thẳng B1B2 = 2b gọi là trục nhỏ của elip.
• Giao điểm O của hai trục gọi là tâm đối xứng của elip.
• Nếu M(x; y) ∈ (E) thì |x| ≤ a, |y| ≥ b.
Ví dụ: Cho elip (E) có độ dài trục lớn bằng 10, tỉ số giữa tiêu cự và độ dài trục lớn là .
a) Tính độ dài trục nhỏ của elip.
b) Viết phương trình chính tắc của elip.
Hướng dẫn giải
a) Ta có độ dài trục lớn bằng 10. Ta suy ra 2a = 10.
Suy ra a = 5.
Theo đề, ta có tỉ số giữa tiêu cự và độ dài trục lớn là .
Suy ra .
.
Ta có .
Suy ra 2b = 2.3 = 6.
Vậy độ dài trục nhỏ của elip (E) bằng 6.
b) Ta có a = 5 và b = 3.
Phương trình chính tắc của elip (E) là: .
2. Hypebol
2.1. Nhận biết hypebol
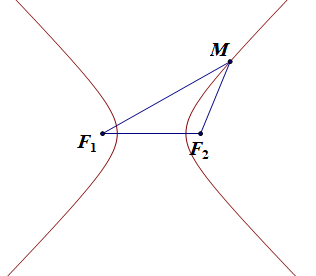
Cho hai điểm cố định F1, F2 và một độ dài không đổi 2a nhỏ hơn F1F2. Hypebol (H) là tập hợp các điểm M trong mặt phẳng sao cho |F1M – F2M| = 2a.
Các điểm F1 và F2 gọi là các tiêu điểm của hypebol.
Độ dài F1F2 = 2c gọi là tiêu cự của hypebol (c > a).
2.2. Phương trình chính tắc của hypebol
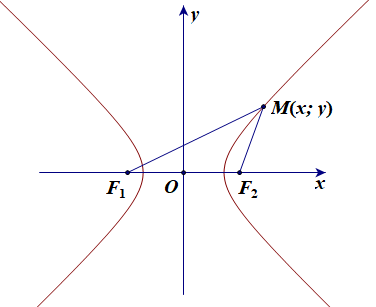
Cho hypebol (H) có các tiêu điểm F1 và F2 và đặt F1F2 = 2c. Điểm M thuộc hypebol (H) khi và chỉ khi |F1M – F2M| = 2a. Chọn hệ trục tọa độ Oxy sao cho F1(–c; 0) và F2(c; 0).
Người ta chứng minh được:
(2),
trong đó .
Phương trình (2) gọi là phương trình chính tắc của hypebol.
Chú ý:
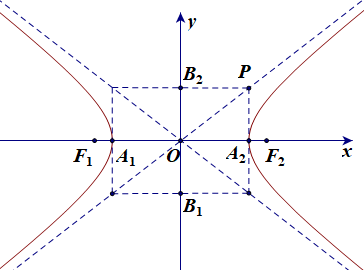
• (H) cắt Ox tại hai điểm A1(–a; 0) và A2(a; 0). Nếu ta vẽ hai điểm B1(0; –b) và B2(0; b) vào hình chữ nhật OA2PB2 thì .
• Các điểm A1, A2 gọi là các đỉnh của hypebol.
• Đoạn thẳng A1A2 = 2a gọi là trục thực, đoạn thẳng B1B2 = 2b gọi là trục ảo của hypebol.
• Giao điểm O của hai trục là tâm đối xứng của hypebol.
• Nếu M(x; y) ∈ (H) thì x ≤ –a hoặc x ≥ a.
Ví dụ: Cho hypebol (H) có một tiêu điểm F2(8; 0) và (H) đi qua điểm A(5; 0). Viết phương trình chính tắc của hypebol (H).
Hướng dẫn giải
Phương trình chính tắc của (H) có dạng , trong đó a, b > 0.
Vì A(5; 0) ∈ (H) nên ta có . Suy ra a = 5.
Do (H) có một tiêu điểm F2(8; 0) nên ta có c = 8.
Suy ra .
Vậy phương trình chính tắc của (H) là .
3. Parabol
3.1. Nhận biết parabol
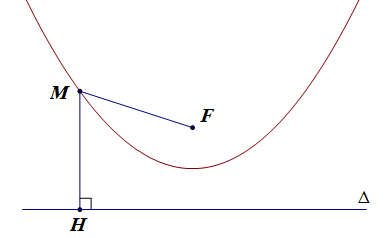
Cho một điểm F và một đường thẳng ∆ cố định không đi qua F. Parabol (P) là tập hợp các điểm M cách đều F và ∆.
F gọi là tiêu điểm và ∆ gọi là đường chuẩn của parabol (P).
3.2. Phương trình chính tắc của parabol
Cho parabol (P) có tiêu điểm F và đường chuẩn ∆. Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên p > 0.
Chọn hệ trục tọa độ Oxy sao cho và ∆: .
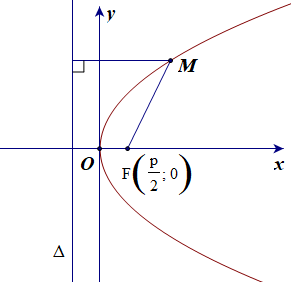
Người ta chứng minh được:
M(x; y) ∈ (P) ⇔ y2 = 2px (3).
Phương trình (3) gọi là phương trình chính tắc của parabol.
Chú ý:
• O gọi là đỉnh của parabol (P).
• Ox gọi là trục đối xứng của parabol (P).
• p gọi là tham số tiêu của parabol (P).
• Nếu M(x; y) ∈ (P) thì x ≥ 0 và M’(x; –y) ∈ (P).
Ví dụ: Viết phương trình chính tắc của parabol (P), biết (P) có đường chuẩn ∆: x + 4 = 0.
Hướng dẫn giải
(P) có đường chuẩn ∆: x + 4 = 0.
Ta suy ra .
Khi đó p = 2.4 = 8.
Vậy phương trình chính tắc của parabol (P) là: y2 = 16x.
B. Bài tập tự luyện
Bài 1. Tìm tiêu điểm của các đường conic sau:
a) Elip (E): .
b) Hypebol (H): .
c) Parabol (P): y2 = 2x.
Hướng dẫn giải
a) Phương trình (E) có dạng: , với a = 10, b = 8.
Suy ra .
Vậy elip (E) có các tiêu điểm F1(–6; 0) và F2(6; 0).
b) Phương trình (H) có dạng: , với a = 2, b = 3.
Suy ra .
Vậy hypebol (H) có các tiêu điểm và .
c) Phương trình parabol (P) có dạng: y2 = 2px, với p = 1.
Ta suy ra .
Vậy parabol (P) có tiêu điểm .
Bài 2. Viết phương trình chính tắc của các đường conic trong các trường hợp sau:
a) Elip (E) đi qua điểm B(0; 3) và có tiêu cự bằng 6.
b) Hypebol (H) đi qua điểm M(2; 4) và có độ dài trục ảo bằng 8.
c) Parabol (P) có tiêu điểm F(10; 0).
Hướng dẫn giải
a) Phương trình elip (E) có dạng: , với a, b > 0.
Vì B(0; 3) ∈ (E) nên ta có .
Suy ra b = 3.
Theo đề, ta có tiêu cự bằng 6. Suy ra 2c = 6. Nghĩa là c = 3.
Ta có .
Vậy phương trình elip (E) là: .
b) Phương trình hypebol (H) có dạng: , với a, b > 0.
Vì (H) có độ dài trục ảo bằng 8 nên ta có 2b = 8. Suy ra b = 4.
Khi đó b2 = 16.
Vì M(2; 4) ∈ (H) nên ta có .
.
.
Vậy phương trình chính tắc của (H) là: .
c) Parabol (P) có tiêu điểm F(10; 0) nên ta có .
Suy ra p = 2.10 = 20.
Vậy phương trình chính tắc của (P) là: y2 = 40x.
Bài 3. Cho elip (E): và C(2; 0). Tìm A, B thuộc (E), biết A có tung độ dương, A và B đối xứng nhau qua trục hoành và ∆ABC cân tại A.
Hướng dẫn giải
Gọi A(x0; y0) với y0 > 0.
Vì A, B đối xứng nhau qua trục hoành nên ta có tọa độ B(x0; –y0).
Vì A ∈ (E) nên ta có .
(1).
Với A(x0; y0), B(x0; –y0) và C(2; 0) ta có:
và
Vì ∆ABC cân tại A nên ta có AB2 = AC2.
⇔ (–2y0)2 = (2 – x0)2 + (–y0)2
(2).
Thế (1) vào (2), ta được: .
.
⇔ x0 = 2 hoặc .
• Với x0 = 2, ta có . Suy ra y0 = 0.
Khi A(2; 0).
Lúc này A ≡ C (mâu thuẫn vì ba điểm A, B, C tạo thành một tam giác).
Vậy ta loại trường hợp x0 = 2.
• Với , ta có . Suy ra .
Vì y0 > 0 nên ta nhận .
Vậy thỏa mãn yêu cầu bài toán.
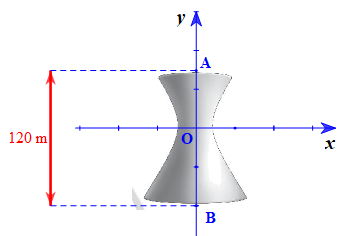
Bài 4. Một tháp triển lãm có mặt cắt là một hypebol có phương trình \. Biết chiều cao của tháp là 120 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng khoảng cách từ tâm đối xứng đến đáy. Chọn hệ trục toạ độ như hình vẽ dưới đây, tính bán kính nóc và bán kính đáy của tháp. (Làm tròn kết quả đến hàng phần mười).
 Hướng dẫn giải
Hướng dẫn giải
Theo bài ra, khoảng cách từ nóc tháp đến tâm O bằng khoảng cách từ tâm O đến đáy nên ta có: OA = OB và OA + OB = 120 m.
Suy ra: OA = 48 m, OB = 72 m.
Þ A (0; 48), B(0 ; –72).
Thay y = 48 vào phương trình , ta được:
Þ x2 = 1 525 ⇒ x ≈ 39,1 hoặc x ≈ –39,1.
Suy ra bán kính nóc khoảng 39,1 (m).
Thay y = –72 vào phương trình ta được:
Þ x2 = 2 650 ⇒ x ≈ 51,5 hoặc x ≈ –51,5.
Suy ra bán kính đáy khoảng 51,5 (m).
Vậy bán kính nóc và bán kính đáy của tháp triển lãm lần lượt là 39,1 (m) và 51,5 (m).
====== ****&**** =====