Giải SGK Toán 7 Bài 34 (Kết nối tri thức): Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác

Giải bài tập Toán lớp 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác

Giải Toán 7 trang 72 Tập 2

1. Sự đồng quy của ba đường trung tuyến trong một tam giác

Câu hỏi trang 72 Toán lớp 7: Mỗi tam giác có mấy đường trung tuyến?

Phương pháp giải:

Đoạn thẳng nối đỉnh của tam giác với trung điểm cạnh đối diện được gọi là một đường trung tuyến của tam giác.

Lời giải:

Tương ứng với mỗi đỉnh của tam giác có 1 đường trung tuyến nên mỗi tam giác có 3 đường trung tuyến.

HĐ 1 trang 72 Toán lớp 7: Hãy lấy một mảnh giấy hình tam giác, gấp giấy đánh dấu trung điểm của các cạnh. Sau đó, gấp giấy để được các nếp gấp đi qua đỉnh và trung điểm của cạnh đối diện ( tức là các đường trung tuyến của tam giác). Mở tờ giấy ra, quan sát và cho biết ba nếp gấp ( ba đường trung tuyến) có cùng đi qua một điểm không?

HĐ 1 trang 72 Toán lớp 7 Tập 2 | Kết nối tri thức (ảnh 1)

Phương pháp giải:

Gấp theo hướng dẫn

Lời giải:

Ba nếp gấp đi qua cùng một điểm.

Giải Toán 7 trang 73 Tập 2

HĐ 2 trang 73 Toán lớp 7: Trên mảnh giấy kẻ ô vuông, mỗi chiều 10 ô, hãy đếm dòng, đánh dấu các đỉnh A,B,C rồi vẽ tam giác ABC. (H.9.29)

Vẽ hai đường trung tuyến BN, CP, chúng cát nhau tại G, tia AG cắt cạnh BC tại M.

AM có phải là đường trung tuyến của tam giác ABC không?
Hãy xác định các tỉ số $\frac{G A}{M A}; \frac{G B}{N B}; \frac{G C}{P C}$

Phương pháp giải:

Kiểm tra M có là trung điểm của BC không?
Đếm các độ dài và tính tỉ số.

Lời giải:

Ta có: MB = MC và M nằm giữa B và C nên M là trung điểm của BC.

Do đó, AM có là đường trung tuyến của tam giác ABC

$\begin{array}{l} \frac{G A}{M A} = \frac{6}{9} = \frac{2}{3}; \\ \frac{G B}{N B} = \frac{2}{3}; \\ \frac{G C}{P C} = \frac{2}{3} \end{array}$

Luyện tập 1 trang 73 Toán lớp 7: Trong tam giác ABC ở ví dụ 1, cho trung tuyến BN và GN = 1 cm. Tính GB và NB.

Phương pháp giải:

Sử dụng định lí về sự đồng quy của ba đường trung tuyến của tam giác.

Lời giải:

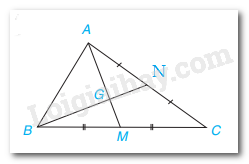
Luyện tập 1 trang 73 Toán lớp 7 Tập 2 | Kết nối tri thức (ảnh 1)

Vì G là trọng tâm của tam giác ABC nên $\frac{G B}{N B} = \frac{2}{3} \Leftrightarrow G B = \frac{2}{3} N B$

Ta có: GN = NB – GB = $N B - \frac{2}{3} N B = \frac{1}{3} N B$

Mà GN = 1 cm nên 1 = $\frac{1}{3} . N B \Rightarrow N B = 3$ ( cm)

$G B = \frac{2}{3} N B = \frac{2}{3} .3 = 2$ ( cm)

Vậy GB = 2 cm, NB = 3 cm.

Giải Toán 7 trang 74 Tập 2

Tranh luận trang 74 Toán lớp 7:

Tranh luận trang 74 Toán lớp 7 Tập 2 | Kết nối tri thức (ảnh 2)

Phương pháp giải:

Sử dụng định lí về sự đồng quy của ba đường trung tuyến của tam giác.

Lời giải:

Cách 1: Tìm giao điểm của 2 đường trung tuyến.

Cách 2: Vẽ 1 đường trung tuyến. Lấy điểm G cách đỉnh một khoảng bằng $\frac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh đó. Ta được G là trọng tâm tam giác.

Vận dụng 1 trang 74 Toán lớp 7: Trong tình huống mở đầu, người ta chứng minh được G chính là trọng tâm của tam giác ABC. Em hãy cắt một mảnh bìa hình tam giác. Xác định trọng tâm của tam giác và đặt mảnh bìa đó lên một giá nhọn tại trọng tâm vừa xác định. Quan sát xem mảnh bìa có thăng bằng không?

Phương pháp giải:

Bước 1: Cắt mảnh bìa hình tam giác.

Bước 2: Kẻ 2 đường trung tuyến của tam giác ABC, chúng cắt nhau tại G.

Bước 3: Đặt mảnh bìa đó lên một giá nhọn tại trọng tâm G.

Lời giải:

Cắt mảnh bìa hình tam giác. Kẻ 2 đường trung tuyến của tam giác ABC, chúng cắt nhau tại G.

Đặt mảnh bìa đó lên một giá nhọn tại trọng tâm G thì thấy mảnh bìa thăng bằng.

2. Sự đồng quy của ba đường phân giác trong một tam giác

Câu hỏi trang 74 Toán lớp 7: Mỗi tam giác có mấy đường phân giác?

Phương pháp giải:

Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm D thì AD là đường phân giác của tam giác ABC.

Lời giải:

Từ mỗi đỉnh của tam giác, ta kẻ được 1 đường phân giác của tam giác nên mỗi tam giác có 3 đường phân giác.

HĐ 3 trang 74 Toán lớp 7: Cắt một tam giác bằng giấy. Hãy gấp tam giác vừa cắt để được ba đường phân giác của nó. Mở tờ giấy ra, hãy quan sát và cho biết ba nếp gấp đó có cùng đi qua một điểm không (H.9.33)

HĐ 3 trang 74 Toán lớp 7 Tập 2 | Kết nối tri thức (ảnh 2)

Phương pháp giải:

Gấp theo hướng dẫn

Lời giải:

Ba nếp gấp đi qua cùng một điểm.

Giải Toán 7 trang 75 Tập 2

Luyện tập 2 trang 75 Toán lớp 7: Cho tam giác ABC có hai đường phân giác AM, BN cắt nhau tại điểm I. Hỏi CI có là đường phân giác của góc C không?

Phương pháp giải:

Sử dụng định lí về sự đồng quy của ba đường phân giác của tam giác.

Lời giải:

Xét tam giác ABC có 2 đường phân giác của tam giác cắt nhau điểm I nên đường phân giác còn lại của tam giác cũng đi qua điểm I ( tính chất đồng quy của 3 đường phân giác)

Vậy CI có là đường phân giác của góc C.

Vận dụng 2 trang 75 Toán lớp 7: Chứng minh rằng trong tam giác đều, điểm cách đều 3 cạnh của tam giác là trọng tâm của tam giác đó.

Phương pháp giải:

Sử dụng tính chất trong tam giác cân.

Lời giải:

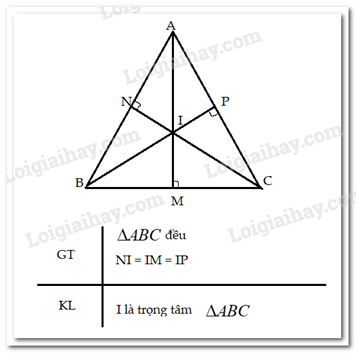
Vận dụng 2 trang 75 Toán lớp 7 Tập 2 | Kết nối tri thức (ảnh 1)

Vì $Δ A B C$ đều nên AB = AC = BC (tính chất tam giác đều)

Vì I là điểm cách đều 3 cạnh của tam giác nên là giao điểm của 3 đường phân giác của tam giác ABC

Áp dụng ví dụ 2, ta được, AI là đường trung tuyến của $Δ A B C$

Tương tự, ta cũng được BI, CI là đường trung tuyến của $Δ A B C$

Vậy I là giao điểm của ba đường đường trung tuyến của $Δ A B C$ nên I là trọng tâm của $Δ A B C$ .

Chú ý:

Với tam giác đều, giao điểm của 3 đường trung tuyến cũng là giao điểm của 3 đường phân giác.

Giải Toán 7 trang 76 Tập 2

Bài tập

Bài 9.20 trang 76 Toán lớp 7: Cho tam giác ABC với hai đường trung tuyến BN, CP và trọng tâm G. Hãy tìm số thích hợp vào chỗ chấm hỏi để được các đẳng thức

BG = ? BN, CG = ? CP;

BG = ? GN, CG = ? GP.

Phương pháp giải:

+) Sử dụng định lí về sự đồng quy của ba đường trung tuyến của tam giác.

+) Quy tắc cộng đoạn thẳng.

Lời giải:

Bài 9.20 trang 76 Toán lớp 7 Tập 2 | Kết nối tri thức (ảnh 1) Vì G là trọng tâm của $Δ A B C$ nên $B G = \frac{2}{3} B N, C G = \frac{2}{3} C P$

Ta có: GN = BN – BG = BN – $\frac{2}{3}$ BN = $\frac{1}{3}$ BN; GP = CP – CG = CP – $\frac{2}{3}$ CP = $\frac{1}{3}$ CP

Do đó, BN = 3. GN ; CP = 3. GP

Như vậy, $B G = \frac{2}{3} B N = \frac{2}{3} .3 . G N = 2 G N; C G = \frac{2}{3} C P = \frac{2}{3} .3 . G P = 2 G P$

Vậy $B G = \frac{2}{3} B N, C G = \frac{2}{3} C P$ ;

BG = 2GN; CG = 2GP.

Bài 9.21 trang 76 Toán lớp 7: Chứng minh rằng:

a) Trong một tam giác cân, hai đường trung tuyến ứng với 2 cạnh bên là hai đoạn thẳng bằng nhau.

b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Phương pháp giải:

Xét các tam giác bằng nhau, suy ra cặp cạnh tương ứng bằng nhau.

Lời giải:

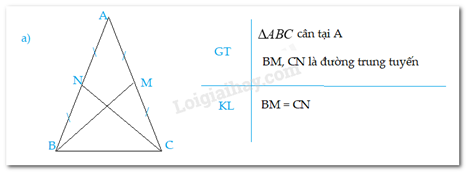
Bài 9.21 trang 76 Toán lớp 7 Tập 2 | Kết nối tri thức (ảnh 1)

Gọi BM, CN là 2 đường trung tuyến của $Δ A B C$

$\Rightarrow$ MA = MC = $\frac{1}{2}$ AC; NA = NB = $\frac{1}{2}$ AB

Vì $Δ A B C$ cân tại A nên AB = AC ( tính chất)

Do đó, AM = MC = NA = NB

Xét $Δ$ ANC và $Δ$ AMB, ta có:

AN = AM

$\hat{A}$ chung

AC = AB

$\Rightarrow$ $Δ$ ANC = $Δ$ AMB (c.g.c)

$\Rightarrow$ NC = MB ( 2 cạnh tương ứng)

Vậy 2 đường trung tuyến ứng với 2 cạnh bên của tam giác cân là hai đoạn thẳng bằng nhau.

Vì $∆ A B C$ có hai đường trung tuyến $B M$ và $C N$ cắt nhau ở $G$

$\Rightarrow$ $G$ là trọng tâm của tam giác $A B C$ .

$\Rightarrow G B = \frac{2}{3} B M$ ; $G C = \frac{2}{3} C N$ ( tính chất đường trung tuyến trong tam giác)

Mà $B M = C N$ (giả thiết) nên $G B = G C .$

Tam giác $G B C$ có $G B = G C$ nên $∆ G B C$ cân tại $G$ .

$\Rightarrow$ $\hat{G C B} = \hat{G B C}$ (Tính chất tam giác cân).

Xét $∆ B C N$ và $∆ C B M$ có:

+) $B C$ là cạnh chung

+) $C N = B M$ (giả thiết)

+) $\hat{G C B} = \hat{G B C}$ (chứng minh trên)

Suy ra $∆ B C N = ∆ C B M$ (c.g.c)

$\Rightarrow$ $\hat{N B C} = \hat{M C B}$ (hai góc tương ứng).

$\Rightarrow ∆ A B C$ cân tại $A$ (tam giác có hai góc bằng nhau là tam giác cân)

Bài 9.22 trang 76 Toán lớp 7: Cho góc xOy khác góc bẹt. Dùng compa dựng đường tròn tâm O cắt Ox tại A và cắt Oy tại B. Sau đó dựng hai đường tròn tâm A, tâm B có bán kính bằng nhau sao cho chúng cắt nhau tại M nằm nên trong góc xOy. Chứng minh rằng tia OM là tia phân giác của góc xOy.

Phương pháp giải:

Xét các tam giác bằng nhau, suy ra cặp góc tương ứng bằng nhau.

Lời giải:

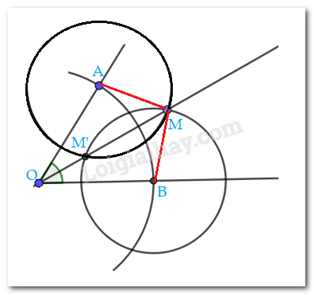
Bài 9.22 trang 76 Toán lớp 7 Tập 2 | Kết nối tri thức (ảnh 1)

Ta có: AM = bán kính đường tròn tâm A

BM = bán kính đường tròn tâm B

Mà 2 đường tròn này có bán kính bằng nhau

Do đó, AM = BM

Xét $Δ$ OAM và $Δ$ ONM có:

OA = OB( = bán kính đường tròn tâm O)

MA = MB

OM chung

$\Rightarrow$ $Δ$ OAM và $Δ$ ONM ( c.c.c)

$\Rightarrow$ $\hat{A O M} = \hat{B O M}$ ( 2 góc tương ứng)

Mà OM nằm giữa 2 tia OA và OB

$\Rightarrow$ OM là tia phân giác của góc AOB.

Bài 9.23 trang 76 Toán lớp 7: Kí hiệu I là điểm đồng quy của ba đường phân giác trong tam giác ABC. Tính góc BIC khi biết góc BAC bằng 120 $^{\circ}$ .

Phương pháp giải:

Áp dụng tính chất tia phân giác của một góc và tổng 3 góc trong một tam giác bằng 180 độ.

Lời giải:

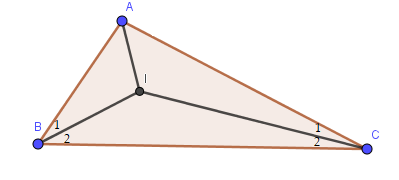
Bài 9.23 trang 76 Toán lớp 7 Tập 2 | Kết nối tri thức (ảnh 1)

Vì BI là tia phân giác của góc ABC nên $\hat{B_{1}} = \hat{B_{2}} = \frac{1}{2} . \hat{A B C}$

Vì CI là tia phân giác của góc ACB nên $\hat{C_{1}} = \hat{C_{2}} = \frac{1}{2} . \hat{A C B}$

Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:

$\begin{array}{l} \hat{B A C} + \hat{A B C} + \hat{A C B} = 180^{\circ} \\ \Rightarrow \hat{A B C} + \hat{A C B} = 180^{\circ} - \hat{B A C} = 180^{\circ} - 120^{\circ} = 60^{\circ} \\ \Rightarrow \hat{B_{2}} + \hat{C_{2}} = \frac{1}{2} . (\hat{A B C} + \hat{A C B}) = \frac{1}{2} {.60}^{\circ} = 30^{\circ} \end{array}$

Áp dụng định lí tổng ba góc trong tam giác BIC, ta có:

$\begin{array}{l} \hat{B I C} + \hat{B_{2}} + \hat{C_{2}} = 180^{\circ} \\ \Rightarrow \hat{B I C} = 180^{\circ} - (\hat{B_{2}} + \hat{C_{2}}) = 180^{\circ} - 30^{\circ} = 150^{\circ} \end{array}$

Vậy $\hat{B I C} = 150^{\circ}$

Bài 9.24 trang 76 Toán lớp 7: Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh BE = CF.

Phương pháp giải:

Sử dụng tính chất của tam giác cân, xét 2 tam giác bằng nhau rồi chỉ ra 2 cạnh tương ứng bằng nhau.

Lời giải:

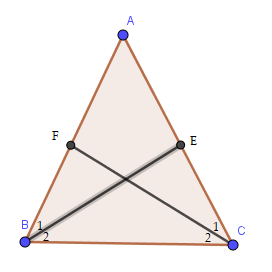
Bài 9.24 trang 76 Toán lớp 7 Tập 2 | Kết nối tri thức (ảnh 1)

Vì tam giác ABC cân tại A nên AB = AC; $\hat{A B C} = \hat{A C B}$ ( tính chất)

Vì BE là là tia phân giác của góc ABC nên $\hat{B_{1}} = \hat{B_{2}} = \frac{1}{2} . \hat{A B C}$

Vì CF là tia phân giác của góc ACB nên $\hat{C_{1}} = \hat{C_{2}} = \frac{1}{2} . \hat{A C B}$

Do đó, $\hat{B_{1}} = \hat{C_{1}}$

Xét $Δ A B E$ và $Δ A C F$ , ta có:

$\hat{A}$ chung

AB = AC

$\hat{B_{1}} = \hat{C_{1}}$

$\Rightarrow Δ A B E = Δ A C F (g . c . g)$

$\Rightarrow$ BE = CF ( 2 cạnh tương ứng)

Bài 9.25 trang 76 Toán lớp 7: Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB.

a) Hãy giải thích tại sao DP = DR.

b) Hãy giải thích tại sao DP = DQ.

c) Từ câu a và b suy ra DR = DQ. Tại sao D nằm trên tia phân giác của góc A? ( Đây là một cách chứng minh định lí 2)

Phương pháp giải:

Sử dụng tính chất tia phân giác của một góc, xét 2 tam giác bằng nhau, suy ra các cạnh tương ứng bằng nhau.

Lời giải:

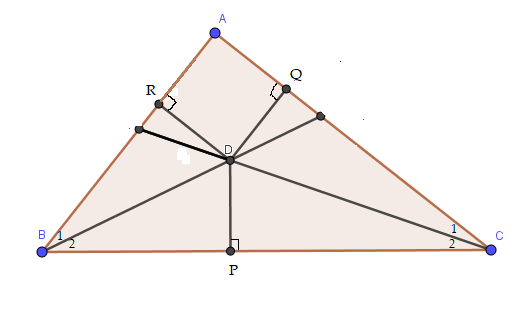
Bài 9.25 trang 76 Toán lớp 7 Tập 2 | Kết nối tri thức (ảnh 1)

a) Vì BD là tia phân giác của góc ABC nên $\hat{B_{1}} = \hat{B_{2}} = \frac{1}{2} . \hat{A B C}$

Vì CD là tia phân giác của góc ACB nên $\hat{C_{1}} = \hat{C_{2}} = \frac{1}{2} . \hat{A C B}$

Xét $Δ B D P$ vuông tại P và $Δ B D R$ vuông tại R, ta có:

$\hat{B_{2}} = \hat{B_{1}}$

BD chung

$\Rightarrow Δ B D P = Δ B D R$ ( cạnh huyền – góc nhọn)

$\Rightarrow$ DP = DR ( 2 cạnh tương ứng) (1)

b) Xét $Δ C D P$ vuông tại P và $Δ C D Q$ vuông tại Q, ta có:

$\hat{C_{2}} = \hat{C_{1}}$

CD chung

$\Rightarrow Δ C D P = Δ C D Q$ ( cạnh huyền – góc nhọn)

$\Rightarrow$ DP = DQ ( 2 cạnh tương ứng) (2)

c) Từ (1) và (2), ta được: DR = DQ ( cùng bằng DP).

D nằm trên tia phân giác của góc A do D cách đều AB và AC.

Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung trang 70

Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

Luyện tập chung trang 82

Bài tập cuối chương 9

====== ****&**** =====

Bài liên quan:

Leave a Comment Hủy