Giải bài tập Toán lớp 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
Giải Toán 7 trang 77 Tập 2
1. Sự đồng quy của ba đường trung trực trong một tam giác
Câu hỏi trang 77 Toán lớp 7: Mỗi tam giác có mấy đường trung trực
Phương pháp giải:
Đường trung trực của đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.
Lời giải:
Mỗi tam giác có 3 đường trung trực.
Giải Toán 7 trang 78 Tập 2
HĐ 1 trang 78 Toán lớp 7: Vẽ tam giác ABC ( không tù) và ba đường trung trực của các đoạn BC, CA, AB. Quan sát hình và cho biết ba đường trung trực đó có cùng đi qua một điểm hay không?
Phương pháp giải:
Đường trung trực của đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.
Lời giải:

Ba đường trung trực DP, DQ, DR cùng cắt nhau tại điểm D.
HĐ 2 trang 78 Toán lớp 7: Dùng tính chất đường trung trực của một đoạn thẳng, hãy lập luận để suy ra tính chất nói ở HĐ1 bằng cách trả lời các câu hỏi sau:
Cho O là giao điểm các đường trung trực của hai cạnh BC và CA (H.9.38)
a) Tại sao OB = OC, OC = OA.
b) Điểm O có nằm trên đường trung trực của AB không?
Phương pháp giải:
Gọi M là trung điểm BC, N là trung điểm AC
a) Chứng minh (c – g – c), (c – g – c)
b) Điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đấy.
Lời giải:

a)
Gọi M là trung điểm của BC, N là trung điểm AC.
Xét và có:
BM = CM (gt)
OM chung
(cạnh tương ứng)
Chứng minh tương tự: (c – g – c) (cạnh tương ứng)
b) Ta có:
cách đều hai đầu mút của đoạn thẳng AB
nằm trên đường trung trực của đoạn thẳng AB (tính chất đường trung trực của đoạn thẳng)
Giải Toán 7 trang 79 Tập 2
Luyện tập 1 trang 79 Toán lớp 7: Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều 3 đỉnh của tam giác đó.
Phương pháp giải:
Áp dụng: Trong tam giác cân ABC cân tại A, đường trung tuyến BN cũng là đường trung trực của AC
Từ đó chứng minh G là giao điểm ba đường trung trực của tam giác ABC
Lời giải:

Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại B có BN là đường trung tuyến
là đường trung trực của đoạn thẳng AC
Tam giác BAC cân tại A có AP là đường trung tuyến
là đường trung trực của đoạn thẳng BC
Mà
là giao điểm ba đường trung trực của tam giác ABC
.
Vận dụng 1 trang 79 Toán lớp 7: Em hãy trả lời câu hỏi trong tình huống mở đầu.
Phương pháp giải:
Địa điểm khoan giếng cách đều 3 ngôi nhà
Lời giải:
3 ngôi nhà không thẳng hàng nên tạo thành 1 tam giác, ta gọi là tam giác ABC.
Điểm khoan giếng cách đều 3 ngôi nhà khi và chỉ khi điểm khoan giếng là giao điểm của 3 đường trung trực của tam giác ABC.
Vậy, ta cần vẽ 2 đường trung trực của tam giác ABC, chúng cắt nhau tại đâu thì đó là điểm cần khoan giếng.
Thử thách nhỏ trang 79 Toán lớp 7: Sử dụng tính chất đường trung trực của một đoạn thẳng, hãy giải thích nếu điểm Q cách đều 3 đỉnh của tam giác ABC thì Q phải là giao điểm ba đường trung trực của tam giác ABC.
Phương pháp giải:
Điểm cách đều 2 mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng.
Lời giải:
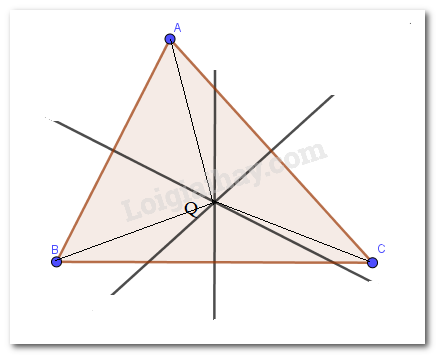
Vì Q cách đều 3 đỉnh của tam giác ABC nên GA=GB=GC
Vì QA=QB nên Q nằm trên đường trung trực của đoạn thẳng AB (tính chất đường trung trực của đoạn thẳng).
Vì QA=QC nên Q nằm trên đường trung trực của đoạn thẳng AC (tính chất đường trung trực của đoạn thẳng).
Vì QB=QC nên Q nằm trên đường trung trực của đoạn thẳng BC (tính chất đường trung trực của đoạn thẳng).
Vậy Q là giao điểm của 3 đường trung trực của tam giác ABC.
2. Sự đồng quy của ba đường cao trong một tam giác
Câu hỏi trang 79 Toán lớp 7: Mỗi tam giác có mấy đường cao?
Phương pháp giải:
Đường cao là đoạn thẳng đi qua đỉnh và vuông góc với cạnh đối diện.
Lời giải:
Ứng với 1 cạnh của tam giác, ta có 1 đường cao
Vậy mỗi tam giác có 3 đường cao.
HĐ 3 trang 79 Toán lớp 7: Vẽ tam giác ABC và 3 đường cao của nó. Quan sát hình và cho biết, ba đường cao đó có cùng đi qua một điểm hay không ?
Phương pháp giải:
Đường cao của một tam giác là đoạn thẳng kẻ từ một đỉnh và vuông góc với cạnh đối diện
Lời giải:
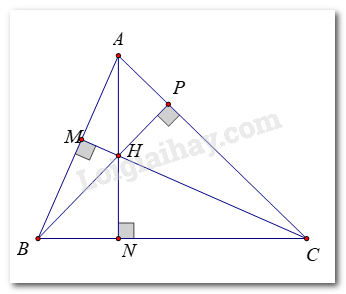
Ba đường cao AN, BP, CM cùng đi qua điểm H.
Giải Toán 7 trang 81 Tập 2
Luyện tập 2 trang 81 Toán lớp 7: a) Chứng minh trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
Phương pháp giải:
a) Chứng minh A thuộc đường trung trực BC nên AD là đường cao.
Chứng minh: từ đó suy ra AD là phân giác góc A
b) Điểm cách đều ba đỉnh là giao của ba đường trung trực trong tam giác GA = GB = GC
Sử dụng kết quả ý a, chứng minh G là giao điểm ba đường phân giác trong tam giác ABC
Lời giải:
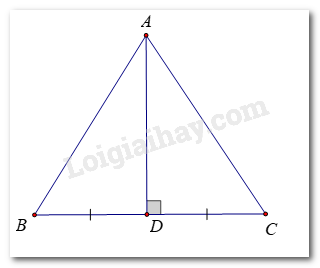
a) Kẻ đường trung trực của đoạn thẳng BC, cắt BC tại D
Ta có: Tam giác ABC cân nên AB = AC
thuộc đường trung trực của cạnh BC (t/c)
là đường trung trực của BC.
Xét và có:
AB = AC (gt)
BD = CD (gt)
AD: cạnh chung
AD là tia phân giác góc BAC.
Vậy tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b)
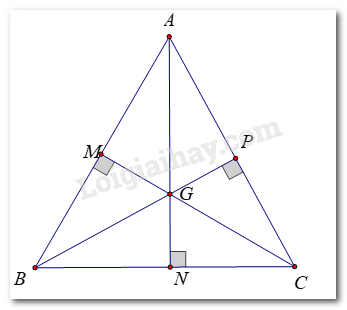
Ta có: Điểm cách đều ba đỉnh của tam giác là giao điểm ba đường trung trực của tam giác đó.
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại A có AN là đường trung tuyến
AN là đường phân giác xuất phát từ đỉnh A (cm ở ý a)
Tương tự: BP, CM lần lượt là đường phân giác xuất phát từ B và C của tam giác ABC
Mà AN cắt BP tại G
là giao điểm ba đường phân giác của tam giác ABC
cách đều ba cạnh của tam giác ABC (Tính chất)
Bài tập
Bài 9.26 trang 81 Toán lớp 7: Gọi H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HBC, HCA, HAB.
Phương pháp giải:
-Trực tâm của tam giác là giao điểm của ba đường cao
-Xác định các đường cao của mỗi tam giác.
Lời giải:
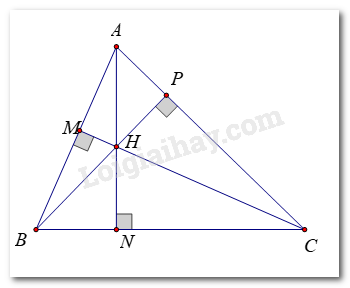
a)
Trong ΔABC ta có H là trực tâm nên:
AH ⊥ BC tại N, BH ⊥ AC tại P, CH ⊥ AB tại M
Trong ΔAHB, ta có:
HM ⊥ AB
BN ⊥ AH
Mà MH cắt BN tại C
=> C là trực tâm của tam giác AHB.
Trong ΔHAC, ta có:
HP ⊥ AC
CN ⊥ AH
Mà HP cắt CN tại B
=> B là trực tâm của ΔHAC.
Trong ΔHBC, ta có:
HN ⊥ BC
BM ⊥ HC
Mà HN cắt BM tại A
=> A là trực tâm của tam giác HBC
Bài 9.27 trang 81 Toán lớp 7: Cho tam giác ABC có và trực tâm H. Tìm góc BHC.
Phương pháp giải:
– Tính (Kề bù )
– Tính (Tam giác ABD vuông tại D)
– Tính (Tam giác BHE vuông tại E)
Lời giải:
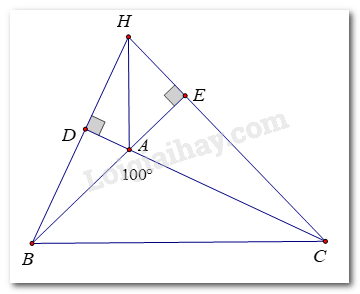
Gọi E là chân đường cao từ C xuống AB, D là chân đường cao từ B xuống AC
=> HC ⊥ BE, HB ⊥ CD
Ta có:
∆ ADB là tam giác vuông tại D:
∆ BEH là tam giác vuông tại E
Hay
Bài 9.28 trang 81 Toán lớp 7: Xét điểm O cách đều 3 đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.
Phương pháp giải:
Chứng minh tam giác ABC có một góc bằng 90 độ
Lời giải:
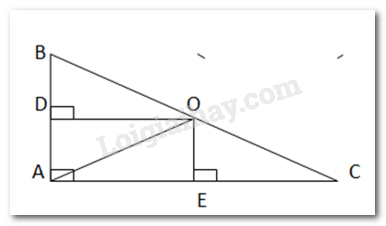
O cách đều 3 đỉnh của tam giác ABC
cân tại O.
Giả sử O là trung điểm BC
cân tại O
Xét tam giác ABC có
Vậy nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.
Bài 9.29 trang 81 Toán lớp 7: a) Có một chi tiết máy ( đường viền ngoài là đường tròn) bị gãy. (H.9.46). Làm thế nào để xác định được bán kính của đường viền này ?
b) Trên bản đồ, ba khu dân cư được quy hoạch tại điểm A, B, C không thẳng hàng. Hãy tìm trên bản đồ một điểm M cách đều A, B, C để quy hoạch một trường học

Phương pháp giải:
a) Lấy ba điểm phân biệt A, B, C trên đường viền ngoài chi tiết máy sau đó xác định giao điểm 3 đường trung trực của đoạn AB, BC, CA.
b) Vẽ đường trung trực của các đoạn AB, AC, BC.
Lời giải:
a)

– Lấy ba điểm phân biệt A, B, C trên đường viền ngoài chi tiết máy.
– Vẽ đường trung trực cạnh AB và cạnh BC. Hai đường trung trực này cắt nhau tại O. Khi đó O là tâm cần xác định.
– Bán kính đường tròn cần tìm là độ dài đoạn OB (hoặc OA hoặc OC).
b)
– Bước 1: Vẽ đường trung trực của các đoạn AB, AC, BC
– Bước 2: 3 đường trung trực này cắt nhau tại M. Khi đó MA= MB=MC.
– Bước 3: M là điểm cần xác định.
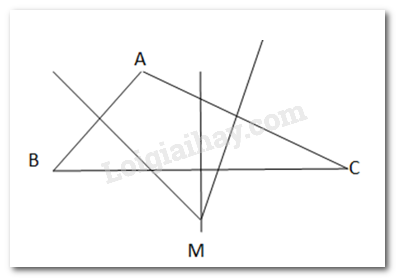
Bài 9.30 trang 81 Toán lớp 7: Cho hai đường thẳng không vuông góc b,c cắt nhau tại điểm A và cho điểm H không thuộc b và c (H.9.47). Hãy tìm điểm B thuộc b, điểm C thuộc c sao cho tam giác ABC nhận H làm trực tâm.
Phương pháp giải:
Để vẽ trực tâm ta xác định 2 đường cao của tam giác trên. Giao điểm của 2 đường cao chính là trực tâm của tam giác.
Lời giải:
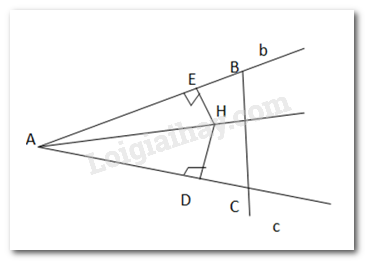
– Kẻ HD đường thẳng c tại điểm D, HE đường thẳng b tại điểm E
– Nối A với H. Kéo dài DH cắt đường thẳng b tại B.
Từ B kẻ đường vuông góc với AH, đường thẳng đó cắt đường thẳng c tại 1 điểm. Điểm đó chính là điểm C.
=> H là trực tâm của tam giác ABC.
Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Luyện tập chung trang 70
Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
Luyện tập chung trang 82
Bài tập cuối chương 9
====== ****&**** =====