Mời các quý thầy cô cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Tiết 3: LUYỆN TẬP
I. MỤC TIÊU:
1. Về kiến thức:
– Củng cố được cách tìm điều kiện xác định (hay điều kiện có nghĩa) của và có kĩ năng thực hiện điều đó khi biểu thức A không phức tạp
– Biết vận dụng hằng đẳng thức = |A| để rút gọn biểu thức
2. Về năng lực:
– Giúp học sinh phát huy năng lực tính toán, năng lực giải quyết vấn đề, năng lực hợp tác, năng lực ngôn ngữ, năng lực tự học.
3. Về phẩm chất: Phẩm chất: Tự tin, tự chủ.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU.
1. Giáo viên: Phấn mầu, bảng phụ.
2. Học sinh: Đồ dùng học tập, học bài và làm bài ở nhà
III. TIẾN TRÌNH DẠY HỌC
1. Hoạt động 1: Mở đầu(Khởi động)
HS 1: – Nêu điều kiện để có nghĩa.
– Chữa bài tập12(a,b)tr11,sgk.
Tìm x để mỗi căn thức sau đây có nghĩa :
a) b)
HS 2: – Điền vào chỗ trống (…) để được khẳng định đúng: = . . . = 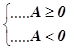
– Chữa bài tập 8(a,b), sgk
2. Hoạt động 2: Hình thành kiến thức
– Mục tiêu: Củng cố lại những kiến thức cơ bản về căn bậc hai số học, căn thức bậc hai, hằng đẳng thức
– Phương pháp: Nêu vấn đề, thuyết trình, vấn đáp, trực quan.
– Năng lực: Thuyết trình, sử dụng ngôn ngữ.
– SP: HS được tái hienj lại những kiens thức đã học, vận dụng được để làm bài tập
|
NỘI DUNG |
SẢN PHẤM |
||
|
Giáo viên giao nhiệm vụ: HĐ cá nhân – Nhắc lại các kiến thức về: + căn bậc hai số học + Căn thức bậc hai + Hằng đẳng thức. + Điều kiện để căn thức bậc hai có nghĩa |
I. Kiến thức cần nhớ:SGK |
||
|
3. Hoạt động 3: Luyện tập – : Vận dụng *Mục tiêu: Củng cố về điều kiện để một căn thức có nghĩa và hằng đẳng thức Phương pháp: Nêu vấn đề, thuyết trình, vấn đáp, trực quan |
|||
|
Giáo viên |
Học sinh |
Sản phẩm |
|
|
*Giao nhiệm vụ: Làm bài tập SGK *Cách thức hoạt động: +Giao nhiệm vụ: Hoạt động cá nhân (lên bảng trình bày bài) +Thực hiện nhiệm vụ: Gv gọi Hs lên bảng trình bày Hướng dẫn HS làm bài 12(c,d)/11 ? Điều kiện xác định của căn thức bậc hai là gì?
? Một phân số không âm mà có tử dương vậy mẫu của nó như thế nào?
? Bình phương của một số bất kì có giá trị như thế nào? – Gọi 2HS lên bảng trình bày bài 12c,d/T11 sgk
Cho HS chữa bài 9.
Đưa về giải phương trình dạng hoặc đưa về dạng
Gọi HS nhận xét bài làm của bạn
Cho HS làm bài 11(a,d) theo thứ tự thực hiện các phép tính là khai phương hay lũy thừa, nhân hay chia, tiếp đến là cộng hay trừ, từ trái sang phải.
Cho HS làm bài 13(a,c)/11 Hướng dẫn HS sử dụng hằng đẳng thức GV gọi HS lên bảng làm bài. Gọi HS nhận xét bài làm của bạn.
Cho HS làm bài 14(a,d)/11 Hướng dẫn HS sử dụng: Với a0 thì a=()2 để đưa các đa thức về dạng hằng đẳng thức để áp dụng. Bổ sung thệm: Cho HS nhắc lại các hằng đẳng thức có liên quan |
– HS nắm cách làm từ phần hỏi bài cũ và hoàn thành các BT gv yêu cầu
Bốn HS lên bảng trình bày bài làm của mình. HS dưới lớp nhận xét bài làm của các bạn
HS cả lớp làm bài vào vở, mỗi dãy lớp làm 1 câu Mỗi dãy một HS lên bảng trình bày bài làm. Các HS khác nhận xét và sửa sai
Biểu thức dưới dấu căn không âm Mẫu của phân số dương
Bình phương của một số bao giờ cũng lớn hơn hoặc bằng 0
HS làm bài vào vở theo hướng dẫn của GV sau đó hai HS lên bảng trình bày bài làm của mình. HS dưới lớp nhận xét bài làm của bạn.
– HS tiến hành hoạt động nhóm vào bảng phụ nhóm – Các nhóm báo cáo kết quả.
HS suy nghĩ làm bài cá nhân
HS: A2–B2=(A–B)(A+B) (A–B)2=A2 – 2AB+B2
Suy nghĩ làm ý e và g HS trình bày
|
* Dạng 1: Tìm điều kiện để căn thức có nghĩa: Bài 12/11: c/ Căn thức có nghĩa –1+x0 => x1 d/ Căn thức có nghĩa khi và chỉ khi 1+x2 0 mà x20 nên 1+x20 với xR
* Dạng 2:Tìm x Bài 9/11: Tìm x biết: (Áp dụng hằng đẳng thức) a/ => x1 = 7 và x2= –7 b/ x1 =8 và x2= –8 c/ x1 =3 và x2= –3
d/ x1=4và x2= –4 * Dạng 3:Tính toán, rút gọn Bài 11/11: Tính: a/ =4.5+14:7 =20+2=22
Bài 13/11: Rút gọn các bt: a/ = = –2a–5a (vì a = –7a c/ = = =6a2 (vì 3a20) Bài 14/11: Phân tích thành nhân tử a/ x2 – 3 = x2 – = d/ x2 – 2x+5 = (x – )2 |
|
|
Hướng dẫn học ở nhà – HS chủ động làm các bài tập về nhà để củng cố kiến thức đã học. – HS chuẩn bị bài mới giúp tiếp thu tri thức sẽ học trong buổi sau. |
|||
|
Bài tập về nhà: 11(b,c), 12(a,b) 13(b,d) 14(b,c), 15/11 SGK 12, 13, 14, 15/5 18/6 SBT Hướng dẫn: Bài 15 trước tiên phân tích vế trái thành nhân tử sau đó giải phương trình tích dạng A.B=0 => A=0 hoặc B=0 |
|||
RÚT KINH NGHIỆM, BỔ SUNG :
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………
Xem thêm