Giải bài tập Toán 9 Bài 3: Liên hệ giữa phép nhân và phép khai phương
Trả lời câu hỏi giữa bài
Trả lời câu hỏi 1 trang 12 SGK Toán 9 Tập 1 :Tính và so sánh: và
Phương pháp giải:
Tính toán hai biểu thức rồi so sánh kết quả với nhau.
Lời giải:
Vậy
Trả lời câu hỏi 2 trang 13 SGK Toán 9 Tập 1 :Tính
a)
b)
Phương pháp giải:
Sử dụng công thức khai phương một tích với không âm.
Lời giải:
a)
b)
Trả lời câu hỏi 3 trang 14 SGK Toán 9 Tập 1: Tính
a)
b)
Phương pháp giải:
Sử dụng công thức với không âm.
Lời giải:
a)
b)
Trả lời câu hỏi 4 trang 13 SGK Toán 9 Tập 1 :Rút gọn các biểu thức sau (với và không âm):
a) b)
Phương pháp giải:
Sử dụng các công thức sau:
+ Với không âm ta có
+
Lời giải:
a) Ta có
(do
b) Ta có (do
Bài tập ( trang 14, 15, 16 SGK Toán 9)
Bài 17 trang 14 SGK Toán 9 Tập 1 :Áp dụng quy tắc khai phương một tích, hãy tính:
a) ; b) ;
c) ; d) .
Phương pháp giải:
Sử dụng các công thức:
+) .
+) Nếu thì .
Nếu thì
+) , với .
+) , với .
Lời giải:
a) Ta có:
.
b) Ta có:
.
c) Ta có:
.
d) Ta có:
.
Bài 18 trang 14 SGK Toán 9 Tập 1 :Áp dụng quy tắc nhân các căn bậc hai, hãy tính:
a) ; b) ;
c) ; d) .
Phương pháp giải:
Sử dụng các công thức:
+) , với .
+) Với mọi số , luôn có .
+) Với mọi ta có: .
Lời giải:
a) Ta có:
.
b) Ta có:
.
c) Ta có:
.
d)
.
Bài 19 trang 15 SGK Toán 9 Tập 1: Rút gọn các biểu thức sau:
a) với ;
b) với ;
c) với ;
d) . với .
Phương pháp giải:
Sử dụng các công thức:
Sử dụng các công thức:
+), với .
+)
+) , nếu .
+) , nếu .
Lời giải:
a) Ta có:
(Vì nên .
b)
Vì ≥ 0 nên .
Vì hay nên .
.
Ta có: .
.
.
c)
Vì hay nên .
.
Ta có:
.
d)
Vì , với mọi nên .
Vì nên . Do đó .
Ta có: .
.
Bài 20 trang 15 SGK Toán 9 Tập 1: Rút gọn các biểu thức sau:
a) . với ;
b) với ;
c) với ;
d) .
Phương pháp giải:
Sử dụng các công thức sau:
+) , với .
+) Với mọi số , luôn có .
+)
Lời giải:
a) Ta có:
.
(Vì nên ).
b) Ta có:
(vì )
c)
Do nên bài toán luôn được xác định.
Ta có:
(vì nên
d) Ta có:
.
+) : Nếu .
Do đó:
.
+) : Nếu .
Do đó:
.
Vậy , nếu .
, nếu .
Bài 21 trang 15 SGK Toán 9 Tập 1: Khai phương tích được:
; ; ;
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng các công thức sau:
+) , với .
+) Nếu thì .
+) Nếu thì .
+) Với mọi ta có: .
Lời giải:
Ta có:
.
Vậy đáp án đúng là
Bài 22 trang 15 SGK Toán 9 Tập 1: Biến đổi các biểu thức dưới dấu căn thành dạng tích rồi tính:
a) ; b) ;
c) ; d) .
Phương pháp giải:
Sử dụng các công thức sau:
+) .
+) , với .
+) .
+) Nếu thì
Nếu thì
Lời giải:
a) Ta có
.
b) Ta có:
.
.
c) Ta có:
.
d) Ta có:
.
Bài 23 trang 15 SGK Toán 9 Tập 1: Chứng minh.
a) ;
b) và là hai số nghịch đảo của nhau.
Phương pháp giải:
Sử dụng các công thức sau:
+) .
+) , với .
+) Muốn chứng minh hai số là nghịch đảo của nhau ta chứng minh tích của chúng bằng .
Lời giải:
a) Ta có:
b)
Ta tìm tích của hai số và
Ta có:
=
Do đó
Vậy hai số trên là nghịch đảo của nhau.
Bài 24 trang 15 SGK Toán 9 Tập 1:Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ ) của các căn thức sau:
tại ;
tại .
Phương pháp giải:
Sử dụng các công thức sau:
+) .
+) .
+) , với .
+) .
+) Nếu thì .
Nếu thì .
+) , với .
Lời giải:
a) Ta có:
.
(Vì với mọi nên )
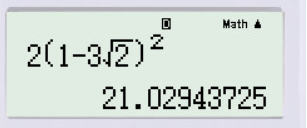
Thay vào biểu thức rút gọn trên, ta được:
.
Bấm máy tính, ta được: .
b) Ta có:
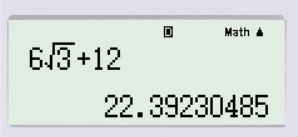
Thay và vào biểu thức rút gọn trên, ta được:
.
Bấm máy tính, ta được: .
Bài 25 trang 16 SGK Toán 9 Tập 1: Tìm biết:
a) ; b) ;
c) ; d) .
Phương pháp giải:
– Đặt điều kiện để biểu thức có nghĩa: có nghĩa khi và chỉ khi
– Bình phương hai vế rồi giải bài toán tìm x.
– Ta sử dụng các cách làm sau:
Lời giải:
a) Điều kiện:
(thỏa mãn điều kiện)
Vậy .
Cách khác:
b) Điều kiện:
(thỏa mãn điều kiện)
Vậy .
c) Điều kiện:
(thỏa mãn điều kiện)
Vậy .
Cách khác:
d) Điều kiện: (vì với mọi
Vậy
Bài 26 trang 16 SGK Toán 9 Tập 1: a) So sánh và ;
b) Với và , chứng minh .
Phương pháp giải:
+) Sử dụng định lí so sánh hai căn bậc hai:
, với .
+) Sử dụng các công thức: với , ta có:
.
.
Lời giải:
a) Ta có:
.
.
Vì nên
Vậy
b) Với , ta có
.
.
Vì nên
(đpcm)
Bài 27 trang 16 SGK Toán 9 Tập 1: So sánh
a) và ; b) và
Phương pháp giải:
+) Sử dụng các công thức sau: , với .
+) Sử dụng định lí so sánh hai căn bậc hai số học:
, với .
+) Sử dụng tính chất của bất đẳng thức:
, với .
Lời giải:
a) Ta có:
Cách khác:
Ta có:
Vì
Hay .
b) Vì
(Nhân cả hai vế bất phương trình trên với )
Vậy .
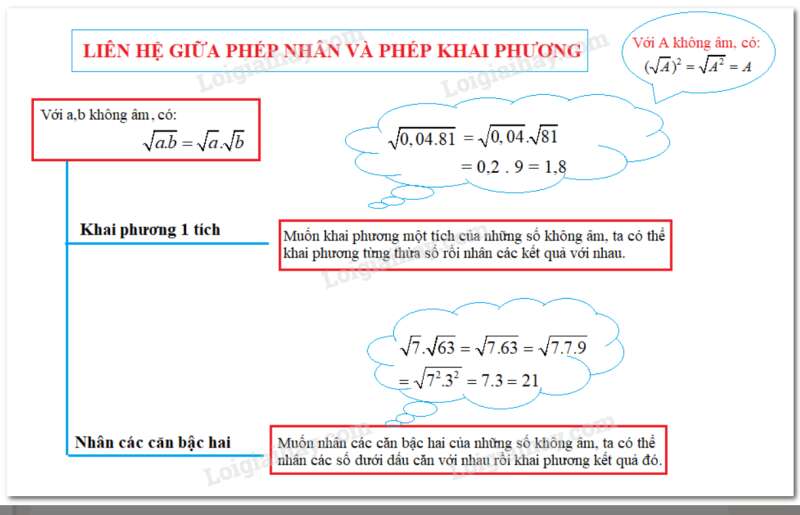
Lý thuyết Bài 3: Liên hệ giữa phép nhân và phép khai phương
1. Định lí
Với các số và không âm ta có:
Lưu ý:
+) Với hai biểu thức không âm A và B, ta cũng có:
+) Nếu không có điều kiện A và B không âm thì không thể viết đẳng thức trên.
Chẳng hạn được xác định nhưng đẳng thức không xác định.
2. Áp dụng
a. Quy tắc khai phương một tích
Muốn khai phương một tích của những số không âm, ta có thể khai phương từng thừa số rồi nhân các kết quả với nhau.
+ Mở rộng: Với các số không âm ta có:
b. Quy tắc nhân các căn bậc hai
Muốn nhân các căn bậc hai của những số không âm, ta có thể nhân các số dưới dấu căn với nhau rồi khai phương kết quả đó.
+ Mở rộng: Với các số không âm ta có: .
+ Với biểu thức không âm, ta có:
3. Dạng toán cơ bản
Dạng 1: Thực hiện phép tính
Sử dụng: Với hai biểu thức không âm A và B, ta có:
Ví dụ:
Dạng 2: Rút gọn biểu thức
Sử dụng: Với hai biểu thức không âm A và B, ta có:
Ví dụ: