Giải SBT Toán 9 Bài 5: Bảng căn bậc hai
Bài 47 trang 13 SBT Toán 9 tập 1: Dùng bảng căn bậc hai tìm , biết:
a) ;
b) ;
c) ;
d)
Phương pháp giải:
Sử dụng suy ra hoặc (với ).
Sử dụng bảng căn bậc hai.
Lời giải:
a)
Dùng bảng căn bậc hai ta có:
b)
c)
d)
Bài 48 trang 13 SBT Toán 9 tập 1: Dùng bảng bình phương tìm , biết:
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
Dùng bảng bình phương để tìm
ÁP dụng: Với
.
Lời giải:
a)
b)
c)
;
d)
.
Bài 49 trang 13 SBT Toán 9 tập 1: Kiểm tra kết quả bài 47, 48 bằng máy tính bỏ túi.
Phương pháp giải:
Sử dụng máy tính bỏ túi để kiểm tra kết quá
Lời giải:
Ví dụ: Với câu a) bài 47, ta có:
Tương tự với các câu tiếp theo.
Bài 50 trang 13 SBT Toán 9 tập 1: Thử lại kết quả bài 47 bằng bảng bình phương.
Phương pháp giải:
Sử dụng bảng bình phương.
Lời giải:
Với câu a) bài 47 ta có
Tìm ô có giá trị gần với 15 trong bảng bình phương ta được ô 14,98 và ô 15,05
* Với ô 14,98 tra bảng ta được . Đây là kết quả gần đúng nhưng hơi thiếu.
* Với ô 15,05 tra bảng ta được . Đây là kết quả gần đúng nhưng hơi thừa.
Thực hiện tương tự cho các bài còn lại.
Bài 51 trang 13 SBT Toán 9 tập 1: Thử lại kết quả bài 48 bằng bảng căn bậc hai.
Phương pháp giải:
Sử dụng bảng căn bậc hai.
Lời giải:
Sử dụng bảng căn bậc hai, thử lại các kết quả bằng cách tra bảng căn bậc hai cho các kết quả vừa tìm được ở bài 48.
Bài 52 trang 13 SBT Toán 9 tập 1: Điền vào các chỗ trống (…) trong phép chứng minh sau:
Số là số vô tỉ.
Giả sử không phải là số vô tỉ thì phải tồn tại các số nguyên m và n sao cho trong đó còn hai số và không có ước chung nào khác 1 và (hai số và nguyên tố cùng nhau).
Khi đó, ta có: … hay (1).
Kết quả (1) chứng tỏ là số chẵn, nghĩa là với là số nguyên.
Thay vào (1) ta được: … hay (2)
Kết quả (2) chứng tỏ phải là số chẵn.
Hai số và đều là số chẵn, trái với giả thiết và không có ước chung nào khác và .
Vậy là số vô tỉ.
Phương pháp giải:
Áp dụng: Với
.
Lời giải:
Số là số vô tỉ.
Giả sử không phải là số vô tỉ thì phải tồn tại các số nguyên m và n sao cho trong đó còn hai số và không có ước chung nào khác 1 và (hai số và nguyên tố cùng nhau).
Khi đó, ta có: hay (1).
Kết quả (1) chứng tỏ là số chẵn, nghĩa là với là số nguyên.
Thay vào (1) ta được: hay (2)
Kết quả (2) chứng tỏ phải là số chẵn.
Hai số và đều là số chẵn, trái với giả thiết và không có ước chung nào khác và .
Vậy là số vô tỉ.
Bài 53 trang 13 SBT Toán 9 tập 1: Chứng minh:
a) Số là số vô tỉ;
b) Các số ; đều là số vô tỉ.
Lời giải:
a)
Giả sử không phải là số vô tỉ. Khi đó tồn tại các số nguyên và sao cho với . Hai số và không có ước chung nào khác và .
Ta có: hay (1)
Kết quả trên chứng tỏ chia hết cho , nghĩa là ta có với là số nguyên.
Thay vào (1) ta được: hay
Kết quả trên chứng tỏ chia hết cho .
Hai số a và b đều chia hết cho 3, trái với giả thiết và không có ước chung nào khác và .
Vậy là số vô tỉ.
b)
Giả sử là số hữu tỉ, nghĩa là tồn tại số hữu tỉ sao cho
Suy ra: hay là số hữu tỉ.
Điều này vô lí vì là số vô tỉ (theo bài 52 trang 13 SBT toán 9 tập 1)
Vậy là số vô tỉ.
*Giả sử là số hữu tỉ, nghĩa là tồn tại một số hữu tỉ mà:
Suy ra: hay là số hữu tỉ.
Điều này vô lí vì là số vô tỉ (theo bài 52 trang 13 SBT toán 9 tập 1)
Vậy là số vô tỉ.
Bài 54 trang 14 SBT Toán 9 tập 1: Tìm tập hợp các số thỏa mãn bất đẳng thức: và biểu diễn tập hợp đó trên trục số.
Phương pháp giải:
Áp dụng: Với ta có:
.
Lời giải:
Điều kiện:
Ta có: .
Biểu diễn trên trục số:

Bài 55 trang 14 SBT Toán 9 tập 1: Tìm tập hợp các số thỏa mãn bất đẳng thức:
và biểu diễn tập hợp đó trên trục số.
Phương pháp giải:
Áp dụng:
Lời giải:
Điều kiện:
Ta có:
Suy ra
Biểu diễn trên trục số:
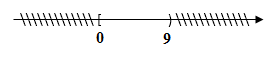
Bài tập bổ sung (trang 14 SBT Toán 9):
Bài 5.1 trang 14 SBT Toán 9 tập 1: Tra bảng căn bậc hai, tìm được . Vậy suy ra có giá trị gần đúng là:
(A)
(B)
(C)
(D)
Phương pháp giải:
Sử dụng bảng tra căn bậc hai.
Hoặc sử dụng: với
Lời giải:
Ta có:
Cách khác: Tra bảng căn bậc hai ta có:
Chọn đáp án (A).