Giải bài tập Toán 9 Bài 1: Căn bậc hai
Trả lời câu hỏi giữa bài
Trả lời câu hỏi 1 trang 4 SGK Toán 9 Tập 1:Tìm các căn bậc hai của mỗi số sau:
a) 9; b) ; c) 0,25; d) 2.
Phương pháp giải:
+ Căn bậc hai của một số a không âm là số x sao cho
+ Số dương a có đúng hai căn bậc hai là hai số đối nhau là và .
Lời giải:
+ Căn bậc hai của số là và (vì và )
+ Căn bậc hai của số là và (vì và )
+ Căn bậc hai của số là và ( vì và )
+ Căn bậc hai của số là và (vì và )
Trả lời câu hỏi 2 trang 5 SGK Toán 9 Tập 1: Tìm căn bậc hai số học của mỗi số sau:
a) 49
b) 64
c) 81
d) 1.21
Phương pháp giải:
Ta sử dụng: Nếu thì
Lời giải:
a) vì và 72 = 49
b) vì và 82 = 64
c) vì và 92 = 81
d) vì và 1,12 = 1,21
Trả lời câu hỏi 3 trang 5 SGK Toán 9 Tập 1: Tìm các căn bậc hai của mỗi số sau:
a)
b) 81
c) 1.21
Phương pháp giải:
Căn bậc hai của số không âm là và
Lời giải:
a) Căn bậc hai của số là và
b) Căn bậc hai của số là và
c) Căn bậc hai của số là và
Trả lời câu hỏi 4 trang 6 SGK Toán 9 Tập 1: So sánh:
a) 4 và
b) và 3.
Phương pháp giải:
Sử dụng với hai số không âm ta có
Lời giải:
a) Vì 16 > 15 nên . Vậy 4 >
b) Vì 11 > 9 nên . Vậy > 3
Trả lời câu hỏi 5 trang 6 SGK Toán 9 Tập 1:Tìm số không âm, biết:
a)
b)
a) Phương pháp giải:
Sử dụng với hai số không âm ta có rồi kết hợp với không âm để kết luận.
Lời giải:
Kết hợp với ta có thỏa mãn đề bài.
b) Phương pháp giải:
Sử dụng với hai số không âm ta có rồi kết hợp với không âm để kết luận.
Lời giải:
Kết hợp điều kiện ta có
Bài tập ( trang 6-7 ) SGK Toán 9
Bài 1 trang 6 SGK Toán 9 Tập 1 :Tìm căn bậc hai số học của mỗi số sau rồi suy ra căn bậc hai của chúng
121; 144; 169; 225; 256; 324; 361; 400.
Phương pháp giải:
+) Căn bậc hai số học của là với .
+) Số dương có đúng hai căn bậc hai là hai số đối nhau: Số dương kí hiệu là và số âm kí hiệu là .
Lời giải:
Ta có:
+ có căn bậc hai số học là (vì và )
có hai căn bậc hai là và .
+ có căn bậc hai số học là (vì và )
có hai căn bậc hai là và .
+ có căn bậc hai số học là (vì và )
có hai căn bậc hai là và .
+ có căn bậc hai số học là (vì và )
có hai căn bậc hai là và .
+ có căn bậc hai số học là (vì và )
có hai căn bậc hai là và .
+ có căn bậc hai số học là (vì và )
có hai căn bậc hai là và .
+ có căn bậc hai số học là (vì và )
có hai căn bậc hai là và .
+ có căn bậc hai số học là (vì và )
có hai căn bậc hai là và .
Bài 2 trang 6 SGK Toán 9 Tập 1: So sánh
a) và
b) và
c) và
Phương pháp giải:
+) Sử dụng định lí so sánh hai căn bậc hai số học: Với hai số và không âm ta có:
Lời giải :
a) Ta có:
Vì .
Vậy .
b) Ta có:
Vì
Vậy .
c) Ta có:
Vì .
Vậy .
Bài 3 trang 6 SGK Toán 9 Tập 1 :Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương trình sau (làm tròn đến chữ số thập phân thứ ):
a)
b)
c)
d) x= 4.12
Phương pháp giải:
+) , ( ).
+) Sử dụng quy tắc làm tròn số:
Nếu chữ số đầu tiên bỏ đi nhỏ hơn thì ta giữ nguyên các chữ số còn lại.
Nếu chữ số đầu tiên bỏ đi lớn hơn hoặc bằng thì ta cộng thêm vào chữ số cuối cùng của bộ phận còn lại.
Lời giải:
a) Ta có:
Bấm máy tính ta được:

b) Ta có:
Tính bằng máy tính ta được:
c) Ta có:
Tính bằng máy tính ta được:
d) Ta có:
Tính bằng máy tính ta được:
Bài 4 trang 7 SGK Toán 9 Tập 1: Tìm số x không âm, biết:
a)
b)
c)
d) .
Phương pháp giải:
– Sử dụng công thức với .
– Sử dụng phương pháp bình phương hai vế:
, với , .
Lời giải:
a) Vì nên
Vậy
b) Vì nên
Vậy
c)
Kết hợp với ta có
Vậy
d) Với ta có
Kết hợp điều kiện ta có:
Bài 5 trang 7 SGK Toán 9 Tập 1:Đố. Tính cạnh một hình vuông, biết diện tích của nó bằng diện tích của một hình chữ nhật có chiều rộng 3,5m và chiều dài 14m.
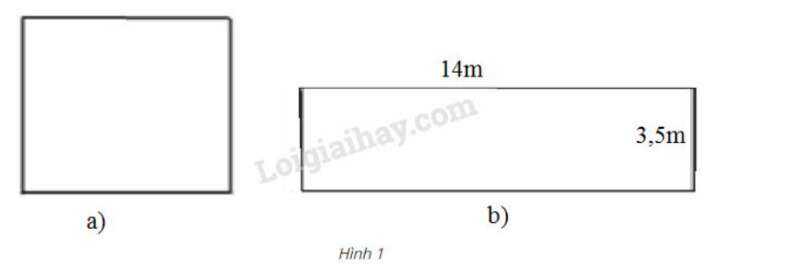
Phương pháp giải:
– Công thức tính diện tích hình vuông cạnh là .
– Công thức tính diện tích hình chữ nhật có chiều dài và chiều rộng lần lượt là là
Lời giải:
Gọi (m) là độ dài hình vuông, .
Diện tích của hình vuông là:
Diện tích của hình chữ nhật là: .
Theo đề bài, diện tích của hình vuông bằng diện tích của hình chữ nhật, nên ta có:
.
Vì nên .
Vậy độ dài cạnh hình vuông là .
Lý thuyết Bài 1: Căn bậc hai
1. Căn thức bậc hai
Căn bậc hai số học
Số dương a có đúng hai căn bậc hai là: và
Với số dương , số được gọi là căn bậc hai số học của .
Số cũng được gọi là căn bậc hai số học của .
+)
+) So sánh hai căn bậc hai số học:
Với hai số không âm ta có .
Căn thức bậc hai
Với là một biểu thức đại số, người ta gọi là căn thức bậc hai của . Khi đó, được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn.
xác định hay có nghĩa khi lấy giá trị không âm.
Chú ý.:
Với ta có:
+ Nếu thì
+ Nếu thì
Ta viết
2. So sánh các căn bậc hai số học
ĐỊNH LÍ:
Với hai số không âm ta có
Ví dụ: So sánh 3 và
Ta có: mà suy ra hay
Hằng đẳng thức
Với mọi số , ta có .
Một cách tổng quát, với là một biểu thức ta có
nghĩa là
nếu và nếu .
3. Một số dạng toán thường gặp
Dạng 1: Tìm căn bậc hai số học và so sánh hai căn bậc hai.
Phương pháp:
Sử dụng kiến thức với hai số không âm ta có .
Dạng 2: Tính giá trị của biểu thức chứa căn bậc hai
Phương pháp:
Sử dụng hằng đẳng thức
Dạng 3: Rút gọn biểu thức chứa căn bậc hai
Phương pháp:
– Đưa các biểu thức dưới dấu căn về hằng đẳng thức (thông thường là , )
– Sử dụng hằng đẳng thức
Dạng 4: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa
Phương pháp:
Sử dụng kiến thức biểu thức có nghĩa khi và chỉ khi
Dạng 5: Giải phương trình chứa căn bậc hai
Phương pháp:
Ta chú ý một số phép biến đổi tương đương liên quan đến căn thức bậc hai sau đây:
;
;