Giải SBT Toán lớp 6 Bài 8: Dấu hiệu chia hết cho 2, cho 5
Bài 66 trang 24 sách bài tập Toán lớp 6 Tập 1: Cho các số 23; 45; 714; 815; 2 300; 2 369; 13 110; 25 555; 4 123 458. Trong các số đó:
a) Số nào chia hết cho 2?
b) Số nào chia hết cho 5?
c) Số nào chia hết cho 2, nhưng không chia hết cho 5?
d) Số nào chia hết cho 5, nhưng không chia hết cho 2?
Lời giải:
a) Các số có tận cùng là các một trong các chữ số: 0; 2; 4; 6; 8 là các số chia hết cho 2.
Trong các số đã cho các số chia hết cho 2 là: 714; 2 300; 13 110; 4 123 458.
b) Các số có chữ số tận cùng là 0 hoặc 5 thì các số đó chia hết cho 5.
Trong các số đã cho các số chia hết cho 5 là: 45; 815; 2 300; 13 110; 25 555.
c) Số chia hết cho 2 nhưng không chia hết cho 5 là: 714; 4 123 458.
d) Số chia hết cho 5 nhưng không chia hết cho 2 là: 45; 815; 25 555.
Bài 67 trang 24 sách bài tập Toán lớp 6 Tập 1: Tìm chữ số x để số 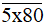 thỏa mãn mỗi điều kiện sau:
thỏa mãn mỗi điều kiện sau:
a) Chia hết cho 2;
b) Chia hết cho 5;
c) Chia hết cho cả 2 và 5.
Lời giải:
a) Số 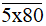 có chữ số tận cùng là 0 nên số này luôn chia hết cho 2.
có chữ số tận cùng là 0 nên số này luôn chia hết cho 2.
Do đó x là chữ số nên có thể nhận tất cả các giá trị {0;1;2;3;4;5;6;7;8;9}.
Vậy x ∈ {0;1;2;3;4;5;6;7;8;9}.
b) Số  có chữ số tận cùng là 0 nên số này luôn chia hết cho 5.
có chữ số tận cùng là 0 nên số này luôn chia hết cho 5.
Do đó x là chữ số nên có thể nhận tất cả các giá trị {0;1;2;3;4;5;6;7;8;9}.
Vậy x ∈ {0;1;2;3;4;5;6;7;8;9}.
c) Số 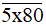 có chữ số tận cùng là 0 nên số này luôn chia hết cho 2 và 5.
có chữ số tận cùng là 0 nên số này luôn chia hết cho 2 và 5.
Do đó x là chữ số nên có thể nhận tất cả các giá trị {0;1;2;3;4;5;6;7;8;9}.
Vậy x ∈ {0;1;2;3;4;5;6;7;8;9}.
Bài 68 trang 24 sách bài tập Toán lớp 6 Tập 1: Tìm chữ số x để số 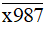 thỏa mãn mỗi điều kiện sau:
thỏa mãn mỗi điều kiện sau:
a) Chia hết cho 2;
b) Chia hết cho 5.
Lời giải:
a) Vì 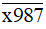 có chữ số tận cùng là 7 nên
có chữ số tận cùng là 7 nên 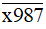 không chia hết cho 2.
không chia hết cho 2.
Do đó không tồn tại giá trị nào của chữ số x để số 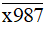 chia hết cho 2.
chia hết cho 2.
Vậy không tồn tại x để  chia hết cho 2.
chia hết cho 2.
b) Vì 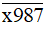 có chữ số tận cùng là 7 nên
có chữ số tận cùng là 7 nên 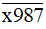 không chia hết cho 5.
không chia hết cho 5.
Do đó không tồn tại giá trị nào của chữ số x để số 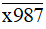 chia hết cho 5.
chia hết cho 5.
Vậy không tồn tại x để 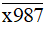 chia hết cho 5.
chia hết cho 5.
Bài 69 trang 24 sách bài tập Toán lớp 6 Tập 1: Tìm chữ số x để số 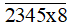 thỏa mãn mỗi điều kiện sau:
thỏa mãn mỗi điều kiện sau:
a) Chia hết cho 4;
b) Chia hết cho 8.
Lời giải:
a) Ta có: 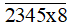 = 234508 + 10.x.
= 234508 + 10.x.
Vì 234 508 = 4.58 627 nên chia hết cho 4.
Để 234 508 + 10.x chia hết cho 4 thì 10.x phải chia hết cho 4 khi đó x ∈ {0;2;4;6;8}.
Vậy x ∈ {0;2;4;6;8}.
b) Ta có: 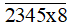 = 234508 + 10.x = 234504 + 4 + 10.x.
= 234508 + 10.x = 234504 + 4 + 10.x.
Vì 234 504 = 8.29 313 nên chia hết cho 8.
Để 234 504 + 4 + 10x chia hết cho 8 thì 4 + 10x chia hết cho 8 khi đó x ∈ {2;6}.
Vậy x ∈ {2;6}.
Bài 70 trang 24 sách bài tập Toán lớp 6 Tập 1: Từ các chữ số 0; 5; 7, hãy viết tất cả các số có ba chữ số khác nhau. Sao cho:
a) Các số đó chia hết cho 2;
b) Các số đó chia hết cho 5;
c) Các số đó chia hết cho 5, nhưng không chia hết cho 2;
d) Các số đó chia hết cho cả 2 và 5.
Lời giải:
a) Các số chia hết cho 2 có tận cùng là 0; 2; 4; 6; 8 nên số chia hết cho 2 tạo bởi 3 chữ số 0; 5; 7 là: 570; 750.
b) Các số chia hết cho 5 có tận cùng là 0 hoặc 5 nên số chia hết cho 5 tạo bởi 3 chữ số 0; 5; 7 là: 570; 750; 705.
c) Các số chia hết cho 5 nhưng không chia hết cho 2 là: 705.
d) Các số chia hết cho cả 2 và 5 là: 570; 750.
Bài 71 trang 25 sách bài tập Toán lớp 6 Tập 1: Không tính giá trị biểu thức, hãy giải thích tại sao mỗi biểu thức sau chia hết cho 2:
a) A = 1 234 + 43 312 + 5 436 + 10 988;
b) B = 2 335 + 983 333 + 3 142 311 + 5 437;
c) C = 11 + 22 + 33 + … + 88 + 99 + 2 021;
d) D = 8.51.633.4 445 – 777.888 + 2 020.
Lời giải:
a) Vì 1 234 có chữ số tận cùng là 4 nên chia hết cho 2;
43 312 có chữ số tận cùng là 2 nên chia hết cho 2;
5 436 có chữ số tận cùng là 6 nên chia hết cho 2;
10 988 có chữ số tận cùng là 8 nên chia hết cho 2.
Do đó 1 234 + 43 312 + 5 436 + 10 988 chia hết cho 2.
Vậy A = 1 234 + 43 312 + 5 436 + 10 988 chia hết cho 2.
b) Vì 2 335; 983 333; 3 142 311; 5 437 là các số lẻ nên tổng của 2 335 + 983 333 + 3 142 311 + 5 437 là số chẵn nên chia hết cho 2.
Vậy B = 2 335 + 983 333 + 3 142 311 + 5 437 chia hết cho 2.
c) 11 + 22 + 33 + … + 88 + 99 + 2 021
Vì 11; 33; 55; 77; 99; 2 021 là các số lẻ nên 11 + 33 + 55 + 77 + 99 + 2 021 là một chẵn nên chia hết cho 2.
Mà các số 22; 44; 66; 88 đều là các số chẵn nên chia hết cho 2.
d) Vì 8 chia hết cho 2 nên 8.51.633.4 445 chia hết cho 2; 888 chia hết cho 2 nên 777.888 chia hết cho 2 và 2 020 chia hết cho 2 nên 8.51.633.4 445 – 777.888 + 2 020 chia hết cho 2.
Vậy D = 8.51.633.4 445 – 777.888 + 2 020 chia hết cho 2.
Bài 72 trang 25 sách bài tập Toán lớp 6 Tập 1: Tìm số tự nhiên có ba chữ số giống nhau, biết rằng số đó không chia hết cho 2 nhưng chia hết cho 5.
Lời giải:
Các số chia hết cho 5 có chữ số tận cùng là 0 hoặc 5.
Mà số cần tìm không chia hết cho 2 nên chữ số tận cùng là 5.
Số cần tìm là số có ba chữ số giống nhau nên số đó là: 555.
Vậy số tự nhiên có ba chữ số cần tìm là: 555.
Bài 73 trang 25 sách bài tập Toán lớp 6 Tập 1:
a) Có bao nhiêu số có hai chữ số chia cho 5 dư 4?
b) Có bao nhiêu số có ba chữ số chia cho 2 và cho 5 có cùng số dư?
c) Từ 1 đến 555 có bao nhiêu số chia hết cho 2?
d) Từ 500 đến 1 000 có bao nhiêu số chia hết cho 5?
Lời giải:
a) Các số có hai chữ số chia 5 dư 4 là: 14; 19; 24; 29; 34; 39; 44; …; 94; 99.
Số các số có hai chữ số chia 5 dư 4 là: (99 – 14):5 + 1 = 18.
Vậy có 18 số có hai chữ số chia cho 5 dư 4.
b) Một số chia cho 2 sẽ có số dư là 0; 1.
Một số chia cho 5 sẽ có số dư là: 0; 1; 2; 3; 4.
Do đó, một số chia cho 2 và cho 5 có cùng số dư thì số đó phải chia hết cho cả 2 và 5 hoặc cùng chia cho 2 và cho 5 dư 1.
Trường hợp 1: Các số có ba chữ số cùng chia hết cho 2 và cho 5 là: 100; 110; 120; …; 990.
Số các số có ba chữ số cùng chia hết cho 2 và 5 là: (990 – 100):10 + 1 = 90 số.
Trường hợp 2: Các số có ba chữ số cùng chia cho 2 và cho 5 có số dư là 1 là: 101; 111; 121; …; 991.
Số các số có ba chữ số cùng chia cho 2 và cho 5 dư 1 là: (991 – 101):10 + 1 = 90 số.
Vậy có tất cả 90 + 90 = 180 số có ba chữ số chia cho 2 và cho 5 có cùng số dư.
c) Các số chia hết cho 2 từ 1 đến 555 là: 2; 4; 6; …; 554.
Số các số nằm trong khoảng từ 1 đến 555 chia hết cho 2 là: (554 – 2):2 + 1 = 277 số.
Vậy có 277 số trong các số từ 1 đến 555 chia hết cho 2.
d) Các số từ 500 đến 1 000 chia hết cho 5 là: 500; 505; 510; …; 1000.
Số các số nằm từ 500 đến 1 000 chia hết cho 5 là: (1 000 – 500):5 + 1 = 101 số.
Vậy có tất cả 101 số từ 500 đến 1 000 chia hết cho 5.
Bài 74 trang 25 sách bài tập Toán lớp 6 Tập 1: Một cửa hàng mĩ phẩm miễn thuế ở sân bay có khuyên mãi như sau: Khách cứ mua 10 hộp mĩ phẩm thì được tặng một hộp. Mỗi hộp có giá 53 USD. Công ty A mua 48 hộp mĩ phẩm ở cửa hàng đó. Hỏi số USD công ty phải trả để mua 48 mĩ phẩm trên có chia hết cho 5 không? Vì sao?
Lời giải:
Ta có 48 = 4.10 + 8.
Vì mua 10 hộp được tặng 1 hộp nên trong 40 hộp công ty A mua sẽ được tặng 4 hộp mĩ phẩm nữa nên công ty phải trả tiền cho 44 hộp mĩ phẩm.
Công ty phải trả số tiền để mua 48 hộp mĩ phẩm trên là: 44.53 = 2 332 (USD).
Mà 2 332 có chữ số tận cùng là 2 nên không chia hết cho 5.
Bài 75 trang 25 sách bài tập Toán lớp 6 Tập 1: Chứng tỏ rằng:
a) Tổng của 2 020 số lẻ bất kì luôn chia hết cho 2;
b) 1111 + 2222 + 3333 + 4444 + 5555 không chia hết cho 2;
c) 2 + 22 + 23 + … + 259 + 260 + 561 chia hết cho 5.
Lời giải:
a) Tổng của hai số lẻ bất kì là một số chẵn nên tổng của 2020 số lẻ bất kì là một số chẵn nên chia hết cho 2.
b) Ta có 11 là số lẻ nên 1111 là số lẻ;
33 là số lẻ nên 3333 là số lẻ;
55 là số lẻ nên 5555 là số lẻ;
Khi đó: 1111 + 3333 + 5555 là số lẻ.
Mặt khác 2222; 4444 là các số chẵn nên 2222 + 4444 là số chẵn.
Vậy 1111 + 2222 + 3333 + 4444 + 5555 là số lẻ nên không chia hết cho 2.
c) Xét 2 + 22 + 23 + … + 259 + 260
= (2 + 22 + 23 + 24) + (25 + 26 + 27 + 28) + … + (257 + 258 + 259 + 260)
= 2(1 + 2 + 22 + 23) + 25.(1 + 2 + 22 + 23) + … + 257.(1 + 2 + 22 + 23)
= 2.15 + 25.15 + … + 257.15
= 15.(2 + 25 + … + 257)
Vì 155 nên 15.(2 + 25 + … + 257)5 mà 561 cũng chia hết cho 5.
Nên 2 + 22 + 23 + … + 259 + 260 + 561 chia hết cho 5.
Vậy 2 + 22 + 23 + … + 259 + 260 + 561 chia hết cho 5.
Bài 76 trang 25 sách bài tập Toán lớp 6 Tập 1:
Bạn Duyên sử dụng các khối lập phương để xếp hình. Các hình bạn Duyên xếp được qua các lần được biểu diễn như dưới đây:
Hỏi số khối lập phương bạn Duyên dùng cho lần xếp hình thứ 100 có chia hết cho cả 2 và 5 hay không?
Lời giải:
Qua các lần xếp hình ta thấy số khối lập phương được xếp ở hàng 1 bằng đúng lần đó và các hàng trên giảm dần về 1.
Do đó hàng 1 của lần xếp hình thứ 100 là 100 khối lập phương, hàng tiếp theo là 99 khối, hàng tiếp theo là 98, … đến hàng cuối cùng sẽ có 1 khối lập phương.
Số khối lập phương bạn Duyên dùng cho lần xếp hình thứ 100 là:
100 + 99 + 98 + … + 2 + 1
= (100 + 1) + (99 + 2) + (98 + 3) + … + (50 + 51)
= 101 + 101 + 101 + … + 101
= 101.60
= 5 050.
Ta thấy 5 050 có tận cùng là chữ số 0 nên 5 050 chia hết cho 2 và 5.
Vậy có 5 050 khối lập phương được dùng cho lần xếp hình thứ 100 của bạn Duyên va chia hết cho 2 và 5.
====== ****&**** =====