Giải SGK Toán 9 Bài 3: Giải hệ phương trình bằng phương pháp thế

By 0

Giải bài tập Toán lớp 9 Bài 3: Giải hệ phương trình bằng phương pháp thế

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 14 Toán 9 Tập 2: Giải hệ phương trình sau bằng phương pháp thế (biểu diễn y theo x từ phương trình thứ hai của hệ)

Lời giải:

4x−5y=33x−y=16⇔4x−5y=3   (1)y=3x−16   (2)

Thay (2) vào (1) ta được:

4x−53x−16=3y=3x−16⇔4x−15x+80=3y=3x−16⇔−11x=3−80y=3x−16⇔−11x=−77y=3x−16⇔x=(−77):(−11)y=3x−16⇔x=7y=3.7−16⇔x=7y=5

Vậy hệ phương trình có nghiệm duy nhất (x; y) = (7; 5)

Câu hỏi 2 trang 15 Toán 9 Tập 2: Bằng minh họa hình học, hãy giải thích tại sao hệ (III) có vô số nghiệm.

Lời giải:

4x−2y=−6−2x+y=3(III)

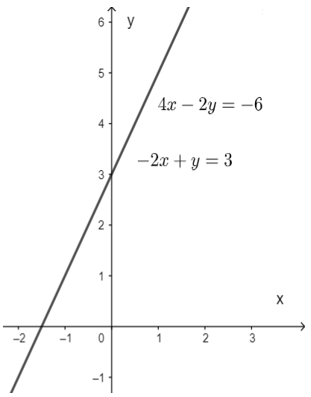
Vẽ đường thẳng 4x – 2y = -6

Cho x = 0 ⇒y = 3⇒(0; 3)

Cho y = 0 ⇒x=−32⇒−32;0

Đường thẳng 4x – 3y = -6 đi qua hai điểm (0; 3) và −32;0

Vẽ đường thẳng -2x + y = 3

Cho x = 0 ⇒y = 3⇒(0; 3)

Cho y = 0⇒x=−32⇒−32;0

Đường thẳng -2x + y = 3 đi qua hai điểm (0; 3) và −32;0

Từ đồ thị ta thấy đường thẳng trùng nhau nên hệ đã cho có vô số nghiệm.

Tài liệu VietJack

Câu hỏi 3 trang 15 Toán 9 Tập 2: Cho hệ phương trình:

(IV)4x+y=28x+2y=1

Bằng minh họa hình học và bằng phương pháp thế, chứng tỏ rằng hệ (IV) vô nghiệm.

Lời giải:

*) Bằng minh họa hình học

– Xét đường thẳng (d): 4x + y = 2 hay y = -4x + 2

Cho x = 0 ⇒y=2⇒0;2

Cho y = 0⇒x=12⇒12;0

Đường thẳng (d) đi qua hai điểm (0; 2) và 12;0

– Xét đường thẳng (d’): 8x + 2y = 1 hay y = -4x +12

Cho x = 0 ⇒y=12⇒0;12

Cho y = 0 ⇒x=18⇒18;0

Đường thẳng (d’) đi qua hai điểm 0;12 và 18;0

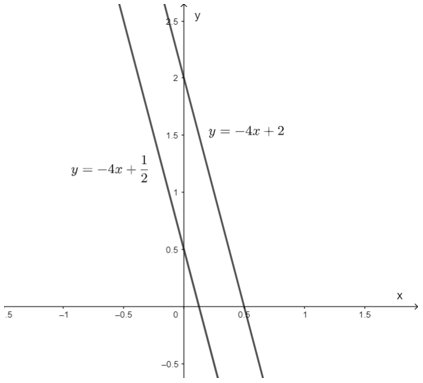
Tài liệu VietJack

Từ hình vẽ trên ta thấy hai đường thẳng đã cho song song nên hệ phương trình vô nghiệm.

*) Bằng phương pháp thế:

(IV)4x+y=28x+2y=1⇔y=2−4x8x+22−4x=1

⇔8x+4−8x=1y=2−4x⇔4=1y=2−4x(Vô lí)

Vậy hệ đã cho vô nghiệm

Bài tập (trang 15)

Bài 12 trang 15 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp thế:

a) x−y=33x−4y=2

b) 7x−3y=54x+y=2

c) x+3y=−25x−4y=11

Lời giải:

a)

x−y=33x−4y=2⇔x=3+y3x−4y=2⇔x=3+y33+y−4y=2⇔x=3+y9+3y−4y=2⇔x=3+y9+3y−4y=2⇔x=y+3y=9−2⇔x=y+3y=7⇔x=7+3y=7⇔x=10y=7

Vậy hệ phương trình đã cho có nghiệm (x; y) = (10; 7)

b)

7x−3y=54x+y=2⇔7x−3y=5y=2−4x⇔7x−3.2−4x=5y=2−4x⇔7x−6+12x=5y=2−4x⇔19x=5+6y=2−4x⇔19x=11y=2−4x⇔x=1119y=2−4.1119⇔x=1119y=−619

Vậy hệ phương trình đã cho có nghiệm (x; y) = 1119;−619.

c)

x+3y=−25x−4y=11⇔x=−2−3y5−2−3y−4y=11⇔x=−2−3y−10−15y−4y=11⇔x=−2−3y−19y=10+11⇔x=−2−3y−19y=21⇔x=−2−3yy=−2119⇔x=−2−3.−2119y=−2119⇔x=2519y=−2119

Vậy hệ phương trình đã cho có nghiệm (x; y) = 2519;−2119.

Bài 13 trang 15 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp thế:

a) 3x−2y=114x−5y=3

b) x2−y3=15x−8y=3

Lời giải:

a)

3x−2y=114x−5y=3⇔3x=11+2y4x−5y=3⇔x=11+2y34x−5y=3⇔x=11+2y34.11+2y3−5y=3⇔x=11+2y344+8y3−5y=3⇔x=11+2y344+8y−15y=9⇔x=11+2y37y=35⇔x=11+2.53y=5⇔x=7y=5

Vậy hệ phương trình đã cho có nghiệm (x; y) là (7; 5)

b)

x2−y3=15x−8y=3⇔x2=1+y35x−8y=3⇔x=1+y3.25x−8y=3⇔x=2+23y52+23y−8.y=3⇔x=2+23y10+103y−8y=3⇔x=2+23y−143y=3−10⇔x=2+23y−143y=−7⇔x=2+23yy=−7:−143⇔x=2+23yy=32⇔x=2+23.32y=32⇔x=3y=32

Vậy hệ phương trình đã cho có nghiệm (x; y) = 3;32.

Bài 14 trang 15 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp thế:

a) x+y5=0x5+3y=1−5

b) 2−3x−3y=2+534x+y=4−23

Lời giải:

a) 

x+y5=0x5+3y=1−5⇔x=−y5−y5.5+3y=1−5⇔x=−y5y−5+3=1−5⇔x=−y5−2y=1−5⇔x=−5yy=1−5−2⇔x=−5yy=5−12⇔x=−5.5−12y=5−12⇔x=5−52y=5−12

Vậy hệ phương trình đã cho có nghiệm (x; y) =5−52;5−12

b)

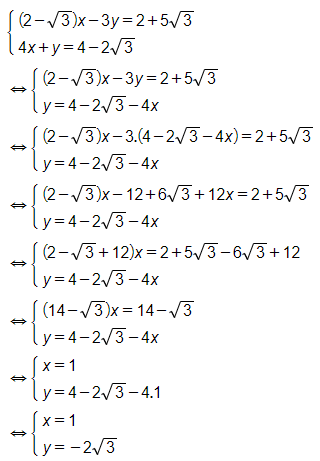
Giải các hệ phương trình sau bằng phương pháp thế: x + y căn 5 = 0 (ảnh 1)

Vậy phương trình đã cho có nghiệm (x; y) là (1; −23).

Luyện tập trang 15, 16

Bài 15 trang 15 SGK Toán 9 Tập 2: Giải hệ phương trình x+3y=1a2+1x+6y=2a trong mỗi trường hợp sau:

a) a = -1;

b) a = 0;

c) a = 1.

Lời giải:

x+3y=1a2+1x+6y=2a⇔x=1−3ya2+11−3y+6y=2a

a) Thay a = -1 vào hệ phương trình ta được

x=1−3y−12+11−3y+6y=2.−1⇔x=1−3y2.1−3y+6y=−2⇔x=1−3y2−6y+6y=−2

⇔x=1−3y2=−2 (vô lí)

Vậy với a = – 1 hệ phương trình đã cho vô nghiệm.

b) Thay a = 0 vào hệ phương trình ta được

x=1−3y02+11−3y+6y=2.0⇔x=1−3y1−3y+6y=0⇔x=1−3y3y=−1⇔x=1−3yy=−13⇔x=1−3.−13y=−13⇔x=2y=−13

Vậy với a = 0 hệ phương trình đã cho có nghiệm duy nhất (x; y) =2;−13

c) Thay a = 1 vào hệ phương trình ta có:

x=1−3y12+11−3y+6y=2.1⇔x=1−3y2.1−3y+6y=2⇔x=1−3y2−6y+6y=2

⇔x=1−3y2=2 (luôn đúng)

Vậy với a = 1 hệ phương trình đã cho có vô số nghiệm dạng (1 – 3y; y) với y∈ℝ

Bài 16 trang 16 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp thế:

a) 3x−y=55x+2y=23

b) 3x+5y=12x−y=−8

c) xy=23x+y−10=0

Lời giải:

a)

3x−y=55x+2y=23⇔y=3x−55x+2.3x−5=23⇔5x+6x−10=23y=3x−5⇔11x=23+10y=3x−5⇔11x=33y=3x−5⇔x=33:11y=3x−5⇔x=3y=3.3−5⇔x=3y=4

Vậy hệ phương trình đã cho có nghiệm là (x; y) = (3; 4)

b)

3x+5y=12x−y=−8⇔3x+5y=1y=2x+8⇔3x+52x+8=1y=2x+8⇔3x+10x+40=1y=2x+8⇔13x=1−40y=2x+8⇔13x=−39y=2x+8⇔x=−39:13y=2x+8⇔x=−3y=2.−3+8⇔x=−3y=2

Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) = (-3; 2).

c)

xy=23x+y−10=0⇔x=23y23y+y−10=0⇔x=23y53y=10⇔x=23yy=10:53⇔x=23yy=6⇔x=23.6y=6⇔x=4y=6

Vậy hệ phương trình đã cho có nghiệm (x; y) = (4; 6).

Bài 17 trang 16 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp thế:

a) x2−y3=1x+y3=2

b) x−22y=5x2+y=1−10

c) 2−1x−y=2x+2+1y=1

Lời giải:

a)

x2−y3=1x+y3=2⇔x2−y3=1x=2−y3⇔2−y32−y3=1x=2−y3⇔2−y6−y3=1x=2−y3⇔y−6−3=1−2x=2−y3⇔y6+3=1x=2−y3⇔y=16+3x=2−y3⇔y=6−33x=2−6−33.3⇔x=1y=6−33

Vậy hệ phương trình đã cho có nghiệm (x; y) = 1;6−33

b)

x−22y=5x2+y=1−10⇔x=5+22y5+22y2+y=1−10⇔x=5+22y10+4y+y=1−10⇔x=5+22y5y=1−10−10⇔x=5+22y5y=1−210⇔x=5+22yy=1−2105⇔x=5+22.1−2105y=1−2105⇔x=5+22−22.2105y=1−2105⇔x=−35+225y=1−2103

Vậy hệ phương trình đã cho có nghiệm (x; y) = −35+225;1−2103

c)

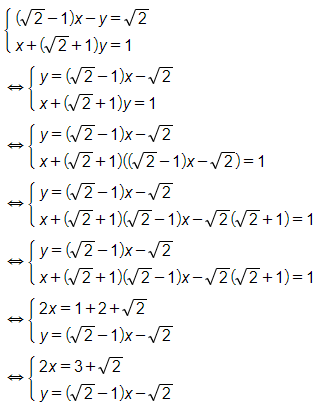
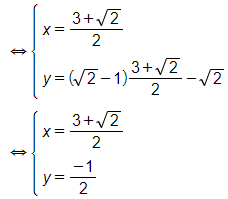
Giải các hệ phương trình sau bằng phương pháp thế: x căn 2 - y căn 3 = 1 (ảnh 1)

Giải các hệ phương trình sau bằng phương pháp thế: x căn 2 - y căn 3 = 1 (ảnh 1)

Vậy hệ phương trình đã cho có nghiệm (x; y) =3+22;−12

Bài 18 trang 16 SGK Toán 9 Tập 2: a) Xác định các hệ số a và b, biết rằng hệ phương trình 2x+by=−4bx−ay=−5 có nghiệm (1; -2).

b) Cũng hỏi như vậy nếu phương trình có nghiệm là 2−1;2

Lời giải:

a) Vì hệ phương trình có nghiệm (1; -2) nên x = 1 và y = -2 thỏa mãn cả hai phương trong trong hệ.

Thay x = 1 và y = -2 vào hệ ta được:

2.1+b.(−2)=−4b.1−a.(−2)=−5⇔2−2b=−4b+2a=−5⇔−2b=−4−2b+2a=−5⇔−2b=−6b+2a=−5⇔b=33+2a=−5⇔2a=−5−3b=3⇔2a=−8b=3⇔a=−4b=3

Vậy để hệ phương trình đã cho có nghiệm là (1; -2) thì a = -4 và b = 3.

b) Vì hệ phương trình có nghiệm 2−1;2 nên x =2−1  và y = 2 thỏa mãn cả hai phương trong trong hệ.

Thay x = 2−1 và y =2 vào hệ ta được:

2.2−1+b.2=−4b.2−1−a.2=−5

⇔22−2+b2=−4b2−1−a2=−5

⇔b2=−4+2−22b2−1−a2=−5⇔2b=−2−22b2−1−a2=−5

⇔b=−2−222b2−1−a2=−5⇔b=−2−2b2−1−a2=−5⇔b=−2−2−2−22−1−a2=−5

⇔b=−2−2−22−2+2+2−a2=−5⇔b=−2−2−a2=−5+22+2−2−2

⇔b=−2−2−a2=−5+2⇔a=−5+2−2b=−2−2⇔a=52−22b=−2−2

Vậy để hệ phương trình đã cho có nghiệm là 2−1;2 thì a =52−22 và b = -2 –2

Bài 19 trang 16 SGK Toán 9 Tập 2: Biết rằng: Đa thức P(x) chia hết cho đa thức x – a khi và chỉ khi P(a) = 0. Hãy tìm các giá trị của m và n sao cho đa thức sau đồng thời chia hết cho x + 1 và x – 3:

P(x) = mx3 + (m – 2)x2 – (3n – 5)x – 4n

Lời giải

+ P(x) chia hết cho x + 1

⇔ P(-1) = 0

⇔ m.(-1)3 + (m – 2)(-1)2 – (3n – 5).(-1) – 4n = 0

⇔ -m + m – 2 + 3n – 5 – 4n = 0

⇔ -n – 7 = 0

⇔ n = -7 (1)

Vậy với mọi m và n = -7 thì P(x) chia hết cho x + 1

+ P(x) chia hết cho x – 3

⇔ P(3) = 0

⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0

⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0

⇔ 36m – 13n = 3 (2)

Từ (1) và (2) ta có hệ phương trình:

n=−736m−13n=3⇔n=−736m−13.−7=3⇔n=−736m+91=3⇔n=−736m=3−91

⇔n=−736m=−88⇔n=−7m=−229

Vậy n = -7; m =−229  thì P(x) chia hết cho x – 3.

Bài liên quan:

Leave a Comment

Back to Top
Menu