SBT Toán 9 Bài 3: Giải hệ phương trình bằng phương pháp thế | Giải SBT Toán lớp 9

Giải SBT Toán 9 Bài 3: Giải hệ phương trình bằng phương pháp thế

Bài 16 trang 9 SBT Toán 9 tập 2: Giải các hệ phương trình sau bằng phương pháp thế: 

a) $\{\begin{array}{c}4x+5y=3\\ x-3y=5\end{array}$

b) $\{\begin{array}{c}7x-2y=1\\ 3x+y=6\end{array}$

c) $\{\begin{array}{c}1,3x+4,2y=12\\ 0,5x+2,5y=5,5\end{array}$

d)$\{\begin{array}{c}\sqrt{5}x-y=\sqrt{5}\left(\sqrt{3}-1\right)\\ 2\sqrt{3}x+3\sqrt{5}y=21\end{array}$

Phương pháp giải:

Sử dụng:

– Cách giải hệ phương trình bằng phương pháp thế:

+ Bước $1$: Rút $x$ hoặc $y$ từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn.

+ Bước $2$: Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.

Lời giải:

a)

$\begin{array}{rl}& \{\begin{array}{c}4x+5y=3\\ x-3y=5\end{array}\\ & \iff \{\begin{array}{c}x=3y+5\\ 4\left(3y+5\right)+5y=3\end{array}\\ & \iff \{\begin{array}{c}x=3y+5\\ 17y=-17\end{array}\\ & \iff \{\begin{array}{c}x=3y+5\\ y=-1\end{array}\\ & \iff \{\begin{array}{c}x=2\\ y=-1\end{array}\end{array}$

Vậy hệ phương trình có nghiệm duy nhất là $(x;y)=(2;-1).$

b)

$\begin{array}{rl}& \{\begin{array}{c}7x-2y=1\\ 3x+y=6\end{array}\\ & \iff \{\begin{array}{c}y=-3x+6\\ 7x-2\left(-3x+6\right)=1\end{array}\\ & \iff \{\begin{array}{c}y=-3x+6\\ 13x=13\end{array}\\ & \iff \{\begin{array}{c}x=1\\ y=-3x+6\end{array}\\ & \iff \{\begin{array}{c}x=1\\ y=3\end{array}\end{array}$

Vậy hệ phương trình có nghiệm duy nhất là $(x;y)=(1;3)$.

 c)

$\begin{array}{rl}& \{\begin{array}{c}1,3x+4,2y=12\\ 0,5x+2,5y=5,5\end{array}\\ & \iff \{\begin{array}{c}1,3x+4,2y=12\\ x+5y=11\end{array}\\ & \iff \{\begin{array}{c}x=11-5y\\ 1,3\left(11-5y\right)+4,2y=12\end{array}\\ & \iff \{\begin{array}{c}x=11-5y\\ -23y=-23\end{array}\\ & \iff \{\begin{array}{c}x=11-5y\\ y=1\end{array}\\ & \iff \{\begin{array}{c}x=6\\ y=1\end{array}\end{array}$

Vậy hệ phương trình có nghiệm duy nhất là $(x;y)=(6;1)$.

 d)

$\begin{array}{rl}& \{\begin{array}{c}\sqrt{5}x-y=\sqrt{5}\left(\sqrt{3}-1\right)\\ 2\sqrt{3}x+3\sqrt{5}y=21\end{array}\\ & \iff \{\begin{array}{c}y=\sqrt{5}\left(x+1-\sqrt{3}\right)\\ 2\sqrt{3}x+15\left(x+1-\sqrt{3}\right)=21\end{array}\\ & \iff \{\begin{array}{c}y=\sqrt{5}\left(x+1-\sqrt{3}\right)\\ \left(2\sqrt{3}+15\right)x=6+15\sqrt{3}\end{array}\\ & \iff \{\begin{array}{c}y=\sqrt{5}\left(x+1-\sqrt{3}\right)\\ x=\frac{6+15\sqrt{3}}{2\sqrt{3}+15}\end{array}\end{array}$

$\begin{array}{l}\iff \{\begin{array}{l}y=\sqrt{5}\left(x+1-\sqrt{3}\right)\\ x=\frac{\sqrt{3}\left(2\sqrt{3}+15\right)}{2\sqrt{3}+15}\end{array}\\ \iff \{\begin{array}{l}y=\sqrt{5}\left(x+1-\sqrt{3}\right)\\ x=\sqrt{3}\end{array}\\ \iff \{\begin{array}{l}x=\sqrt{3}\\ y=\sqrt{5}\left(\sqrt{3}+1-\sqrt{3}\right)\end{array}\\ \iff \{\begin{array}{l}x=\sqrt{3}\\ y=\sqrt{5}\end{array}\end{array}$

Vậy hệ phương trình có nghiệm duy nhất là $(x;y)=\left(\sqrt{3};\sqrt{5}\right).$

Bài 17 trang 9 SBT Toán 9 tập 2: Giải các hệ phương trình:

a) $\{\begin{array}{c}1,7x-2y=3,8\\ 2,1x+5y=0,4\end{array}$

b) $\{\begin{array}{c}\left(\sqrt{5}+2\right)x+y=3-\sqrt{5}\\ -x+2y=6-2\sqrt{5}\end{array}$

Phương pháp giải:

Sử dụng:

– Cách giải hệ phương trình bằng phương pháp thế:

+ Bước $1$: Rút $x$ hoặc $y$ từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn.

+ Bước $2$: Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.

Lời giải:

a)

$\begin{array}{rl}& \{\begin{array}{c}1,7x-2y=3,8\\ 2,1x+5y=0,4\end{array}\\ & \iff \{\begin{array}{c}17x-20y=38\\ 21x+50y=4\end{array}\\ & \iff \{\begin{array}{c}y=\frac{17x-38}{20}\\ 21x+50.\frac{17x-38}{20}=4\end{array}\\ & \iff \{\begin{array}{c}y=\frac{17x-38}{20}\\ 42x+85x-190=8\end{array}\\ & \iff \{\begin{array}{c}y=\frac{17x-38}{20}\\ 127x=198\end{array}\\ & \iff \{\begin{array}{c}y=\frac{17x-38}{20}\\ x=\frac{198}{127}\end{array}\\ & \iff \{\begin{array}{c}y=-\frac{73}{127}\\ x=\frac{198}{127}\end{array}\end{array}$

Vậy hệ phương trình đã cho có nghiệm duy nhất: $(x;y)=\left(\frac{198}{127};-\frac{73}{127}\right).$

b)

Vậy hệ phương trình đã cho có nghiệm duy nhất là: $(x;y)=\left(0;3-\sqrt{5}\right)$.

Bài 18 trang 9 SBT Toán 9 tập 2: Tìm giá trị của $a$ và $b$:

a) Để hệ phương trình

$\{\begin{array}{c}3ax-\left(b+1\right)y=93\\ bx+4ay=-3\end{array}$

có nghiệm là $(x;y)=(1;-5)$;

b) Để hệ phương trình

$\{\begin{array}{c}\left(a-2\right)x+5by=25\\ 2ax-\left(b-2\right)y=5\end{array}$

có nghiệm là $(x;y)=(3;-1)$

Phương pháp giải:

Sử dụng:

– Cặp số $(x_0;y_0)$ là nghiệm của hệ phương trình 

$\{\begin{array}{c}ax+by=c\\ a^{\prime }x+b^{\prime }y=c^{\prime }\end{array}\iff \{\begin{array}{c}a{x}_0+b{y}_0=c\\ a^{\prime }{x}_0+b^{\prime }{y}_0=c^{\prime }\end{array}$

– Cách giải hệ phương trình bằng phương pháp thế (coi $a,b$ là ẩn)

+ Bước $1$: Rút $a$ hoặc $b$ từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn.

+ Bước $2$: Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.

Lời giải:

a)

Để cặp $(x;y)=(1;-5)$ là nghiệm của hệ phương trình đã cho, ta thay $x=1;y=-5$ vào hệ phương trình ta được:

$\begin{array}{l}\{\begin{array}{l}3a.1-\left(b+1\right).\left(-5\right)=93\\ b.1+4a.\left(-5\right)=-3\end{array}\\ \iff \{\begin{array}{l}3a+5b+5=93\\ b-20a=-3\end{array}\end{array}$

$\begin{array}{rl}& \iff \{\begin{array}{c}3a+5b=88\\ b-20a=-3\end{array}\\ & \iff \{\begin{array}{c}b=20a-3\\ 3a+5\left(20a-3\right)=88\end{array}\\ & \iff \{\begin{array}{c}b=20a-3\\ 3a+100a-15=88\end{array}\\ & \iff \{\begin{array}{c}b=20a-3\\ 103a=103\end{array}\\ & \iff \{\begin{array}{c}b=20a-3\\ a=1\end{array}\\ & \iff \{\begin{array}{c}b=17\\ a=1\end{array}\end{array}$

Vậy $a=1$ và $b=17.$

 b)

Để cặp $(x;y)=(3;-1)$ là nghiệm của hệ phương trình đã cho, ta thay $x=3;y=-1$ vào hệ phương trình ta được:

$\begin{array}{l}\{\begin{array}{l}\left(a-2\right).3+5b.\left(-1\right)=25\\ 2a.3-\left(b-2\right).\left(-1\right)=5\end{array}\\ \iff \{\begin{array}{l}3a-6-5b=25\\ 6a+b-2=5\end{array}\end{array}$

$\begin{array}{rl}& \iff \{\begin{array}{c}3a-5b=31\\ 6a+b=7\end{array}\\ & \iff \{\begin{array}{c}b=7-6a\\ 3a-5\left(7-6a\right)=31\end{array}\\ & \iff \{\begin{array}{c}b=7-6a\\ 33a=66\end{array}\\ & \iff \{\begin{array}{c}b=7-6a\\ a=2\end{array}\\ & \iff \{\begin{array}{c}b=-5\\ a=2\end{array}\end{array}$

Vậy  $a=2$ và  $b=-5.$

Bài 19 trang 9 SBT Toán 9 tập 2: Tìm giá trị của $a$ và $b$ để hai đường thẳng

$(d_1)$:  $\left(3a-1\right)x+2by=56$ 

và $(d_2)$:  $\frac{1}{2}ax-\left(3b+2\right)y=3$ 

cắt nhau tại điểm $M(2;-5).$

Phương pháp giải:

Sử dụng:

– Hai đường thẳng $(d_1)$:  $ax+by=c$ và $(d_2)$:  $a^{\prime }x+b^{\prime }y=c^{\prime }$ cắt nhau tại điểm $M$  thì tọa độ của $M$ là nghiệm của hệ phương trình: $\{\begin{array}{c}ax+by=c\\ a^{\prime }x+b^{\prime }y=c^{\prime }\end{array}$

– Cặp số $(x_0;y_0)$ là nghiệm của hệ phương trình 

$\{\begin{array}{c}ax+by=c\\ a^{\prime }x+b^{\prime }y=c^{\prime }\end{array}$

$\iff \{\begin{array}{c}a{x}_0+b{y}_0=c\\ a^{\prime }{x}_0+b^{\prime }{y}_0=c^{\prime }\end{array}$

– Cách giải hệ phương trình bằng phương pháp thế (coi $a,b$ là ẩn)

+ Bước $1$: Rút $a$ hoặc $b$ từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn.

+ Bước $2$: Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.

Lời giải:

Hai đường thẳng $(d_1)$: $\left(3a-1\right)x+2by=56$ và  

$(d_2)$: $\frac{1}{2}ax-\left(3b+2\right)y=3$ cắt nhau tại điểm $M(2;-5)$ nên tọa độ của $M$ là nghiệm của hệ phương trình:

$\{\begin{array}{c}\left(3a-1\right)x+2by=56\\ \frac{1}{2}ax-\left(3b+2\right)y=3\end{array}$

Thay $x=2$ và $y=-5$ vào hệ phương trình ta có:

$\begin{array}{rl}& \{\begin{array}{c}2\left(3a-1\right)+2b\left(-5\right)=56\\ \frac{1}{2}a.2-\left(3b+2\right).\left(-5\right)=3\end{array}\\ & \iff \{\begin{array}{c}6a-10b=58\\ a+15b+10=3\end{array}\\ & \iff \{\begin{array}{c}3a-5b=29\\ a+15b=-7\end{array}\\ & \iff \{\begin{array}{c}a=-7-15b\\ 3\left(-7-15b\right)-5b=29\end{array}\\ & \iff \{\begin{array}{c}a=-7-15b\\ -50b=50\end{array}\\ & \iff \{\begin{array}{c}a=-7-15b\\ b=-1\end{array}\\ & \iff \{\begin{array}{c}a=8\\ b=-1\end{array}\end{array}$

Vậy $a=8;b=-1.$ 

 

Bài 20 trang 9 SBT Toán 9 tập 2: Tìm $a$ và $b:$

a) Để đường thẳng $y=ax+b$ đi qua hai điểm $A(-5;3)$, $B\left(\frac{3}{2};-1\right)$;

b) Để đường thẳng $ax-8y=b$ đi qua điểm $M(9;-6)$ và đi qua giao điểm của hai đường thẳng $(d_1)$:  $2x+5y=17,$

 $(d_2)$: $4x-10y=14$

Phương pháp giải:

Sử dụng:

– Đường thẳng $ax+by=c$ đi qua điểm $M(x_0;y_0)$ $\iff a{x}_0+b{y}_0=c$.

– Cách giải hệ phương trình bằng phương pháp thế:

+ Bước $1$: Rút $x$ hoặc $y$ từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn.

+ Bước $2$: Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.

– Hai đường thẳng $(d_1)$:  $ax+by=c$ và $(d_2)$:  $a^{\prime }x+b^{\prime }y=c^{\prime }$ cắt nhau tại điểm $M$  thì tọa độ của $M$ là nghiệm của hệ phương trình: $\{\begin{array}{c}ax+by=c\\ a^{\prime }x+b^{\prime }y=c^{\prime }\end{array}$

Lời giải:

a)

Vì  $A(-5;3)$ thuộc đường thẳng $y=ax+b$ nên tọa độ của $A$ thỏa mãn phương trình này, nghĩa là $3=-5a+b.$

Vì $B\left(\frac{3}{2};-1\right)$ thuộc đường thẳng $y=ax+b$ nên $-1=\frac{3}{2}a+b\iff 3a+2b=-2$

Khi đó $a$ và $b$ là nghiệm của hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}-5a+b=3\\ 3a+2b=-2\end{array}\\ & \iff \{\begin{array}{c}b=3+5a\\ 3a+2\left(3+5a\right)=-2\end{array}\\ & \iff \{\begin{array}{c}b=3+5a\\ 3a+6+10a=-2\end{array}\\ & \iff \{\begin{array}{c}b=3+5a\\ 13a=-8\end{array}\iff \{\begin{array}{c}b=3+5a\\ a=-\frac{8}{13}\end{array}\\ & \iff \{\begin{array}{c}b=-\frac{1}{13}\\ a=-\frac{8}{13}\end{array}\end{array}$

Vậy $a=-\frac{8}{13};b=-\frac{1}{13}.$ 

 b)

Tọa độ giao điểm của hai đường thẳng $(d_1)$: $2x+5y=17,$ 

$(d_2)$:  $4x-10y=14$ 

là nghiệm của hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}2x+5y=17\\ 4x-10y=14\end{array}\iff \{\begin{array}{c}2x+5y=17\\ 2x-5y=7\end{array}\\ & \iff \{\begin{array}{c}x=\frac{7+5y}{2}\\ 2\left(\frac{7+5y}{2}\right)+5y=17\end{array}\\ & \iff \{\begin{array}{c}x=\frac{7+5y}{2}\\ 10y=10\end{array}\\ & \iff \{\begin{array}{c}x=\frac{7+5y}{2}\\ y=1\end{array}\iff \{\begin{array}{c}x=6\\ y=1\end{array}\end{array}$

Do đó giao điểm của $(d_1)$ và$(d_2)$ là  $C(6;1).$

Vì $M(9;-6)$ thuộc đường thẳng $ax–8y=b$ nên $9a+48=b$

Vì $C(6;1)$ thuộc đường thẳng $ax–8y=b$ nên $6a–8=b$

Khi đó $a$ và $b$ là nghiệm của hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}9a+48=b\\ 6a-8=b\end{array}\\ & \iff \{\begin{array}{c}b=6a-8\\ 9a+48=6a-8\end{array}\\ & \iff \{\begin{array}{c}b=6a-8\\ 3a=-56\end{array}\iff \{\begin{array}{c}b=6a-8\\ a=-\frac{56}{3}\end{array}\\ & \iff \{\begin{array}{c}b=-120\\ a=-\frac{56}{3}\end{array}\end{array}$

Vậy $a=-\frac{56}{3};b=-120$.

Bài 21 trang 9 SBT Toán 9 tập 2: Tìm giá trị của m:

a) Để hai đường thẳng$(d_1)$:$5x-2y=3,$ $(d_2)$:  $x+y=m$ cắt nhau tại một điểm trên trục $Oy$. Vẽ hai đường thẳng này trong cùng một mặt phẳng tọa độ.

b) Để hai đường thẳng $(d_1)$: $mx+3y=10$, $(d_2)$: $x-2y=4$ cắt nhau tại một điểm trên trục $Ox$. Vẽ hai đường thẳng này trong cùng  một mặt phẳng tọa độ.

Phương pháp giải:

Sử dụng:

– Hai đường thẳng cắt nhau tại một điểm $A$ trên trục $Oy$ thì $A(0;y).$

– Hai đường thẳng $(d_1)$: $ax+by=c$ và $(d_2)$: $a^{\prime }x+b^{\prime }y=c^{\prime }$ cắt nhau tại điểm $M(x_0;y_0)$  thì tọa độ của $M$ là nghiệm của hệ phương trình: $\{\begin{array}{c}ax+by=c\\ a^{\prime }x+b^{\prime }y=c^{\prime }\end{array}$

– Cặp số $(x_0;y_0)$ là nghiệm của hệ phương trình 

$\{\begin{array}{c}ax+by=c\\ a^{\prime }x+b^{\prime }y=c^{\prime }\end{array}$

$\iff \{\begin{array}{c}a{x}_0+b{y}_0=c\\ a^{\prime }{x}_0+b^{\prime }{y}_0=c^{\prime }\end{array}$

Lời giải:

a)

Vì đường thẳng $(d_1)$: $5x-2y=3,$ 

$(d_2)$: $x+y=m$ cắt nhau tại một điểm trên trục $Oy$ nên giao điểm $A$ của $(d_1)$ và $(d_2)$ có hoành độ bằng $0$, giả sử $A(0;y).$

Khi đó $A(0;y)$ là nghiệm của hệ phương trình:$\{\begin{array}{c}5x-2y=3\\ x+y=m\end{array}$

Thay toạ độ điểm $A$ vào hệ phương trình trên ta được:

$\{\begin{array}{c}5.0-2y=3\\ 0+y=m\end{array}\iff \{\begin{array}{c}y=-\frac{3}{2}\\ m=-\frac{3}{2}\end{array}$ 

Vậy $m=-\frac{3}{2}$ thì $(d_1)$ cắt $(d_2)$ tại một điểm trên trục tung.

– Với $m=-\frac{3}{2}$ ta có $(d_2)$: $x+y=-\frac{3}{2}$$\iff y=-x-\frac{3}{2}$

Cho $x=0\Rightarrow y=-\frac{3}{2}$ ta được $M\left(0;-\frac{3}{2}\right)$

Cho $y=0\Rightarrow x=-\frac{3}{2}$ ta được $N\left(-\frac{3}{2};0\right)$

Đường thẳng $(d_2)$ là đường thẳng đi qua hai điểm $M,N$.

– Vẽ $(d_1)$: $5x-2y=3\iff y=\frac{5}{2}x-\frac{3}{2}$

Cho $x=0\Rightarrow y=-\frac{3}{2}$ ta được $M\left(0;-\frac{3}{2}\right)$

Cho $y=0\Rightarrow x=\frac{3}{5}$ ta được $P\left(\frac{3}{5};0\right)$

Đường thẳng $(d_1)$ là đường thẳng đi qua hai điểm $M,P$.

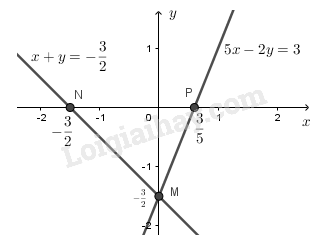
b)

Vì đường thẳng $(d_1)$: $mx+3y=10$ và đường thẳng $(d_2)$: $x–2y=4$ cắt nhau tại một điểm trên trục hoành nên giao điểm $B$ của $(d_1)$ và $(d_2)$ có tung độ bằng $0$, giả sử $B(x;0)$

Khi đó $B(x;0)$ là nghiệm của hệ phương trình:$\{\begin{array}{c}mx+3y=10\\ x–2y=4\end{array}$

Thay toạ độ điểm $B$ vào hệ phương trình trên ta được:

$\begin{array}{rl}& \{\begin{array}{c}mx+3.0=10\\ x-2.0=4\end{array}\iff \{\begin{array}{c}mx=10\\ x=4\end{array}\\ & \iff \{\begin{array}{c}m=\frac{10}{x}\\ x=4\end{array}\\ & \iff \{\begin{array}{c}m=\frac{5}{2}\\ x=4\end{array}\end{array}$ 

Vậy $m=\frac{5}{2}$ thì $(d_1)$ cắt $(d_2)$ tại một điểm trên trục hoành.

– Với $m=\frac{5}{2}$  ta có $(d_1)$: $\frac{5}{2}x+3y=10$$\iff y=-\frac{5}{6}x+\frac{10}{3}$

Cho  $x=0\Rightarrow y=\frac{10}{3}$ ta được $C\left(0;\frac{10}{3}\right)$

Cho $y=0\Rightarrow x=4$ ta được $D\left(4;0\right)$

Đường thẳng $(d_1)$ là đường thẳng đi qua hai điểm $C,D$.

– Vẽ $\left(d_2\right):x-2y=4\iff y=\frac{1}{2}x-2$

Cho $x=0\Rightarrow y=-2$ ta được $E\left(0;-2\right)$

Cho $y=0\Rightarrow x=4$ ta được $D\left(4;0\right)$.

Đường thẳng $(d_2)$ là đường thẳng đi qua hai điểm $E,D$.

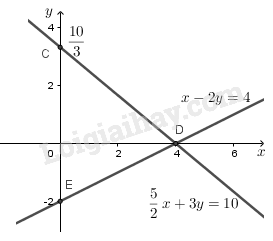
Bài 22 trang 10 SBT Toán 9 tập 2: Tìm giao điểm của hai đường thẳng:

a) $\left(d_1\right):5x-2y=c$ và $\left(d_2\right):x+by=2,$ biết rằng $(d_1)$ đi qua điểm $A(5;-1)$ và $(d_2)$ đi qua điểm $B(-7;3);$

b) $\left(d_1\right):ax+2y=-3$ và $\left(d_2\right):3x-by=5,$ biết rằng $(d_1)$ đi qua điểm $M(3;9)$ và $(d_2)$ đi qua điểm $N(-1;2).$

Phương pháp giải:

Sử dụng:

– Đường thẳng $ax+by=c$ đi qua điểm $M(x_0;y_0)$ $\iff a{x}_0+b{y}_0=c$.

– Hai đường thẳng $(d_1)$: $ax+by=c$ và $(d_2)$: $a^{\prime }x+b^{\prime }y=c^{\prime }$ cắt nhau tại điểm $M$  thì tọa độ của $M$ là nghiệm của hệ phương trình: $\{\begin{array}{c}ax+by=c\\ a^{\prime }x+b^{\prime }y=c^{\prime }\end{array}$

– Cách giải hệ phương trình bằng phương pháp thế:

+ Bước $1$: Rút $x$ hoặc $y$ từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn.

+ Bước $2$: Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.

Lời giải:

a)

Vì $(d_1)$: $5x-2y=c$ đi qua điểm $A(5;-1)$ nên 

$5.5-2.\left(-1\right)=c\iff c=27.$

Khi đó phương trình đường thẳng $(d_1)$: $5x-2y=27$

Vì $\left(d_2\right):x+by=2$ đi qua điểm $B(-7;3)$ nên 

$-7+3b=2\iff 3b=9\iff b=3$

Khi đó phương trình đường thẳng $\left(d_2\right):x+3y=2$

Tọa độ giao điểm của $(d_1)$ và $(d_2)$ là nghiệm của hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}5x-2y=27\\ x+3y=2\end{array}\\ & \iff \{\begin{array}{c}x=2-3y\\ 5\left(2-3y\right)-2y=27\end{array}\\ & \iff \{\begin{array}{c}x=2-3y\\ 10-15y-2y=27\end{array}\\ & \iff \{\begin{array}{c}x=2-3y\\ -17y=17\end{array}\\ & \iff \{\begin{array}{c}x=2-3y\\ y=-1\end{array}\iff \{\begin{array}{c}x=5\\ y=-1\end{array}\end{array}$

Vậy tọa độ giao điểm của $(d_1)$ và $(d_2)$ là $(5;-1)$

 b)

Vì $\left(d_1\right):ax+2y=-3$ đi qua điểm $M(3;9)$ nên$a.3+2.9=-3\iff 3a=-21\iff a=-7$

Khi đó phương trình đường thẳng $\left(d_1\right):-7x+2y=-3$

Vì $\left(d_2\right):3x-by=5$ đi qua điểm $N(-1;2)$ nên$3.\left(-1\right)-b.2=5\iff -2b=8\iff b=-4$

Khi đó phương trình đường thẳng $\left(d_2\right):3x+4y=5$

Tọa độ giao điểm của $(d_1)$và $(d_2)$ là nghiệm của hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}-7x+2y=-3\\ 3x+4y=5\end{array}\\ & \iff \{\begin{array}{c}y=\frac{7x-3}{2}\\ 3x+4.\frac{7x-3}{2}=5\end{array}\\ & \iff \{\begin{array}{c}y=\frac{7x-3}{2}\\ 17x=11\end{array}\iff \{\begin{array}{c}y=\frac{7x-3}{2}\\ x=\frac{11}{17}\end{array}\\ & \iff \{\begin{array}{c}x=\frac{11}{17}\\ y=\frac{13}{17}\end{array}\end{array}$

Vậy tọa độ giao điểm của $(d_1)$và $(d_2)$ là $\left(\frac{11}{17};\frac{13}{17}\right)$.

Bài 23 trang 10 SBT Toán 9 tập 2: Giải các hệ phương trình:

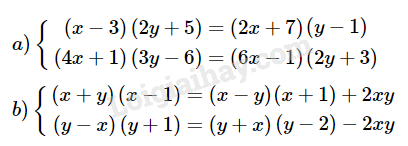
Phương pháp giải:

Sử dụng:

– Cách giải hệ phương trình bằng phương pháp thế:

+ Bước $1$: Rút $x$ hoặc $y$ từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn.

+ Bước $2$: Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.

Lời giải:

$a)$

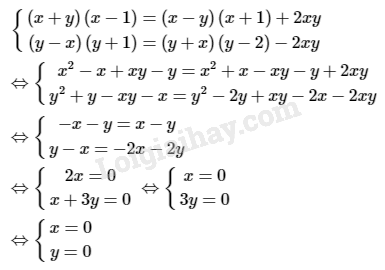
Vậy hệ phương trình có nghiệm duy nhất là: $\left(x;y\right)=\left(-\frac{79}{511};-\frac{51}{73}\right)$

$b)$

Vậy hệ phương trình có nghiệm duy nhất là: $\left(x;y\right)=\left(0;0\right)$.

Bài 24 trang 10 SBT Toán 9 tập 2: Giải các hệ phương trình sau bằng cách đặt ẩn số phụ:

a) $\{\begin{array}{c}\frac{1}{x}+\frac{1}{y}=\frac{4}{5}\\ \frac{1}{x}-\frac{1}{y}=\frac{1}{5}\end{array}$

b) $\{\begin{array}{c}\frac{15}{x}-\frac{7}{y}=9\\ \frac{4}{x}+\frac{9}{y}=35\end{array}$

c) $\{\begin{array}{c}\frac{1}{x+y}+\frac{1}{x-y}=\frac{5}{8}\\ \frac{1}{x+y}-\frac{1}{x-y}=-\frac{3}{8}\end{array}$

d) $\{\begin{array}{c}\frac{4}{2x-3y}+\frac{5}{3x+y}=-2\\ \frac{3}{3x+y}-\frac{5}{2x-3y}=21\end{array}$

e) $\{\begin{array}{c}\frac{7}{x-y+2}-\frac{5}{x+y-1}=4,5\\ \frac{3}{x-y+2}+\frac{2}{x+y-1}=4\end{array}$

Phương pháp giải:

Sử dụng:

– Cách giải hệ phương trình bằng phương pháp đặt ẩn số phụ:

+ Bước 1: Đặt điều kiện để hệ có nghĩa

+ Bước 2: Đặt ẩn phụ và điều kiện của ẩn phụ

+ Bước 3: Giải hệ theo các ẩn phụ đã đặt (sử dụng phương pháp thế)

+ Bước 4: Trở lại ẩn ban đầu để tìm nghiệm của hệ.

Lời giải:

a)

Điều kiện: $x\ne 0;y\ne 0.$

Đặt $\frac{1}{x}=a;\frac{1}{y}=b$ $(a\ne 0;b\ne 0)$

Khi đó hệ phương trình đã cho trở thành:

$\begin{array}{rl}& \{\begin{array}{c}a+b=\frac{4}{5}\\ a-b=\frac{1}{5}\end{array}\iff \{\begin{array}{c}a=b+\frac{1}{5}\\ a+b=\frac{4}{5}\end{array}\\ & \iff \{\begin{array}{c}a=b+\frac{1}{5}\\ b+\frac{1}{5}+b=\frac{4}{5}\end{array}\\ & \iff \{\begin{array}{c}a=b+\frac{1}{5}\\ 2b=\frac{3}{5}\end{array}\iff \{\begin{array}{c}a=b+\frac{1}{5}\\ b=\frac{3}{10}\end{array}\\ & \iff \{\begin{array}{c}a=\frac{1}{2}\\ b=\frac{3}{10}\end{array}\text{(thoả mãn)}\end{array}$ 

Suy ra: 

$\{\begin{array}{c}\frac{1}{x}=\frac{1}{2}\\ \frac{1}{y}=\frac{3}{10}\end{array}\iff \{\begin{array}{c}x=2\\ y=\frac{10}{3}\end{array}\text{(thoả mãn)}$

Vậy hệ phương trình đã cho có nghiệm duy nhất là $\left(x;y\right)=\left(2;\frac{10}{3}\right)$

b)

Điều kiện: $x\ne 0;y\ne 0$

Đặt $\frac{1}{x}=a;\frac{1}{y}=b$ $(a\ne 0;b\ne 0)$

Khi đó hệ phương trình đã cho trở thành:

$\begin{array}{rl}& \{\begin{array}{c}15a-7b=9\\ 4a+9b=35\end{array}\\ & \iff \{\begin{array}{c}b=\frac{15a-9}{7}\\ 4a+9b=35\end{array}\\ & \iff \{\begin{array}{c}b=\frac{15a-9}{7}\\ 4a+9.\frac{15a-9}{7}=35\end{array}\\ & \iff \{\begin{array}{c}b=\frac{15a-9}{7}\\ 28a+135a-81=245\end{array}\\ & \iff \{\begin{array}{c}b=\frac{15a-9}{7}\\ 163a=326\end{array}\\ & \iff \{\begin{array}{c}b=\frac{15a-9}{7}\\ a=2\end{array}\\ & \iff \{\begin{array}{c}b=3\\ a=2\end{array}\text{(thoả mãn)}\end{array}$ 

Suy ra: 

$\{\begin{array}{c}\frac{1}{x}=2\\ \frac{1}{y}=3\end{array}\iff \{\begin{array}{c}x=\frac{1}{2}\\ y=\frac{1}{3}\end{array}\text{(thoả mãn)}$

Vậy hệ phương trình đã cho có nghiệm duy nhất là $(x;y)$ = $\left(\frac{1}{2};\frac{1}{3}\right)$

 c)

Điều kiện: $x\ne \pm y$. Đặt $\frac{1}{x+y}=a;\frac{1}{x-y}=b$ $(a\ne 0;b\ne 0)$

Khi đó hệ phương trình đã cho trở thành: 

$\begin{array}{rl}& \{\begin{array}{c}a+b=\frac{5}{8}\\ a-b=-\frac{3}{8}\end{array}\iff \{\begin{array}{c}a=b-\frac{3}{8}\\ a+b=\frac{5}{8}\end{array}\\ & \iff \{\begin{array}{c}a=b-\frac{3}{8}\\ b-\frac{3}{8}+b=\frac{5}{8}\end{array}\\ & \iff \{\begin{array}{c}a=b-\frac{3}{8}\\ b=\frac{1}{2}\end{array}\\ & \iff \{\begin{array}{c}a=\frac{1}{8}\\ b=\frac{1}{2}\end{array}\text{(thoả mãn)}\end{array}$ 

Suy ra:

$\begin{array}{rl}& \{\begin{array}{c}\frac{1}{x+y}=\frac{1}{8}\\ \frac{1}{x-y}=\frac{1}{2}\end{array}\iff \{\begin{array}{c}x+y=8\\ x-y=2\end{array}\\ & \iff \{\begin{array}{c}x=y+2\\ y+2+y=8\end{array}\iff \{\begin{array}{c}x=y+2\\ 2y=6\end{array}\\ & \iff \{\begin{array}{c}x=y+2\\ y=3\end{array}\\ & \iff \{\begin{array}{c}x=5\\ y=3\end{array}\text{(thoả mãn)}\end{array}$

Vậy hệ phương trình đã cho có nghiệm duy nhất là $(x;y)=(5;3).$

 d)

Điều kiện: $x\ne \frac{3}{2}y;x\ne -\frac{1}{3}y.$ Đặt $\frac{1}{2x-3y}=a;\frac{1}{3x+y}=b$ 

$(a\ne 0;b\ne 0)$

Khi đó hệ phương trình đã cho trở thành:

$\begin{array}{rl}& \{\begin{array}{c}4a+5b=-2\\ 3b-5a=21\end{array}\\ & \iff \{\begin{array}{c}b=\frac{5a+21}{3}\\ 4a+5b=-2\end{array}\\ & \iff \{\begin{array}{c}b=\frac{5a+21}{3}\\ 4a+5.\frac{5a+21}{3}=-2\end{array}\\ & \iff \{\begin{array}{c}b=\frac{5a+21}{3}\\ 12a+25a+105=-6\end{array}\\ & \iff \{\begin{array}{c}b=\frac{5a+21}{3}\\ 37a=-111\end{array}\\ & \iff \{\begin{array}{c}b=\frac{5a+21}{3}\\ a=-3\end{array}\\ & \iff \{\begin{array}{c}b=2\\ a=-3\end{array}\text{(thoả mãn)}\end{array}$

Suy ra:

$\begin{array}{rl}& \{\begin{array}{c}\frac{1}{2x-3y}=-3\\ \frac{1}{3x+y}=2\end{array}\\ & \iff \{\begin{array}{c}2x-3y=-\frac{1}{3}\\ 3x+y=\frac{1}{2}\end{array}\\ & \iff \{\begin{array}{c}y=\frac{1}{2}-3x\\ 2x-3\left(\frac{1}{2}-3x\right)=\frac{-1}{3}\end{array}\\ & \iff \{\begin{array}{c}y=\frac{1}{2}-3x\\ 2x+9x=-\frac{1}{3}+\frac{3}{2}\end{array}\\ & \iff \{\begin{array}{c}y=\frac{1}{2}-3x\\ 11x=\frac{7}{6}\end{array}\\ & \iff \{\begin{array}{c}y=\frac{1}{2}-3x\\ x=\frac{7}{66}\end{array}\\ & \iff \{\begin{array}{c}y=\frac{1}{2}-\frac{7}{22}\\ x=\frac{7}{66}\end{array}\\ & \iff \{\begin{array}{c}y=\frac{2}{11}\\ x=\frac{7}{66}\end{array}\text{(thoả mãn)}\end{array}$

Vậy hệ phương trình đã cho có nghiệm duy nhất là$(x;y)=\left(\frac{7}{66};\frac{2}{11}\right)$

 e)

Điều kiện:$x-y+2\ne 0;x+y-1\ne 0.$

Đặt $\frac{1}{x-y+2}=a;\frac{1}{x+y-1}=b.$ 

$(a\ne 0;b\ne 0)$

Khi đó hệ phương trình đã cho trở thành: 

$\begin{array}{rl}& \{\begin{array}{c}7a-5b=4,5\\ 3a+2b=4\end{array}\\ & \iff \{\begin{array}{c}b=\frac{4-3a}{2}\\ 7a-5b=4,5\end{array}\\ & \iff \{\begin{array}{c}b=\frac{4-3a}{2}\\ 7a-5.\frac{4-3a}{2}=4,5\end{array}\\ & \iff \{\begin{array}{c}b=\frac{4-3a}{2}\\ 14a-20+15a=9\end{array}\\ & \iff \{\begin{array}{c}b=\frac{4-3a}{2}\\ 29a=29\end{array}\\ & \iff \{\begin{array}{c}b=\frac{4-3a}{2}\\ a=1\end{array}\\ & \iff \{\begin{array}{c}b=\frac{1}{2}\\ a=1\end{array}\text{(thoả mãn)}\\ & \Rightarrow \{\begin{array}{c}\frac{1}{x-y+2}=1\\ \frac{1}{x+y-1}=\frac{1}{2}\end{array}\\ & \iff \{\begin{array}{c}x-y+2=1\\ x+y-1=2\end{array}\\ & \iff \{\begin{array}{c}x=y-1\\ y-1+y-1=2\end{array}\\ & \iff \{\begin{array}{c}x=y-1\\ 2y=4\end{array}\\ & \iff \{\begin{array}{c}x=y-1\\ y=2\end{array}\\ & \iff \{\begin{array}{c}x=1\\ y=2\end{array}\text{(thoả mãn)}\end{array}$

Vậy hệ phương trình đã cho có nghiệm duy nhất là $(x;y)=(1;2).$

Bài tập bổ sung (trang 10 SBT Toán 9)

Bài 3.1 trang 10 SBT Toán 9 tập 2: Tìm $a$ và $b$ để hệ

$\{\begin{array}{c}ax+by=17\\ 3bx+ay=-29\end{array}$

có nghiệm là $(x;y)=(1;-4)$

Phương pháp giải:

Sử dụng:

– Cặp số $(x_0;y_0)$ là nghiệm của hệ phương trình 

$\{\begin{array}{c}ax+by=c\\ a^{\prime }x+b^{\prime }y=c^{\prime }\end{array}$

$\iff \{\begin{array}{c}a{x}_0+b{y}_0=c\\ a^{\prime }{x}_0+b^{\prime }{y}_0=c^{\prime }\end{array}$

– Cách giải hệ phương trình bằng phương pháp thế (coi $a,b$ là ẩn):

+ Bước 1: Rút $a$ hoặc $b$ từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn.

+ Bước 2: Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.

Lời giải:

Để $(x;y)=(1;-4)$ là nghiệm của hệ phương trình đã cho, ta thay $x=1;$$y=-4$ vào hệ phương trình ta có:

$\begin{array}{rl}& \{\begin{array}{c}a-4b=17\\ 3b-4a=-29\end{array}\\ & \iff \{\begin{array}{c}a=4b+17\\ 3b-4\left(4b+17\right)=-29\end{array}\\ & \iff \{\begin{array}{c}a=4b+17\\ 3b-16b-68=-29\end{array}\\ & \iff \{\begin{array}{c}a=4b+17\\ -13b=39\end{array}\\ & \iff \{\begin{array}{c}a=4b+17\\ b=-3\end{array}\\ & \iff \{\begin{array}{c}a=5\\ b=-3\end{array}\end{array}$

Vậy $a=5;b=-3.$

Bài 3.2 trang 10 SBT Toán 9 tập 2: Giải hệ phương trình:

$\{\begin{array}{c}2x-y=5\\ \left(x+y+2\right)\left(x+2y-5\right)=0\end{array}$

Phương pháp giải:

Sử dụng:

– Cách giải phương trình tích: 

$A(x).B(x)=0\iff [\begin{array}{c}A(x)=0\\ B(x)=0\end{array}$

– Cách giải hệ phương trình bằng phương pháp thế :

+ Bước 1: Rút $x$ hoặc $y$ từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn.

+ Bước 2: Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.

Lời giải:

Ta có

$(x+y+2)(x+2y-5)=0\iff [\begin{array}{c}x+y+2=0\\ x+2y-5=0\end{array}$

Khi đó ta có thể viết hệ đã cho thành hai hệ phương trình:

$\{\begin{array}{c}2x-y=5\\ x+y+2=0\end{array}$

hoặc

$\{\begin{array}{c}2x-y=5\\ x+2y-5=0\end{array}$

Giải hệ:

$\{\begin{array}{c}2x-y=5\\ x+y+2=0\end{array}\iff \{\begin{array}{c}y=2x-5\\ x+2x-5+2=0\end{array}$

$\begin{array}{rl}& \iff \{\begin{array}{c}y=2x-5\\ 3x-3=0\end{array}\\ & \iff \{\begin{array}{c}y=2x-5\\ x=1\end{array}\\ & \iff \{\begin{array}{c}y=-3\\ x=1\end{array}\end{array}$

Giải hệ:

$\{\begin{array}{c}2x-y=5\\ x+2y-5=0\end{array}\iff \{\begin{array}{c}y=2x-5\\ x+2\left(2x-5\right)-5=0\end{array}$

$\begin{array}{rl}& \iff \{\begin{array}{c}y=2x-5\\ 5x-15=0\end{array}\\ & \iff \{\begin{array}{c}y=2x-5\\ x=3\end{array}\\ & \iff \{\begin{array}{c}y=1\\ x=3\end{array}\end{array}$

Vậy hệ phương trình đã cho có hai nghiệm:

$\left(x_1;y_1\right)=\left(1;-3\right)$ ; $\left(x_2;y_2\right)=\left(3;1\right)$.