Giải SBT Toán lớp 7 Bài tập cuối chương 3
Giải trang 64 Tập 1
Bài 1 trang 64 Sách bài tập Toán 7 Tập 1: Điền vào chỗ chấm. Hình hộp chữ nhật (hình lập phương) có:
……. cạnh; ……. mặt; ……. đỉnh; ………. đường chéo; mỗi đỉnh có ……. góc.
Lời giải
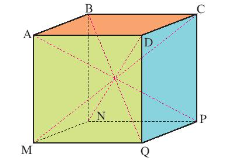
Ta điền được như sau:
Hình hộp chữ nhật (hình lập phương) có:
12 cạnh; 6 mặt; 8 đỉnh; 4 đường chéo; mỗi đỉnh có 3 góc.
Bài 2 trang 64 Sách bài tập Toán 7 Tập 1: Cho hình hộp chữ nhật ABCD.EFGH.
a) Hãy nêu các mặt chứa cạnh EF.
b) Cạnh GH bằng cách cạnh nào?
c) Vẽ đường chéo xuất phát từ đỉnh E, G.
Lời giải
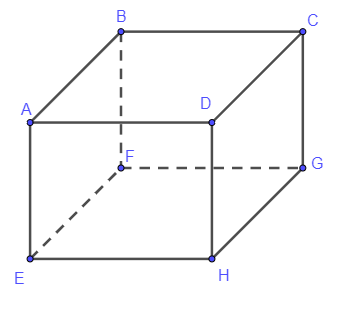
Quan sát hình hộp chứ nhật ABCD.EFGH, ta có:
a) Các mặt chứa cạnh EF là: mặt ABFE, mặt EFGH.
b) Các cạnh bằng cạnh GH là: EF, CD, AB (ta có thể viết GH = EF = CD = AB).
c) Đường chéo xuất phát từ đỉnh E là EC, đường chéo xuất phát từ đỉnh G là GA.
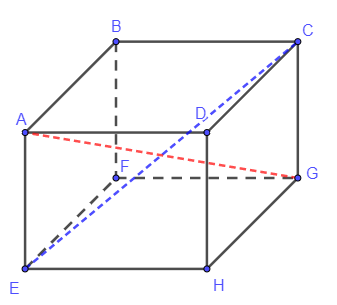
Bài 3 trang 64 Sách bài tập Toán 7 Tập 1: Bạn Nam dự định dùng thanh sắt cắt ra để làm một cái khung hình lập phương cạnh 30 cm. Hỏi thanh sắt dài 3,5 m có đủ để làm cái khung không?
Lời giải
Hình lập phương có 12 cạnh bằng nhau, mỗi cạnh 30 cm.
Do đó độ dài tất cả các cạnh là: 12 . 30 = 360 (cm).
Đổi 360 cm = 3,6 m.
Mà 3,5 m < 3,6 m.
Vậy thanh sắt không đủ dài để làm khung.
Bài 4 trang 64 Sách bài tập Toán 7 Tập 1: Người ta cần làm một chiếc hộp hình hộp chữ nhật có kích thước 2 cm, 3 cm và 5 cm.
a) Hãy chỉ ra hai cách cắt tấm bìa để gấp thành hình hộp trên.
b) Hãy tính diện tích của tấm bìa sau khi cắt trong mỗi trường hợp.
Lời giải
a)
Cách 1: Trên tấm bìa, vẽ 2 hình chữ nhật với các kích thước như hình dưới, rồi gấp theo các đường nét đứt ta được hình hộp chữ nhật thỏa mãn.
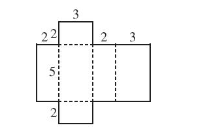
Cách 2: Trên tấm bìa, vẽ 2 hình chữ nhật với các kích thước như hình dưới, rồi gấp theo các đường nét đứt ta được hình hộp chữ nhật thảo mãn.
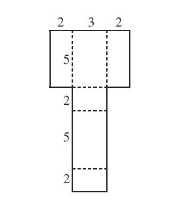
b) Diện tích các tấm bìa sau khi cắt ở 2 cách trên đều bằng diện tích toàn phần của hình hộp chữ nhật nên diện tích tấm bìa sau khi cắt ở Cách 1 bằng diện tích tấm bìa sau khi cắt ở Cách 2 và là: S = 2 . (2 . 3 + 2 . 5 + 3 . 5) = 62 (cm2).
Bài 5 trang 64 Sách bài tập Toán 7 Tập 1:Từ một tấm bìa hình chữ nhật, hãy chỉ ra hai cách cắt và gấp để tạo thành một hình lăng trụ đứng có đáy là tam giác đều cạnh 3 cm và chiều cao 2 cm.
Lời giải
Cách 1: Trên tấm bìa, ta vẽ hai hình tam giác đều cạnh 3 cm và 3 hình chữ nhật bằng nhau với các kích thước như trên hình vẽ rồi gấp theo các đường nét đứt ta được hình lăng trụ đứng thỏa mãn yêu cầu.
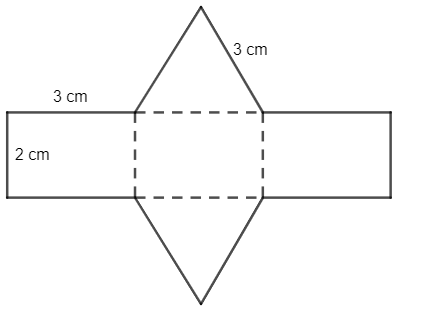
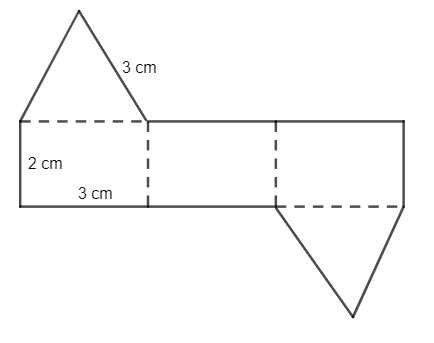
Cách 2: Trên tấm bìa, ta vẽ hai hình tam giác đều cạnh 3 cm và 3 hình chữ nhật bằng nhau với các kích thước như trên hình vẽ rồi gấp theo các đường nét đứt ta được hình lăng trụ đứng thỏa mãn yêu cầu.
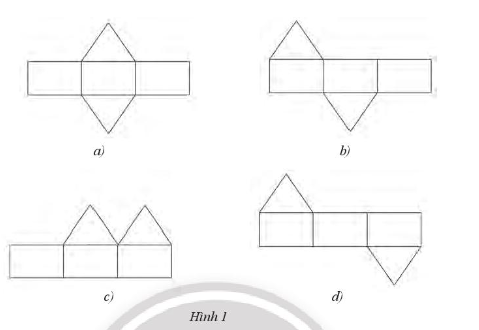
Bài 6 trang 64 Sách bài tập Toán 7 Tập 1: Trong bốn tấm bìa dưới đây, tấm nào không thể gấp thành hình lăng trụ đứng tam giác?
Lời giải
– Theo Bài 5, ta thấy tấm bìa ở Hình 1a) và Hình 1d) có thể gấp được thành hình lăng trụ đứng tam giác.
– Ta gấp tấm bìa Hình 1b) theo các đường nét đứt như hình dưới đây, ta được hình lăng trụ đứng tam giác.
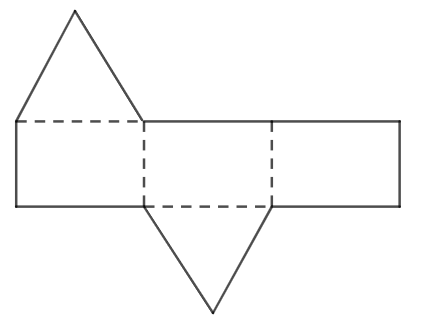
– Ở tấm bìa Hình 1c), hai phần tam giác ở cùng phía, do đó ta không thể gấp để tạo thành 2 đáy của lăng trụ đứng tam giác (do hai đáy của hình lăng trụ đứng tam giác phải song song với nhau).
Vậy tấm bìa Hình 1c) không thể gấp được thành hình lăng trụ đứng tam giác.
Giải trang 65 Tập 1
Bài 7 trang 65 Sách bài tập Toán 7 Tập 1: Một khối kim loại có dạng hình lăng trụ đứng đáy tam giác vuông có kích thước hai cạnh góc vuông là 3 cm, 4 cm, cạnh huyền 5 cm. Người ta khoét một lỗ hình lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 2 cm, 1,5 cm, cạnh huyền 2,5 cm (Hình 2). Tính thể tích của khối kim loại (không tính cái lỗ).

Lời giải
+ Khối kim loại có dạng hình lăng trụ đứng tam giác với đáy là tam giác vuông có kích thước hai cạnh góc vuông là 3 cm, 4 cm và chiều cao của lăng trụ là h = 4,5 cm.
Khi đó, thể tích của khối kim loại (bao gồm cái lỗ) là:
V = Sđ . h = (. 3 . 4) . 4,5 = 27 (cm3).
+ Cái lỗ khoét có dạng hình lăng trụ đứng tam giác với đáy là tam giác vuông có kích thước hai cạnh góc vuông là 2 cm, 1,5 cm và chiều cao của lăng trụ là h = 4,5 cm (bằng chiều cao của khối lăng trụ kim loại).
Khi đó, thể tích của cái lỗ là:
v = Sđn . h = ( . 2 . 1,5) . 4,5 = 6,75 (cm3).
Vậy thể tích của khối kim loại (không tính cái lỗ) là: 27 – 6,75 = 20,25 (cm3).
Bài 8 trang 65 Sách bài tập Toán 7 Tập 1: Gạch đặc nung (Hình 3) là loại gạch được làm bằng đất sét và được nung nguyên khối, không có lỗ rỗng. Do kết cấu khối đặc vậy nên khối gạch khá cứng chắc, ít thấm nước, đảm bảo kết cấu công trình. Bác Ba muốn làm 500 viên gạch như thế, hỏi cần bao nhiêu mét khối đất sét? Biết kích thước mỗi viên gạch là 205 mm, 95 mm, 55 mm, và độ dãn nở không đáng kể.
Lời giải
Thể tích của một viên gạch nung là: 205 . 95 . 55 = 1 071 125 (mm3).
Thể tích của khối đất sét cần dùng để làm 500 viên gạch nung là:
500 . 1 071 125 = 535 562 500 (mm3).
Đổi 535 562 500 mm3 = 0,5355625 m3 ≈ 0,54 m3.
Vậy cần khoảng 0,54 mét khối đất sét để làm 500 viên gạch.
Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác
Bài tập cuối chương 3
Bài 1: Các góc ở vị trí đặc biệt
Bài 2: Tia phân giác
Bài 3: Hai đường thẳng song song
====== ****&**** =====