Sách bài tập Toán 11 Bài 5 (Cánh diều): Hình lăng trụ và hình hộp

Giải SBT Toán 11 Bài 5: Hình lăng trụ và hình hộp

Bài 36 trang 112 SBT Toán 11: Số đường chéo trong một hình hộp là:

A. 4.

B. 24.

C. 28.

D. 2.

Lời giải:

Đáp án đúng là: A

Hình hộp có 4 đường chéo.

Bài 37 trang 112 SBT Toán 11: Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của BC, B’C’. Khẳng định nào sau đây là đúng?

A. (A’MN) // (ACC’).

B. (A’BN) // (AC’M).

C. C’M // (A’B’B).

D. BN // (ACC’A’).

Lời giải:

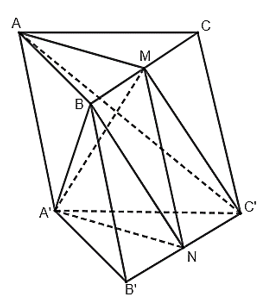
+ Vì A, C, C’, A’ đồng phẳng nên A’ ∈ (ACC’), mà A’ ∈ (A’MN) nên hai mặt phẳng (A’MN) và (ACC’) không thể song song. Do đó đáp án A sai.

+ Trong mặt phẳng (BCC’B’), hai đường thẳng C’M và BB’ cắt nhau nên C’M không thể song song với mặt phẳng (A’B’B). Do đó đáp án C sai.

+ Trong hình bình hành BCC’B’ có M, N lần lượt là trung điểm của BC, B’C’ nên ta chứng minh được MN // BB’ và MN = BB’.

Mà AA’ // BB’ và AA’ = BB’ nên MN // AA’ và MN = AA’.

Suy ra AMNA’ là hình bình hành, do đó AM // A’N.

Mà A’N ⊂ (A’BN) nên AM // (A’BN). (1)

Ta cũng chứng minh được BMC’N là hình bình hành nên C’M // BN.

Mà BN ⊂ (A’BN) nên C’M // (A’BN). (2)

Từ (1) và (2) suy ra (A’BN) // (AC’M). Vậy đáp án B đúng.

Bài 38 trang 112 SBT Toán 11: Cho hình hộp ABCD.A’B’C’D’. Khẳng định nào sau đây là sai?

A. Các mặt của hình hộp là các hình bình hành.

B. Hai mặt phẳng lần lượt chứa hai mặt đối diện của hình hộp song song với nhau.

C. Các đoạn thẳng AC’, A’C, BD’, B’D bằng nhau.

D. Các đường thẳng AC’, A’C, BD’, B’D đồng quy.

Lời giải:

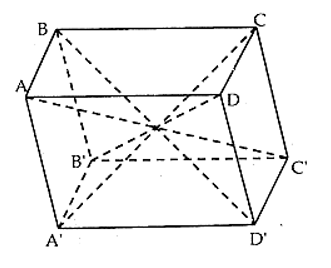
Theo định nghĩa và tính chất của hình hộp, ta có các đáp án A, B, D đúng và đáp án C sai.

Bài 39 trang 113 SBT Toán 11: Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của A’B’, B’C’. Gọi d là giao tuyến của hai mặt phẳng (BMN) và (ACC’A’). Khẳng định nào sau đây là đúng?

A. d // AA’.

B. d // BC.

C. d // A’B’.

D. d // A’C’.

Lời giải:

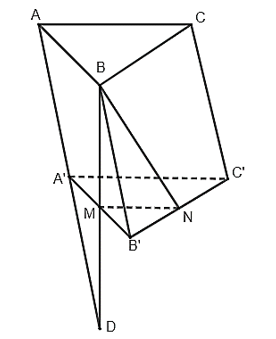
Vì M, N lần lượt là trung điểm của A’B’, B’C’ nên MN là đường trung bình của tam giác A’B’C’, suy ra MN // A’C’.

Trong mặt phẳng (ABB’A’), gọi D là giao điểm của AA’ và BM.

Vì AA’ ⊂ (ACC’A’) nên D ∈ (ACC’A’), BM ⊂ (BMN) nên D ∈ (BMN).

Khi đó, hai mặt phẳng (BMN), (ACC’A’) có điểm chung là D và lần lượt chứa hai đường thẳng MN và A’C’ song song với nhau nên giao tuyến của chúng là đường thẳng d đi qua điểm D và song song với MN, A’C’.

Bài 40 trang 113 SBT Toán 11: Cho hình hộp ABCD.A’B’C’D’. Mặt phẳng (BA’C’) song song với mặt phẳng nào dưới đây?

A. (ACD).

B. (ADD’).

C. (DCD’).

D. (AD’C).

Lời giải:

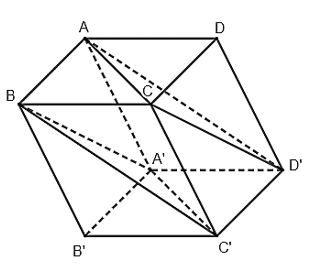
Do AA’B’B và CDD’C là các hình bình hành nên AB // C’D’ và AB = C’D’ (cùng song song và bằng CD).

Suy ra ABC’D’ là hình bình hành. Do đó, AD’ // BC’.

Mà BC’ ⊂ (BA’C’) nên AD’ // (BA’C’). (1)

Tương tự, A’BCD’ cũng là hình bình hành nên A’B // CD’.

Mà A’B ⊂ (BA’C’) nên CD’ // (BA’C’). (2)

Từ (1) và (2) suy ra (AD’C) // (BA’C’).

Bài 41 trang 113 SBT Toán 11: Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M là trung điểm của A’C’.

a) Chứng minh rằng A’B // (B’CM).

b) Xác định giao tuyến d của hai mặt phẳng (ABC) và (A’BC’).

Lời giải:

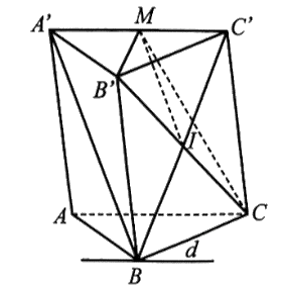
a) Gọi I là giao điểm của BC và B’C.

Do tứ giác BCC’B’ là hình bình hành nên I là trung điểm của BC’.

Do đó MI là đường trung bình của tam giác A’C’B, suy ra MI // A’B.

Mặt khác, MI ⊂ (B’CM) nên A’B // (B’CM).

b) Hai mặt phẳng (ABC) và (A’BC’) có điểm chung là B và lần lượt chứa hai đường thẳng song song là AC, A’C’ nên giao tuyến của chúng là đường thẳng d đi qua B và song song với AC.

Bài 42 trang 113 SBT Toán 11: Cho hình hộp ABCD.A’B’C’D’. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CC’, C’D’, D’A’, AA’. Chứng minh rằng:

a) Sáu điểm M, N, P, Q, R, S cùng thuộc một mặt phẳng.

b) Các đoạn thẳng MQ, NR, PS cắt nhau tại trung điểm của mỗi đoạn.

Lời giải:

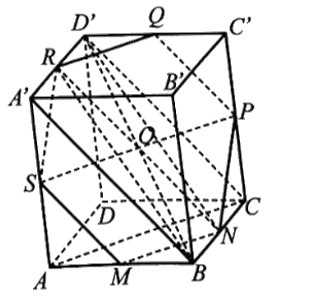
a) Ta có S và P lần lượt là trung điểm của AA’ và CC’.

Suy ra $AS=\frac{1}{2}AA‘;CP=\frac{1}{2}AA‘$.

Mà AA’ = CC’ và AA’ // CC’ (do ABCD.A’B’C’D’ là hình hộp)

Nên AS = CP và AS // CP. Do đó, tứ giác ASPC là hình bình hành.

Suy ra AC // SP.

Mặt khác MN // AC (do MN là đường trung bình của tam giác ABC).

Khi đó, MN // SP.

Vậy M, N, P, S cùng thuộc một mặt phẳng.

Ta cũng chứng minh được PQ // CD’, CD’ // BA’, BA’ // MS nên PQ // MS.

Do đó Q ∈ (MNPS).

Tương tự ta có QR // MN nên R ∈ (MNPS).

Vậy sáu điểm M, N, P, Q, R, S cùng thuộc một mặt phẳng.

b) Gọi O là giao điểm của các đường chéo hình hộp ABCD.A’B’C’D’.

Khi đó, O là trung điểm của các đường chéo BD’, B’D, AC’, A’C.

Ta có tứ giác BND’R là hình bình hành, nên hai đường chéo BD’, NR cắt nhau tại trung điểm O của mỗi đường.

Tương tự, ta chứng minh được QM, PS đều nhận O là trung điểm.

Vậy các đoạn thẳng MQ, NR, PS cắt nhau tại trung điểm của mỗi đoạn.

Bài 43 trang 113 SBT Toán 11: Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G, I, K lần lượt là trọng tâm các tam giác ABC, A’B’C’, A’B’B.

a) Chứng minh rằng IK // (BCC’B’).

b) Chứng minh rằng (AGK) // (A’IC).

c) Gọi (α) là mặt phẳng đi qua điểm K và song song với mặt phẳng (ABC). Mặt phẳng (α) cắt A’C tại điểm L. Tính $\frac{LA‘}{LC}$.

Lời giải:

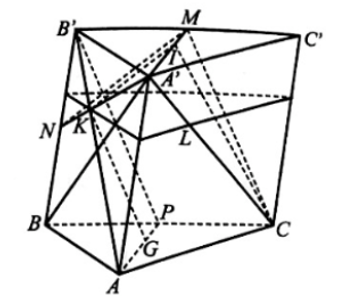
a) Gọi M, N lần lượt là trung điểm của cạnh B’C’, BB’.

Do I, K lần lượt là trọng tâm của các tam giác A’B’C’ và A’B’B nên $\frac{A‘I}{A‘M}=\frac{A‘K}{A‘N}=\frac{2}{3}$.

Suy ra IK // MN. Mà MN ⊂ (BCC’B’) nên IK // (BCC’B’).

b) Gọi P là trung điểm của cạnh BC.

Khi đó, mặt phẳng (AGK) cũng là mặt phẳng (AB’P), mặt phẳng (A’IC) cũng là mặt phẳng (A’MC). 

Ta có B’P // MC (B’MCP là hình bình hành) nên B’P // (A’MC)

AP // A’M (APMA’ là hình bình hành) nên AP // (A’MC).

Từ đó, suy ra (AB’P) // (A’MC) hay (AGK) // (A’IC).

c) Với K là trọng tâm của tam giác A’BB’, ta suy ra $\frac{B‘K}{B‘A}=\frac{1}{3}$ nên $\frac{B‘K}{KA}=\frac{1}{2}$.

Ta có đường thẳng B’A cắt ba mặt phẳng song song (A’B’C’), (α), (ABC) lần lượt tại B’, K, A; đường thẳng A’C cũng cắt ba mặt phẳng trên theo thứ tự tại A’, L, C.

Áp dụng định lí Thalés trong không gian, ta có: $\frac{B‘K}{A‘L}=\frac{KA}{LC}=\frac{AB‘}{CA‘}$.

Suy ra $\frac{A‘L}{LC}=\frac{B‘K}{KA}=\frac{1}{2}$.

Vậy $\frac{LA‘}{LC}=\frac{1}{2}$.

Bài 44 trang 113 SBT Toán 11: Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương của tất cả các cạnh.

Lời giải:

Trước hết ta chứng minh một kết quả trong hình học phẳng: Trong hình bình hành, tổng bình phương của hai đường chéo bằng tổng bình phương tất cả các cạnh.

Xét hình bình hành MNPQ:

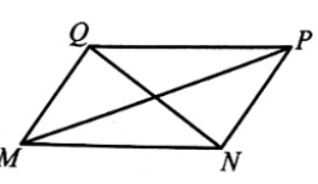
Áp dụng định lí côsin trong các tam giác MPQ và QPN, ta có:

MP2 = QM2 + QP2 – 2QM . QP . cos$\widehat{MQP}$

QN2 = PQ2 + PN2 – 2PQ . PN . cos$\widehat{QPN}$

Do QM = PN và $\cos \widehat{MQP}=-\cos \widehat{QPN}$ (do hai góc bù nhau) nên ta có:

MP2 + QN2 = 2(QM2 + QP2).

Xét hình hộp ABCD.A’B’C’D’:

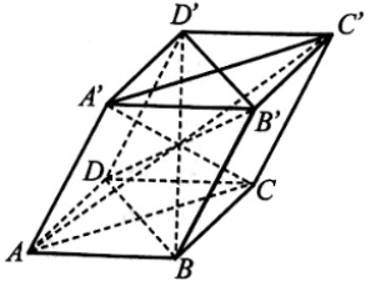
Áp dụng kết quả trên cho hai hình bình hành AA’C’C và BB’D’D ta được:

AC’2 + A’C2 = 2(AA’2 + A’C’2)

BD’2 + B’D2 = 2(BB’2 + B’D’2)

Suy ra AC’2 + A’C2 + BD’2 + B’D2 = 4AA’2 + 2(A’C’2 + B’D’2)    (do AA’ = BB’).

Mặt khác, trong hình bình hành A’B’C’D’, ta có: A’C’2 + B’D’2 = 2(A’B’2 + A’D’2).

Vậy AC’2 + A’C2 + BD’2 + B’D2 = 4AA’2 + 4A’B’2 + 4A’D’2.

Từ đó suy ra điều phải chứng minh.

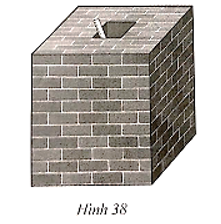
Bài 45 trang 113 SBT Toán 11: Phần trong của một bể đựng nước được xây có dạng hình hộp như Hình 38. Để xác định tỉ số của độ cao mực nước trong bể với chiều cao của lòng bể, bạn Minh làm như sau: “Lấy một thanh thước thẳng đủ dài cắm vào bể sao cho một đầu chạm đáy bể và để thước tựa vào mép dưới của thành miệng bể, đánh dấu điểm tựa. Sau đó rút thước lên, tính tỉ số độ dài của phần thước chìm trong nước và độ dài của phần thước từ điểm được đánh dấu đến điểm đầu chạm đáy bể. Tỉ số đó chính bằng tỉ số của độ cao mực nước trong bể với chiều cao của lòng bể”. Bạn Minh làm có đúng không? Vì sao?

Lời giải:

Bạn Minh làm như vậy là đúng.

Giả sử phần trong bể nước và thước được biểu diễn bởi hình hộp ABCD.A’B’C’D’ và đường thẳng MO. Mặt nước được biểu diễn bởi mặt phẳng (IJKL) (như hình vẽ).

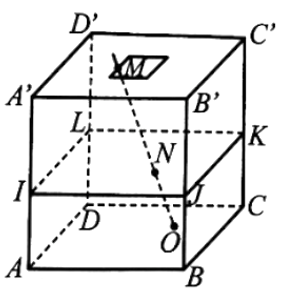
Khi đó ba mặt phẳng (ABCD), (A’B’C’D’), (IJKL) đôi một song song, áp dụng định lí Thalès trong không gian ta có:

$\frac{A‘I}{MN}=\frac{IA}{NO}=\frac{AA‘}{OM}\Rightarrow \frac{IA}{AA‘}=\frac{NO}{OM}$.