Giải SBT Toán 11 Bài 13: Hai mặt phẳng song song
Bài 4.29 trang 67 SBT Toán 11 Tập 1: Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường a, b, c, d đôi một song song và không nằm trong mặt phẳng (ABCD).
a) Chứng minh rằng hai mặt phẳng mp(a,b) và mp(c,d) song song với nhau.
b) Chứng minh rằng hai mặt phẳng mp(a,d) và mp(b,c) song song với nhau.
c) Một mặt phẳng cắt bốn đường thẳng a, b, c, d lần lượt tại A’, B’, C’, D’. Chứng minh rằng tứ giác A’B’C’D’ là hình bình hành.
Lời giải:
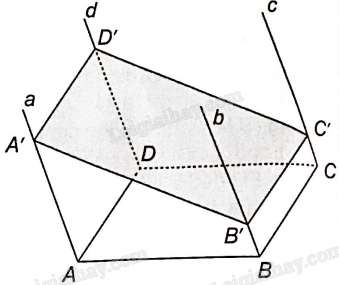
a) Vì a//d nên a//mp(c, d).
Vì ABCD là hình bình hành nên AB//CD, do đó AB// mp(c, d).
Mặt phẳng (a, b) chứa hai đường thẳng a và AB cắt nhau tại A và cùng song song với mp(c, d).
Do đó, hai mặt phẳng mp(a,b) và mp(c,d) song song với nhau.
b) Vì a//b nên a//mp(b, c).
Vì ABCD là hình bình hành nên AD//BC, do đó AD// mp(b, c).
Mặt phẳng (a, d) chứa hai đường thẳng a và AD cắt nhau tại A và cùng song song với mp(b, c).
hai mặt phẳng mp(a,d) và mp(b,c) song song với nhau.
c) Vì mặt phẳng (a, b) song song với mặt phẳng (c, d) nên giao tuyến của mặt phẳng (A’B’C’D’) với hai mặt phẳng đó song song với nhau, tức là A’B’//C’D’.
Vì hai mặt phẳng mp(a,d) và mp(b,c) song song với nhau nên giao tuyến của mặt phẳng (A’B’C’D’) với hai mặt phẳng đó song song với nhau, tức là A’D’//C’B’.
Tứ giác A’B’C’D’ có: A’B’//C’D’, A’D’//C’B’ nên tứ giác A’B’C’D’ là hình bình hành.
Bài 4.30 trang 67 SBT Toán 11 Tập 1: Cho tứ diện ABCD và một điểm O nằm trong tam giác BCD. Gọi (P) là mặt phẳng qua O và song song với mặt phẳng (ABD).
a) Xác định giao tuyến của mặt phẳng (P) và mặt phẳng (BCD).
b) Xác định giao tuyến của mặt phẳng (P) và các mặt còn lại của tứ diện.
Lời giải:
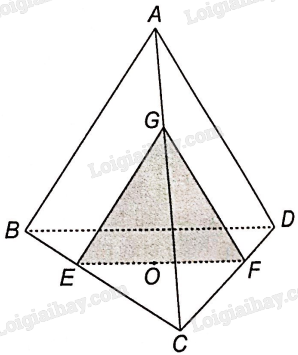
a) Qua O kẻ đường thẳng song song với BD cắt BC tại E, cắt CD tại F. Khi đó, EF là giao tuyến của mặt phẳng (P) và mặt phẳng (BCD).
b) Trong mặt phẳng (ABC), vẽ EG//AB (G thuộc AC) thì EG là giao tuyến của mặt phẳng (P) với mặt phẳng ABC.
Ta có: G thuộc AC nằm trong mặt phẳng ACD, F thuộc DC nằm trong mặt phẳng ACD. Khi đó, GF là giao tuyến của mặt phẳng (P) và mặt phẳng (ACD).
Bài 4.31 trang 67 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E là một điểm bất kì thuộc cạnh SA và (P) là mặt phẳng qua E song song với mặt phẳng (ABCD).
a) Xác định giao tuyến của mặt phẳng (P) và các mặt bên của hình chóp.
b) Hình tạo bởi các giao tuyến là hình gì? Giải thích vì sao.
Lời giải:
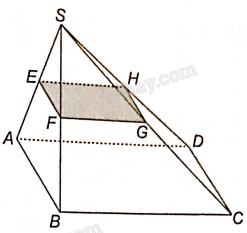
a) Trong mặt phẳng (SAB), qua E kẻ đường thẳng song song với AB cắt SB tại F. Khi đó, EF là giao tuyến của mặt phẳng (P) và mặt phẳng (SAB).
Trong mặt phẳng (SBC), qua F kẻ đường thẳng song song với BC cắt SC tại G. Khi đó, FG là giao tuyến của mặt phẳng (P) và mặt phẳng (SBC).
Trong mặt phẳng (SCD), qua G kẻ đường thẳng song song với DC cắt SD tại H. Khi đó, GH là giao tuyến của mặt phẳng (P) và mặt phẳng (SCD).
Vì E vừa thuộc mặt phẳng (P) vừa thuộc mặt phẳng (SAD); H vừa thuộc mặt phẳng (P) vừa thuộc mặt phẳng (SAD) nên EH là giao tuyến của (P) và mặt phẳng (SAD)
b) Vì mp (ABCD)//mp (EFGH), EH là giao tuyến của mp (EFGH) và mp (SAD), AD là giao tuyến của mp (ABCD) và mp (SAD) nên EH//AB.
Vì EH//AD, AD//BC nên EH//BC
Mà FG//BC nên EH//FG
Vì EF//AB, AB//CD nên EF//DC
Mà HG//DC nên EF//HG
Tứ giác EFGH có: EF//GH, EH//FG nên tứ giác EFGH là hình bình hành.
Bài 4.32 trang 67 SBT Toán 11 Tập 1: Cho hình lăng trụ tứ giác ABCD.A’B’C’D’ có đáy ABCD là hình thang. Chứng minh rằng đáy A’B’C’D’ là hình thang.
Lời giải:
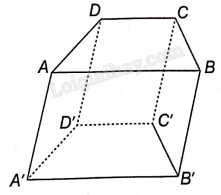
Giả sử AB//CD
Các mặt ABB’A’ và CDD’C’ của hình lăng trụ là hình bình hành nên AB//A’B’, CD//C’D’
Do đó, A’B’//C’D’
Suy ra, đáy A’B’C’D’ là hình thang.
Bài 4.33 trang 68 SBT Toán 11 Tập 1: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Chứng minh rằng sau điểm A, B, C, D, E, F là sáu đỉnh của một hình lăng trụ tam giác.
Lời giải:
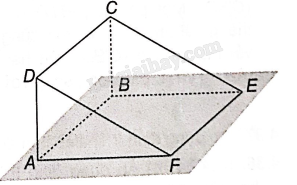
Vì AD//BC (do ABCD là hình bình hành) nên AD//mp (BCE), AF//BE (do ABEF là hình bình hành) nên AF//mp (BCE).
Mà AD và AF là hai đường thẳng cắt nhau cùng nằm trong mặt phẳng ADF. Do đó, mp (ADF) //mp (BCE).
Các đường thẳng AB, CD, EF đôi một song song với nhau.
Bài 4.34 trang 68 SBT Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Một mặt phẳng (P) cắt các cạnh AD, BC, B’C’, A’D’ lần lượt tại E, F, G, H. Chứng minh rằng tứ giác EFGH là hình bình hành.
Lời giải:
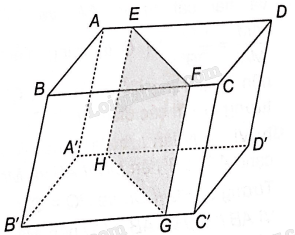
Vì hai mặt phẳng (ABCD) và (A’B’C’D’) của hình hộp song song với nhau nên giao tuyến của mặt phẳng (EFGH) và hai mặt phẳng đó song song với nhau, tức là EF//GH
Vì hai mặt phẳng (AA’D’D) và (B’B’C’B) của hình hộp song song với nhau nên giao tuyến của mặt phẳng (EFGH) và hai mặt phẳng đó song song với nhau, tức là EH//GF
Tứ giác EFGH có: EF//GH, EH//GF nên tứ giác EFGH là hình bình hành.
Bài 4.35 trang 68 SBT Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’.
a) Xác định giao tuyến d của hai mặt phẳng (ADC’B’) và (A’D’CB).
b) Chứng minh rằng d // AD.
c) Chứng minh rằng d đi qua trung điểm của các đường chéo của hình hộp.
Lời giải:
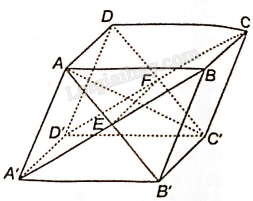
a) Gọi E là giao điểm của AB’ và A’B; gọi F là giao điểm của CD’ và C’D. Vì đường thẳng EF vừa thuộc cả hai mặt phẳng (ADC’B’) và (A’D’CB) nên EF là giao tuyến của hai mặt phẳng (ADC’B’) và (A’D’CB).
b) Hai mặt phẳng (ADC’B’) và (A’D’CB) chứa hai đường thẳng song song là AD và BC nên giao tuyến EF của hai mặt phẳng đó song song với AD.
c) Tứ giác ABCD và BCC’B’ là hình bình hành nên AD//BC, và BC//B’C’ và , do đó ADC’B’ là hình bình hành.
Vì E, F lần lượt là trung điểm của AB’ và CD’ nên EF đi qua trung điểm của AC’. Vì các đường chéo của hình hộp cùng đi qua trung điểm của mỗi đường nên đường thẳng EF đi qua trung điểm các đường chéo đó.
Bài 4.36 trang 68 SBT Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng:
a) AB’//C’D’;
b) Hai mặt phẳng (AB’D’) và (C’B’D) song song với nhau.
Lời giải:
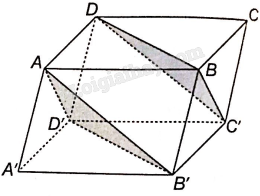
a) Tứ giác ABCD và BCC’B’ là hình bình hành nên AD//BC, và BC//B’C’ và , do đó ADC’B’ là hình bình hành nên AB’//C’D.
b) Vì AB’//C’D nên AB’//mp(C’BD)
Chứng minh tương tự ta có: AD’//BC’ nên AD’//mp(C’BD). Mặt phẳng (AB’D’) có hai đường thẳng cắt nhau AB’ và AD’ cùng song song với mp(C’BD) nên hai mặt phẳng (AB’D’) và (C’B’D) song song với nhau.
Bài 4.37 trang 68 SBT Toán 11 Tập 1: Cho ba mặt phẳng (P), (Q), (R) đôi một song song. Hai đường thẳng d, d’ cắt ba mặt phẳng lần lượt tại A, B, C và A’, B’, C’. Biết rằng AB = 2cm, BC = 6cm và A’B’ = 3cm, tính B’C’.
Lời giải:
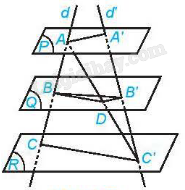
Vì ba mặt phẳng (P), (Q), (R) đôi một song song và hai đường thẳng d, d’ cắt ba mặt phẳng lần lượt tại A, B, C và A’, B’, C’ nên (định lí Thalès)
Bài 4.38 trang 68 SBT Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Gọi O là giao điểm của các đường chéo của hình hộp. Mặt phẳng qua O và song song với mặt phẳng (ABCD) cắt các cạnh AA’, BB’, CC’, DD’ lần lượt tại M, N, P, Q.
a) Chứng minh rằng M, N, P, Q lần lượt là trung điểm của các cạnh AA’, BB’, CC’, DD’.
b) Chứng minh rằng ABCD.MNPQ là hình hộp.
Lời giải:
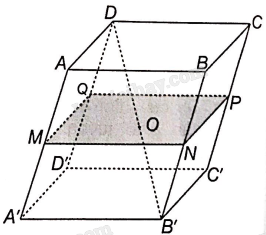
a) Áp dụng định lí Thalès cho ba mặt phẳng (ABCD), (MNPQ), (A’B’C’D’) và hai cát tuyến AA’, DB’ ta có:
Vì O là trung điểm của DB’ nên M là trung điểm của AA’.
Chứng minh tương tự ta có: N, P, Q lần lượt là trung điểm của BB’, CC’, DD’.
b) Vì M, N lần lượt là trung điểm của AA’, BB’ nên MN//AB,
Tương tự ta có: PQ//CD và
Vì và AB//CD nên và MN//PQ.
Do đó tứ giác MNPQ là hình bình hành.
Vì các đường thẳng AM, BN, CP, DQ đôi một song song nên suy ra ABCD.MNPQ là hình hộp.
Bài 4.39 trang 68 SBT Toán 11 Tập 1: Khi cắt một chiếc bánh gato hình hộp, Thúy nhận thấy vết cắt ở mặt trên và mặt dưới của bánh gợi nên hình ảnh về hai đường thẳng song song với nhau. Hỏi nhận xét của Thúy có đúng không? Vì sao?
Lời giải:
Khi Thúy cắt bánh thì lưỡi dao di chuyển tạo thành một mặt phẳng cắt hai mặt trên và dưới của chiếc bánh. Vì mặt trên và mặt dưới của chiếc bánh song song với nhau nên các vết cắt (chính là giao tuyến của mặt phẳng cắt và hai mặt bánh) song song với nhau.
Bài 4.40 trang 68 SBT Toán 11 Tập 1: Một chiếc bình nước hình trụ được đặt trên bàn, lượng nước trong bình bằng đúng một nửa dung tích của bình. Hoàng đặt một chiếc ống hút vào trong bình sao cho cho một đầu của ống hút chạm vào đáy bình còn một đầu chạm vào miệng bình. Hoàng nói rằng độ dài của phần ống hút bị ướt bằng độ dài của toàn bộ ống hút. Hỏi Hoàng nói đúng hay sai? Vì sao?
Lời giải:
Hoàng nói sai, theo định lí Thalès trong không gian thì độ dài của phần ống bị ướt bằng độ dài của toàn bộ ống hút.
Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 12: Đường thẳng và mặt phẳng song song
Bài 13: Hai mặt phẳng song song
Bài 14: Phép chiếu song song
Bài tập cuối chương 4
Bài 15: Giới hạn của dãy số