Bài 9: Các số đặc trưng đo xu thế trung tâm

Giải SBT Toán 11 Bài 9: Các số đặc trưng đo xu thế trung tâm

Bài 3.5 trang 50 SBT Toán 11: Quãng đường (km) các cầu thủ (không tính thủ môn) chạy trong một trận đấu bóng đá tại giải ngoại hạng Anh được cho trong bảng thống sau:

Tính quãng đường trung bình một cầu thủ chạy trong trận đấu này.

Lời giải: 

Quãng đường trung bình cầu thủ chạy trong trận đấu là:

$\frac{3,2 + 5,5 + 7,6 + 9,9 + 11,3}{2+5+6+9+3}=7,48\left(km\right)$

Bài 3.6 trang 50 SBT Toán 11: Quãng đường (km) các cầu thủ (không tính thủ môn) chạy trong một trận đấu bóng đá tại giải ngoại hạng Anh được cho trong bảng thống sau:

Tìm trung vị của mẫu số liệu này và giải thích ý nghĩa của giá trị thu được.

Lời giải:

Cỡ mẫu n = 2 + 5 + 6 + 9 + 3 = 25. Nhóm chứa trung vị là [6;80). Trung vị là:

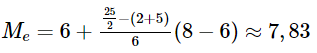
Có 50% số cầu thủ chạy nhiều hơn 7,83km và có 50% số cầu thủ chạy ít hơn 7,83km.

Bài 3.7 trang 50 SBT Toán 11: Quãng đường (km) các cầu thủ (không tính thủ môn) chạy trong một trận đấu bóng đá tại giải ngoại hạng Anh được cho trong bảng thống sau:

Tìm a sao cho có 25% số cầu thủ tham gia trận đấu chạy ít nhất a(km).

Lời giải:

Số a chính là tứ phân vị thứ ba.

Tứ phân vị thứ ba a là $\frac{x_{18}+x_{19}}{2}$. Do x₁₈; x₁₉ đều thuộc nhóm [8;10) nên nhóm này chứa a. Do đó, p = 4; a₄ = 8; m₄ = 9; m₁ + m₂ + m₃ = 2+5+6 = 13; a₅ – a₄ = 2

Suy ra: $a=8 +\frac{\frac{3,25}{4}–13}{9}.2=\frac{167}{18}$

Bài 3.8 trang 50 SBT Toán 11: Quãng đường (km) các cầu thủ (không tính thủ môn) chạy trong một trận đấu bóng đá tại giải ngoại hạng Anh được cho trong bảng thống sau:

Tính mốt của mẫu số liệu và giải thích ý nghĩa của giá trị thu được

Lời giải:

Nhóm chứa mốt là [8; 10). Mốt là: 

Số cầu thủ chạy khoảng 8,67km là nhiều nhất.

Bài 3.9 trang 50 SBT Toán 11: Thống kê số lần đi học muộn trong học kì của các bạn trong lớp, Nam thu được kết quả sau:

Trung bình mỗi học sinh trong lớp đi muộn bao nhiêu buổi trong học kì?

Lời giải:

Ta có bảng số liệu ghép nhóm:

Trung bình mỗi học sinh trong học kì đi muộn số buổi là:

Bài 3.10 trang 50 SBT Toán 11: Thống kê số lần đi học muộn trong học kì của các bạn trong lớp, Nam thu được kết quả sau:

Tính các tứ phân vị của mẫu số liệu ghép nhóm và cho biết ý nghĩa của các kết quả thu được.

Lời giải:

Ta có bảng số liệu ghép nhóm:

Cỡ mẫu $n=40$

+ Tứ phân vị thứ nhất $Q_1$ là $\frac{x_{10}+x_{11}}{2}$. Do $x_{10},x_{11}$ đều thuộc nhóm $\left[0;3\right)$ nên nhóm này chứa $Q_1$. Do đó, $p=1,a_1=0,m_1=23,a_2-a_1=3$

Suy ra: $Q_1=0+\frac{\frac{40}{4}-0}{23}.3=\frac{30}{23}$

+ Tứ phân vị thứ ba $Q_3$ là $\frac{x_{30}+x_{31}}{2}$. Do $x_{30},x_{31}$ đều thuộc nhóm $\left[3;6\right)$ nên nhóm này chứa $Q_3$. Do đó, $p=2,a_2=3,m_2=8,m_1=233,a_3-a_2=3$

Suy ra: $Q_3=3+\frac{\frac{3.40}{4}-23}{8}.3=5,625$.

+ Tứ phân vị $Q_2$ chính là trung vị $M_e$

Nhóm chứa trung vị là $\left[0;3\right)$. Trung vị là: $M_e=0+\frac{\frac{40}{2}-0}{23}\left(3-0\right)=\frac{60}{23}$

Vậy $Q_2=\frac{60}{23}$.

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 8: Mẫu số liệu ghép nhóm

Bài 9: Các số đặc trưng đo xu thế trung tâm

Bài tập cuối chương 3

Bài 10: Đường thẳng và mặt phẳng trong không gian

Bài 11: Hai đường thẳng song song