Giải SGK Toán 7 Bài 6 (Cánh diều): Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh

Giải bài tập Toán lớp 7 Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

A. Câu hỏi trong bài

Giải Toán 7 trang 88 Tập 2

Câu hỏi khởi động trang 88 Toán 7 Tập 2: Có ba trạm quan sát A, B, C trong đó trạm quan sát C ở giữa hồ.

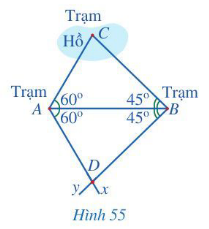
Giải Toán 7 Bài 6 (Cánh diều): Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (ảnh 1)

Người ta muốn đo khoảng cách từ A và từ B đến C. Do không thể đo trực tiếp được các khoảng cách trên nên người ta làm như sau (Hình 55):

– Đo góc BAC được 60°, đo góc ABC được 45°;

– Kẻ tia Ax sao cho $\hat{B A x} = 60 °$ , kẻ tia By sao cho $\hat{A B y} = 45 °$ , xác định giao điểm D của hai tia đó;

– Đo khoảng cách AD và BD. Ta có AC = AD và BC = BD.

Tại sao lại có hai đẳng thức trên?

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Bài toán được mô tả bởi hai tam giác ABC và tam giác ABD như Hình 55.

$∆$ ABC, $∆$ ABD,

$\hat{B A C} = \hat{D A B} = 60 °,$

$\hat{A B C} = \hat{A B D} = 45 °$

AC = AD và BC = BD.

Chứng minh (Hình 55):

Xét $∆$ ABC và $∆$ ABD có:

$\hat{B A C} = \hat{D A B} (= 60 °)$ (giả thiết),

AB chung,

$\hat{A B C} = \hat{A B D} (= 45 °)$ (giả thiết)

Suy ra $∆$ ABC = $∆$ ABD (g.c.g)

Do đó AC = AD và BC = BD (các cặp cạnh tương ứng).

Vậy AC = AD và BC = BD.

Hoạt động 1 trang 88 Toán 7 Tập 2: Cho tam giác ABC (Hình 56).

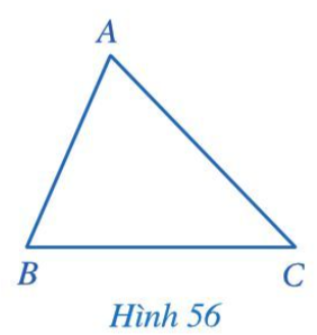
Giải Toán 7 Bài 6 (Cánh diều): Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (ảnh 1)

Những góc nào của tam giác ABC có cạnh thuộc đường thẳng AB?

Trong tam giác ABC (Hình 56), ta gọi góc A và góc B là hai góc kề cạnh AB. Tương tự, góc B và góc C là hai góc kề cạnh BC, góc C và góc A là hai góc kề cạnh CA.

Lời giải:

Ta có $\hat{B A C}$ gồm hai cạnh lần lượt thuộc hai đường thẳng AB và AC;

$\hat{A B C}$ gồm hai cạnh lần lượt thuộc hai đường thẳng AB và BC.

Vậy, những góc của tam giác ABC có cạnh thuộc đường thẳng AB là: $\hat{B A C}$ và $\hat{A B C}$

Hoạt động 2 trang 88 Toán 7 Tập 2: Cho hai tam giác ABC và A’B’C’ (Hình 57) có: $\hat{A} = \hat{A^{‘}} = 60 °,$ AB = A’B’ = 3 cm, $\hat{B} = \hat{B^{‘}} = 45 °$ .

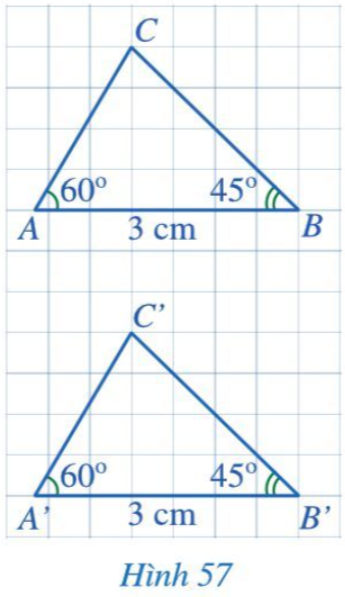
Giải Toán 7 Bài 6 (Cánh diều): Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (ảnh 1)

Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?

Lời giải:

Dựa vào hình trên, bằng cách đếm số ô vuông, ta thấy:

+) Cạnh BC là đường chéo của hình vuông có độ dài cạnh bằng 4 độ dài cạnh ô vuông;

+) Cạnh B’C’ là đường chéo của hình vuông có độ dài cạnh bằng 4 độ dài cạnh ô vuông;

Do đó BC = B’C’.

Xét $∆$ ABC và $∆$ A’B’C’ có:

AB = A’B’ (= 3cm).

$\hat{A B C} = \hat{A^{‘} B^{‘} C^{‘}} (= 45 °)$ .

BC = B’C’ (chứng minh trên).

Suy ra $∆$ ABC = $∆$ A’B’C’ (c.g.c)

Vậy $∆$ ABC = $∆$ A’B’C’.

Giải Toán 7 trang 89 Tập 2

Luyện tập 1 trang 89 Toán 7 Tập 2: Cho hai tam giác ABC và A’B’C’ thỏa mãn: BC = B’C’ = 3 cm, $\hat{B} = \hat{B^{‘}} = 60 °$ , $\hat{C} = 50 °$ , $\hat{A^{‘}} = 70 °$ . Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?

Lời giải:

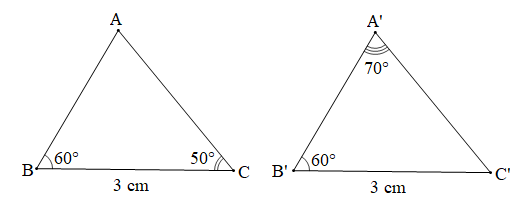
Giải Toán 7 Bài 6 (Cánh diều): Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (ảnh 1)

Xét tam giác A’B’C’ có: $\hat{A^{‘}} + \hat{B^{‘}} + \hat{C^{‘}} = 180 °$ (tổng ba góc trong một tam giác)

Suy ra: $\hat{C^{‘}} = 180 ° - \hat{A^{‘}} - \hat{B^{‘}} = 180 ° - 70 ° - 60 ° = 50 °$ .

Xét $∆$ ABC và $∆$ A’B’C’ có:

$\hat{B} = \hat{B^{‘}} (= 60 °)$ .

BC = B’C’ (theo giả thiết).

$\hat{C} = \hat{C^{‘}} (= 50 °)$ .

Suy ra $∆$ ABC = $∆$ A’B’C’ (g.c.g)

Vậy $∆$ ABC = $∆$ A’B’C’.

Luyện tập 2 trang 89 Toán 7 Tập 2: Giải thích bài toán ở phần mở đầu.

Lời giải:

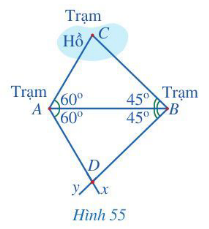
Giải Toán 7 Bài 6 (Cánh diều): Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (ảnh 1)

Bài toán được mô tả bởi hai tam giác ABC và tam giác ABD như Hình 55.

$∆$ ABC, $∆$ ABD,

$\hat{B A C} = \hat{D A B} = 60 °,$

$\hat{A B C} = \hat{A B D} = 45 °$

AC = AD và BC = BD.

Chứng minh (Hình 55):

Xét $∆$ ABC và $∆$ ABD có:

$\hat{B A C} = \hat{D A B} (= 60 °)$ (giả thiết),

AB chung,

$\hat{A B C} = \hat{A B D} (= 45 °)$ (giả thiết)

Suy ra $∆$ ABC = $∆$ ABD (g.c.g)

Do đó AC = AD và BC = BD (các cặp cạnh tương ứng).

Vậy AC = AD và BC = BD.

B. Bài tập

Giải Toán 7 trang 91 Tập 2

Bài 1 trang 91 Toán 7 Tập 2: Cho hai tam giác ABC và A’B’C’ thỏa mãn: AB = A’B’, $\hat{A} = \hat{A^{‘}}$ , $\hat{C} = \hat{C^{‘}}$ . Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?

Lời giải:

Giải Toán 7 Bài 6 (Cánh diều): Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (ảnh 1)

$∆$ ABC, $∆$ A’B’C’,

AB = A’B’, $\hat{A} = \hat{A^{‘}}, \hat{C} = \hat{C^{‘}}$

$∆$ ABC và $∆$ A’B’C’ có bằng nhau không? Vì sao?

Xét tam giác ABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$ (tổng ba góc trong một tam giác)

Suy ra: $\hat{B} = 180 ° - \hat{A} - \hat{C}$ .

Xét tam giác A’B’C’ có: $\hat{A^{‘}} + \hat{B^{‘}} + \hat{C^{‘}} = 180 °$ (tổng ba góc trong một tam giác)

Suy ra: $\hat{B^{‘}} = 180 ° - \hat{A^{‘}} - \hat{C^{‘}}$ .

Mà $\hat{A} = \hat{A^{‘}}$ , $\hat{C} = \hat{C^{‘}}$ (giả thiết) nên $\hat{ B} = \hat{B^{‘}}$ .

Xét $∆$ ABC và $∆$ A’B’C’ có:

$\hat{A} = \hat{A^{‘}}$ (giả thiết),

AB = A’B’ (giả thiết),

$\hat{ B} = \hat{B^{‘}}$ (giả thiết).

Suy ra $∆$ ABC = $∆$ A’B’C’ (g.c.g).

Vậy $∆$ ABC = $∆$ A’B’C’.

Bài 2 trang 91 Toán 7 Tập 2: Cho Hình 65 có AM = BN, $\hat{A} = \hat{B}$ .

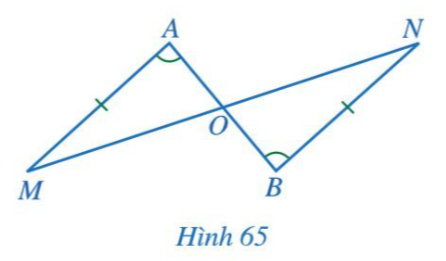
Giải Toán 7 Bài 6 (Cánh diều): Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (ảnh 1)

Chứng minh: OA = OB, OM = ON.

Lời giải:

$∆$ AMO, $∆$ BNO,

AM = BN, $\hat{A} = \hat{B}$ .

OA = OB, OM = ON.

Chứng minh (Hình 65):

Xét $∆$ AMO có: $\hat{A M O} + \hat{A} + \hat{A O M} = 180 °$ (tổng ba góc trong một tam giác)

Suy ra: $\hat{A M O} = 180 ° - \hat{A} - \hat{A O M}$ . (1)

Xét $∆$ BNO có: $\hat{B N O} + \hat{B} + \hat{B O N} = 180 °$ (tổng ba góc trong một tam giác)

Suy ra: $\hat{B N O} = 180 ° - \hat{B} - \hat{B O N}$ . (2)

Mà $\hat{A} = \hat{B}$ (theo giả thiết), $\hat{A O M} = \hat{B O N}$ (hai góc đối đỉnh) (3)

Từ (1), (2) và (3) ta có: $\hat{A M O} = \hat{B N O}$ .

Xét $∆$ AMO và $∆$ BNO có:

$\hat{A} = \hat{B}$ (giả thiết).

AM = BN (giả thiết).

$\hat{A M O} = \hat{B N O}$ (chứng minh trên).

Suy ra $∆$ AMO và $∆$ BNO (g.c.g).

Do đó OA = OB và OM = ON (các cặp cạnh tương ứng).

Giải Toán 7 trang 92 Tập 2

Bài 3 trang 92 Toán 7 Tập 2: Cho Hình 66 có $\hat{N} = \hat{P} = 90 °, \hat{P M Q} = \hat{N Q M} .$ Chứng minh MN = QP, MP = QN.

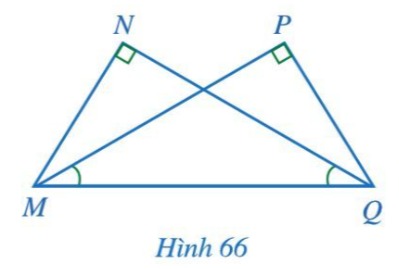
Giải Toán 7 Bài 6 (Cánh diều): Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (ảnh 1)

Lời giải:

$∆$ MNQ, $∆$ MPQ,

$\hat{N} = \hat{P} = 90 °, \hat{P M Q} = \hat{N Q M} .$

MN = QP, MP = QN.

Chứng minh (Hình 66):

Tam giác MNQ có $\hat{N} = 90 °$ (giả thiết) nên tam giác MNQ vuông tại N.

Tam giác QPM có $\hat{P} = 90 °$ (giả thiết) nên tam giác MPQ vuông tại P.

Xét $∆$ MNQ (vuông tại N) và $∆$ MPQ (vuông tại P) có:

$\hat{N Q M} = \hat{P M Q}$ (giả thiết).

MQ chung.

Suy ra $∆$ MNQ = $∆$ QPM (cạnh huyền – góc nhọn).

Do đó MN = QP và MP = QN (các cặp cạnh tương ứng).

Vậy MN = QP và MP = QN.

Bài 4 trang 92 Toán 7 Tập 2: Cho Hình 67 có $\hat{A H D} = \hat{B K C} = 90 °,$ DH = CK, $\hat{D A B} = \hat{C B A} .$ Chứng minh AD = BC.

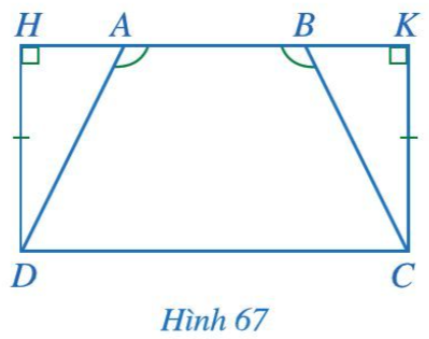
Giải Toán 7 Bài 6 (Cánh diều): Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (ảnh 1)

Lời giải:

$∆$ AHD, $∆$ BKC,

$\hat{A H D} = \hat{B K C} = 90 °,$

DH = CK, $\hat{D A B} = \hat{C B A} .$

AD = BC.

Chứng minh (Hình 67):

Xét tam giác AHD có: $\hat{D A B}$ là góc ngoài tại đỉnh A của tam giác nên $\hat{D A B} = \hat{A H D} + \hat{A D H}$ (tính chất góc ngoài của tam giác)

Hay $\hat{D A B} = 90 ° + \hat{A D H}$ .

Xét tam giác BKC có: $\hat{C B A}$ là góc ngoài tại đỉnh B của tam giác nên $\hat{C B A} = \hat{B K C} + \hat{B C K}$ (tính chất góc ngoài của tam giác)

Hay $\hat{C B A} = 90 ° + \hat{B C K}$ .

Mà $\hat{D A B} = \hat{C B A}$ (giả thiết) nên $\hat{A D H} = \hat{B C K}$ .

Tam giác AHD có $\hat{A H D} = 90 °$ nên là tam giác vuông tại H.

Tam giác BKC có $\hat{B K C} = 90 °$ nên là tam giác vuông tại K.

Xét $∆$ AHD (vuông tại H) và $∆$ BKC (vuông tại K) có:

DH = CK (giả thiết),

$\hat{A D H} = \hat{B C K}$ (chứng minh trên).

Suy ra $∆$ AHD = $∆$ BKC (cạnh góc vuông – góc nhọn kề)

Do đó AD = BC (hai cạnh tương ứng).

Vậy AD = BC.

Bài 5 trang 92 Toán 7 Tập 2: Cho tam giác ABC có $\hat{B} > \hat{C} .$ Tia phân giác góc BAC cắt cạnh BC tại điểm D.

a) Chứng minh $\hat{A D B} < \hat{A D C}$ .

b) Kẻ tia Dx nằm trong góc ADC sao cho $\hat{A Dx} = \hat{A D B}$ . Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh: $∆$ ABD = $∆$ AED, AB < AC.

Lời giải:

$∆$ ABC, $\hat{B} > \hat{C} .$

AD là tia phân giác của $\hat{B A C}$

b) Tia Dx nằm trong $\hat{A D C}$ , $\hat{A DE} = \hat{A D B}$ (E là giao điểm của Dx và AC)

a) $\hat{A D B} < \hat{A D C}$ .

b) $∆$ ABD = $∆$ AED, AB < AC.

Chứng minh (Hình vẽ dưới đây):

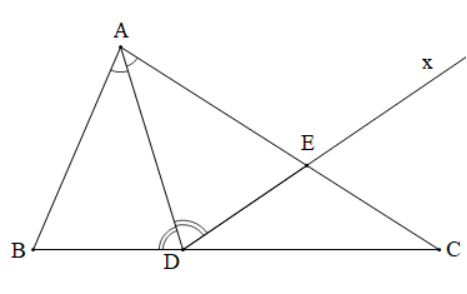
Giải Toán 7 Bài 6 (Cánh diều): Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (ảnh 1)

a) Xét tam giác ABD có: $\hat{A DC}$ là góc ngoài tại đỉnh D của tam giác nên $\hat{A D C} = \hat{B A D} + \hat{B}$ .

Xét tam giác ABD có: $\hat{A D C}$ là góc ngoài tại đỉnh D của tam giác nên $\hat{A D B} = \hat{C A D} + \hat{C}$ .

Mà AD là tia phân giác của $\hat{B A C}$ (giả thiết) nên $\hat{B A D} = \hat{C A D}$ (tính chất tia phân giác của một góc)

Lại có $\hat{B} > \hat{C}$ (giả thiết) nên $\hat{B A D} + \hat{B} > \hat{C A D} + \hat{C}$ hay $\hat{A D C} > \hat{A D B}$ .

Vậy $\hat{A D B} < \hat{A D C}$

b) Xét $∆$ ABD và $∆$ AED có:

$\hat{B A D} = \hat{E A D}$ (chứng minh trên),

AD chung,

$\hat{A D B} = \hat{A D E}$ (giả thiết).

Suy ra $∆$ ABD = $∆$ AED (g.c.g).

Vậy $∆$ ABD = $∆$ AED.

* Chứng minh AB < AC:

Cách 1:

Vì $∆$ ABD = $∆$ AED (chứng minh trên) nên AB = AE (hai cạnh tương ứng)

Mà AE < AC (do điểm E nằm trên cạnh AC)

Nên AB < AC.

Vậy AB < AC.

Cách 2: Xét tam giác ABC có $\hat{B} > \hat{C}$ (giả thiết)

Mà cạnh AB đối diện với góc C, cạnh AC đối diện với góc C

Do đó AC > AB.

Vậy AB < AC.

Bài 6 trang 92 Toán 7 Tập 2: Cho $∆$ ABC = $∆$ MNP. Tia phân giác của góc BAC và NMP lần lượt cắt các cạnh BC và NP tại D, Q. Chứng minh AD = MQ.

Lời giải:

$∆$ ABC = $∆$ MNP,

AD là tia phân giác của $\hat{B A C},$

MQ là tia phân giác của $\hat{N M P},$

AD = MQ.

Chứng minh (Hình vẽ dưới đây):

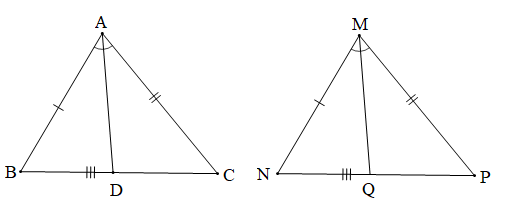
Giải Toán 7 Bài 6 (Cánh diều): Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (ảnh 1)

Vì $∆$ ABC = $∆$ MNP (giả thiết) nên:

+) $\hat{B A C} = \hat{N M P}$ và $\hat{B} = \hat{N}$ (các cặp góc tương ứng);

+) AB = MN (hai cạnh tương ứng).

Ta có:

+) AD là tia phân giác của $\hat{B A C}$ (giả thiết) nên $\hat{B A D} = \frac{1}{2} \hat{B A C}$ (tính chất tia phân giác của một góc)

+) MQ là tia phân giác của $\hat{N M P}$ (giả thiết) nên $\hat{N M Q} = \frac{1}{2} \hat{N M P}$ (tính chất tia phân giác của một góc)

Mà $\hat{B A C} = \hat{N M P}$ (chứng minh trên) nên $\hat{B A D} = \hat{N M Q}$ .

Xét $∆$ ABD và $∆$ MNQ có:

$\hat{B A D} = \hat{N M Q}$ (chứng minh trên),

AB = MN (chứng minh trên),

$\hat{B} = \hat{N}$ (chứng minh trên).

Suy ra $∆$ ABD = $∆$ MNQ (g.c.g).

Do đó AD = MQ (hai cạnh tương ứng).

Vậy AD = MQ.

====== ****&**** =====

Bài liên quan:

Leave a Comment Hủy