Lý thuyết Toán lớp 10 Bài 2: Giải tam giác. Tính diện tích tam giác

Với tóm tắt lý thuyết Toán lớp 10 Bài 2: Giải tam giác. Tính diện tích tam giác sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 10.
Lý thuyết Toán lớp 10 Bài 2: Giải tam giác. Tính diện tích tam giác

Video giải Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác – Cánh diều
A. Lý thuyết Giải tam giác. Tính diện tích tam giác
1. Giải tam giác
Như ta đã biết, một tam giác hoàn toàn xác định nếu biết một trong những dữ kiện sau:
– Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó;
– Biết độ dài ba cạnh;
– Biết độ dài một cạnh và độ lớn hai góc kề với cạnh đó.
Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.
Ví dụ: Cho tam giác ABC có AB = 4, BC = 6, AC = $2\sqrt{7}$. Điểm M thuộc đoạn BC sao cho MC = 2MB.
a) Tính cos các góc của tam giác ABC.
b) Tính độ dài cạnh AM.
Hướng dẫn giải:

a) Theo định lí cosin trong tam giác ABC ta có:
cosB = $\frac{{\mathrm{AB}}^2+{\mathrm{BC}}^2-{\mathrm{AC}}^2}{2\mathrm{AB}.\mathrm{BC}}$= $\frac{4^2+6^2-{\left(2\sqrt{7}\right)}^2}{\mathrm{2.4.6}}$= $\frac{1}{2}$
⇒ $\widehat{\mathrm{B}}$= 60°.
cosC = $\frac{{\mathrm{AC}}^2+{\mathrm{BC}}^2-{\mathrm{AB}}^2}{2\mathrm{AC}.\mathrm{BC}}$= $\frac{{\left(2\sqrt{7}\right)}^2+6^2-4^2}{2.2\sqrt{7}.6}$= $\frac{2\sqrt{7}}{7}$
cosA = $\frac{{\mathrm{AB}}^2+{\mathrm{AC}}^2-{\mathrm{BC}}^2}{2\mathrm{AB}.\mathrm{AC}}$= $\frac{4^2+{\left(2\sqrt{7}\right)}^2-6^2}{\mathrm{2.4.2}\sqrt{7}}$= $\frac{\sqrt{7}}{14}$
b) Ta có:
MC = 2MB ⇒ $\frac{\mathrm{MB}}{\mathrm{MC}}$= $\frac{1}{2}$⇒ $\frac{\mathrm{MB}}{\mathrm{BC}}$= $\frac{1}{3}$
⇒ MB = $\frac{1}{3}$BC = $\frac{1}{3}$.6 = 2
Áp dụng định lí côsin trong tam giác AMB ta có:
AM² = AB² + BM² – 2AB.BM.cosB = 4² + 2² – 2.4.2. $\frac{1}{2}$= 12
⇒ AM = $\sqrt{12}$= $2\sqrt{3}$
Ví dụ: Cho tam giác ABC có $\widehat{\mathrm{B}}=35°$; $\widehat{\mathrm{C}}=50°$ và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC (làm tròn đến chữ số thập phân thứ 2).
Hướng dẫn giải:

Ta có:
$\widehat{\mathrm{A}}$ + $\widehat{\mathrm{B}}$ + $\widehat{\mathrm{C}}$= 180° (tổng ba góc trong tam giác)
Suy ra:
$\widehat{\mathrm{A}}$ = 180° – $\widehat{\mathrm{B}}$ – $\widehat{\mathrm{C}}$ = 180° – 35° – 50° = 95°
Áp dụng định lí sin trong tam giác ABC ta có:
$\frac{\mathrm{BC}}{\mathrm{sinA}}$ = $\frac{\mathrm{AC}}{\mathrm{sinB}}$ = $\frac{\mathrm{AB}}{\mathrm{sinC}}$
Suy ra:
BC = $\frac{\mathrm{AC}.\mathrm{sinA}}{\mathrm{sinB}}$= $\frac{15.\sin 95°}{\sin 35°}$≈ 26,05cm
AB = $\frac{\mathrm{AC}.\mathrm{sinC}}{\mathrm{sinB}}$= $\frac{15.\sin 50°}{\sin 35°}$≈ 20,03cm
Vậy BC = 26,05cm và AB ≈ 20,03 cm.
2. Tính diện tích tam giác
Công thức tính diện tích tam giác:
• Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó, diện tích S của tam giác ABC là:
S = $\frac{1}{2}$bc.sinA = $\frac{1}{2}$ca.sin = $\frac{1}{2}$ab.sinC
Ví dụ: Cho tam giác ABC có BC = $4\sqrt{2}$, $\widehat{\mathrm{A}}$= 45°, $\widehat{\mathrm{B}}$= 120°. Tính diện tích tam giác ABC.
Hướng dẫn giải:
Ta có:
$\widehat{\mathrm{A}}$ + $\widehat{\mathrm{B}}$ + $\widehat{\mathrm{C}}$= 180° (tổng ba góc trong tam giác)
Suy ra: $\widehat{\mathrm{C}}$= 180° – $\widehat{\mathrm{A}}$ – $\widehat{\mathrm{B}}$ = 180° – 45° – 120° = 15°
Áp dụng định lí sin trong tam giác ABC ta có:
$\frac{\mathrm{BC}}{\mathrm{sinA}}$ = $\frac{\mathrm{AC}}{\mathrm{sinB}}$ = $\frac{\mathrm{AB}}{\mathrm{sinC}}$
Suy ra:
AC = $\frac{\mathrm{BC}.\mathrm{sinB}}{\mathrm{sinA}}$ = $\frac{4\sqrt{2}.\sin 120°}{\sin 45°}$ = $4\sqrt{3}$;
AB = $\frac{\mathrm{AC}.\mathrm{sinC}}{\mathrm{sinB}}$= $\frac{4\sqrt{3}.\sin 15°}{\sin 120°}$ = $2\sqrt{6}-2\sqrt{2}$;
Diện tích tam giác ABC là:
S = $\frac{1}{2}$AC.AB.sinA = $\frac{1}{2}.4\sqrt{3}.(2\sqrt{6}-2\sqrt{2}).\sin 45°$ = $12-4\sqrt{3}$(đơn vị diện tích).
• Công thức Heron:
Công thức toán học Heron được sử dụng để tính diện tích của một tam giác theo độ dài ba cạnh như sau:
Cho tam giác ABC có BC = a, CA = b, AB = c, $\mathrm{p}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$. Khi đó, diện tích S của tam giác ABC là:
$\mathrm{S}=\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}$.
Trong đó p là nửa chu vi tam giác ABC.
Ví dụ: Chứng minh công thức Heron.
Hướng dẫn giải:
Gọi a, b, c lần lượt là 3 cạnh của tam giác và A, B, C lần lượt là các góc đối diện của các cạnh. Theo hệ quả định lý cosin, ta có:
cosC = $\frac{{\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2}{2\mathrm{ab}}$.
Mà:
sin²C + cos²C = 1
⇒ sinC = $\sqrt{1-{\cos }^2\mathrm{C}}$= $\sqrt{1-{\left(\frac{{\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2}{2\mathrm{ab}}\right)}^2}$= $\frac{\sqrt{4{\mathrm{a}}^2{\mathrm{b}}^2-{({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2)}^2}}{2\mathrm{ab}}$
Ta có công thức tính diện tích tam giác ABC:
S = $\frac{1}{2}$absinC
   = $\frac{1}{2}$ab. $\frac{\sqrt{4{\mathrm{a}}^2{\mathrm{b}}^2-{({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2)}^2}}{2\mathrm{ab}}$
   = $\frac{1}{4}$$\sqrt{4{\mathrm{a}}^2{\mathrm{b}}^2-{({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2)}^2}$
   = $\frac{1}{4}\sqrt{(2\mathrm{ab}-({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2\left)\right)(2\mathrm{ab}+({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2\left)\right)}$
   = $\frac{1}{4}\sqrt{({\mathrm{c}}^2-{(\mathrm{a}-\mathrm{b})}^2)({(\mathrm{a}+\mathrm{b})}^2-{\mathrm{c}}^2)}$
   = $\frac{1}{4}\sqrt{(\mathrm{c}-(\mathrm{a}-\mathrm{b}\left)\right)(\mathrm{c}+(\mathrm{a}-\mathrm{b}\left)\right)\left(\right(\mathrm{a}+\mathrm{b})-\mathrm{c})\left(\right(\mathrm{a}+\mathrm{b})+\mathrm{c})}$
   = $\frac{1}{4}\sqrt{(\mathrm{a}+\mathrm{b}+\mathrm{c})(\mathrm{c}-\mathrm{a}+\mathrm{b})(\mathrm{c}+\mathrm{a}-\mathrm{b})(\mathrm{a}+\mathrm{b}-\mathrm{c})}$
   = $\frac{1}{2}(\mathrm{a}+\mathrm{b}+\mathrm{c}).\frac{1}{2}(\mathrm{a}+\mathrm{b}+\mathrm{c}-2\mathrm{a}).\frac{1}{2}(\mathrm{a}+\mathrm{b}+\mathrm{c}-2\mathrm{b}).\frac{1}{2}(\mathrm{a}+\mathrm{b}+\mathrm{c}-2\mathrm{c})$
   = $\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}$
Với $\mathrm{p}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$.
Suy ra $\mathrm{S}=\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}$ (đpcm).
Ví dụ: Cho tam giác ABC có BC = 9, CA = 6, AB = 5. Tính diện tích tam giác ABC.
Hướng dẫn giải:
Nửa chu vi tam giác ABC là:
$\mathrm{p}=\frac{\mathrm{AB}+\mathrm{AC}+\mathrm{BC}}{2}$= $\frac{5+6+9}{2}$= 10
Áp dụng công thức Heron, diện tích tam giác ABC là:
$\mathrm{S}=\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{AB})(\mathrm{p}-\mathrm{AC})(\mathrm{p}-\mathrm{BC})}$= $\sqrt{10(10-5)(10-6)(10-9)}$= $10\sqrt{2}$(đvdt)
3. Áp dụng vào bài toán thực tiễn
Trong thực tiễn, ta có thể áp dụng hệ thức lượng trong tam giác vào các bài toán như tính khoảng cách giữa hai vị trí, tính diện tích,… giúp cho việc tính toán trở nên chính xác và nhanh chóng hơn. Chúng ta có thể xem ví dụ sau:
Ví dụ: Đường dây cao thế nối thẳng từ vị trí A đến vị trí B dài 10 km, từ vị trí A đến vị trí C dài 8 km, góc tạo bởi hai đường dây trên bằng 75°. Tính khoảng cách từ vị trí B đến vị trí C (làm tròn đến chữ số thập phân thứ 2).

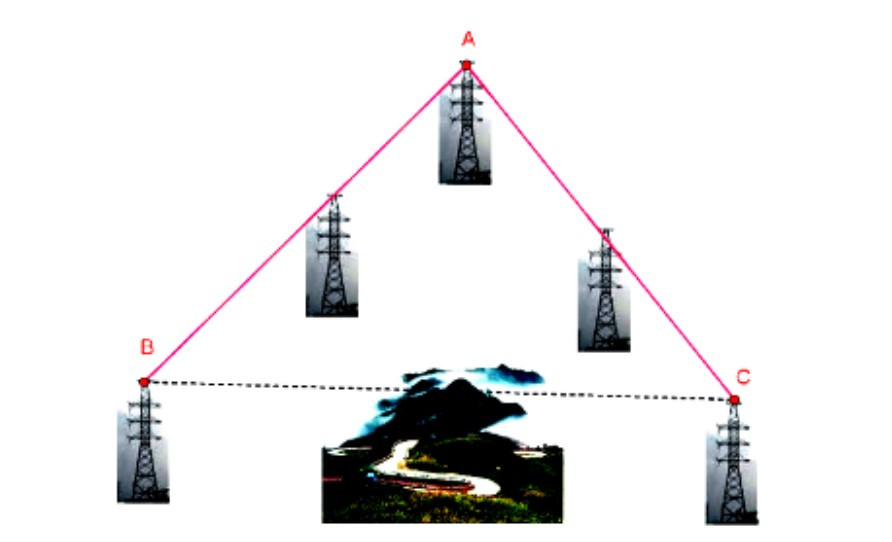
Hướng dẫn giải:
Áp dụng định lí cosin vào tam giác ABC ta có:
BC² = AB² + AC² – 2AB.AC.cosA = 8² + 10² – 2.8.10.cos75° $\approx$ 122,59
BC $\approx$ 11,07
Vậy khoảng cách từ B đến C là khoảng 11,07 km.
B. Bài tập tự luyện
B.1 Bài tập tự luận
Bài 1. Một hành khách ngồi trong máy bay, bay ở độ cao 10 km nhìn xuống hai thị trấn dưới mặt đất. Góc hợp bởi phương ngang và hai thị trấn lần lượt là 28° và 55° (hình vẽ). Tính khoảng cách giữa hai thị trấn.
Hướng dẫn giải:
Đề bài yêu cầu chúng ta tính độ dài CD.
Ta có $\widehat{\mathrm{CAD}}$= 55° – 28° = 27°.
          $\widehat{\mathrm{OAC}}$= 90° – 55° = 35°.
Và cos$\widehat{\mathrm{OAC}}$= $\frac{\mathrm{AO}}{\mathrm{AC}}$. Do đó, AC = $\frac{\mathrm{AO}}{\cos \widehat{\mathrm{OAC}}}$= $\frac{10}{\cos 35°}$≈ 12,2km.
$\widehat{\mathrm{ACO}}$= 180° – $\widehat{\mathrm{AOC}}$– $\widehat{\mathrm{OAC}}$= 180° – 90° – 35° = 55°
Trong tam giác ACD có $\widehat{\mathrm{ACD}}$= 180° – $\widehat{\mathrm{OAC}}$= 125°
Và $\widehat{\mathrm{ADC}}$= 180° – ($\widehat{\mathrm{ACD}}$+$\widehat{\mathrm{CAD}}$) = 180° – (125° + 27°) = 28°.
Áp dụng định lí sin trong tam giác ACD, ta có:
$\frac{\mathrm{CD}}{\sin 27°}=\frac{\mathrm{AC}}{\sin 28°}$⇔ CD = $\frac{12,2\sin 27°}{\sin 28°}$≈ 11,79km.
Vậy khoảng cách giữa hai thị trấn là 11,79km.
Bài 2. Một cây cột điện cao 20 m được đóng trên một triền dốc thẳng nghiêng hợp với phương nằm ngang một góc 17°. Người ta nối một dây cáp từ đỉnh cột điện đến cuối dốc. Tính chiều dài của dây cáp biết rằng đoạn đường từ đáy cọc đến cuối dốc bằng 72 m (làm tròn đến chữ số thập phân thứ 2).
Hướng dẫn giải:
                          
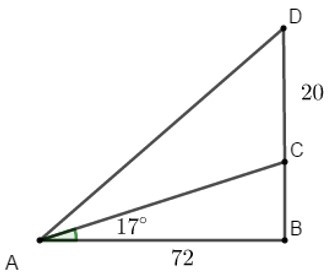
Bài toán được mô phỏng lại như hình vẽ với A, B lần lượt là điểm cuối dốc, chân của triền dốc; C, D lần lượt là chân và đỉnh của cây cột điện.
Suy ra chiều dài của dây cáp là đoạn AD.
Theo bài ra ta có: CD = 20 m, AB = 72 m, $\widehat{\mathrm{CAB}}$= 17°, $\widehat{\mathrm{ABD}}$= 90°.
$\widehat{\mathrm{ACB}}$= 180° – $\widehat{\mathrm{CAB}}$ – $\widehat{\mathrm{ABD}}$ = 180° – 17° – 90° = 73° (tổng ba góc một tam giác bằng 180°).
$\widehat{\mathrm{ACD}}$ = 180° – $\widehat{\mathrm{ACB}}$= 180° – 73° = 107°
Tam giác ABC vuông tại B ⇒ AC = $\frac{\mathrm{AB}}{\cos \widehat{\mathrm{CAB}}}$= $\frac{72}{\cos 17°}$≈ 75,3 (m)
Áp dụng định lí côsin trong tam giác ACD, ta có:
AD² = AC² + CD² – 2AC.CD.$\cos \widehat{\mathrm{ACD}}$
         = (75,3)² + 20² – 2.75,3.20.cos107° ≈ 6950,7
AD = 83,4m
Vậy chiều dài của dây cáp là 83,4m.
B.2 Bài tập trắc nghiệm
Câu 1. Tam giác ABC có a = 21, b = 17, c = 10. Diện tích của tam giác ABC bằng:
A. ${\mathrm{S}}_{\mathrm{\Delta ABC}}=16$;     
B. ${\mathrm{S}}_{\mathrm{\Delta ABC}}=48$;    
C. ${\mathrm{S}}_{\mathrm{\Delta ABC}}=24$;    
D. ${\mathrm{S}}_{\mathrm{\Delta ABC}}=84$.
Hướng dẫn giải
Đáp án đúng là: D
Ta có:
Nửa chu vi của tam giác ABC là:
$\mathrm{p}=\frac{21+17+10}{2}=24$ (đvđd).
Do đó
Diện tích tam giác ABC là:
 $\mathrm{S}=\sqrt{\mathrm{p}\left(\mathrm{p}-\mathrm{a}\right)\left(\mathrm{p}-\mathrm{b}\right)\left(\mathrm{p}-\mathrm{c}\right)}=\sqrt{24.\left(24-21\right).\left(24-17\right).\left(24-10\right)}=84$ (đvdt).
Câu 2. Tam giác ABC có AB = 8 cm, AC = 18 cm và có diện tích bằng 64 cm². Giá trị sinA bằng:
A. $\mathrm{sinA}=\frac{\sqrt{3}}{2}$;   
B. $\mathrm{sinA}=\frac{3}{8}$;      
C. $\mathrm{sinA}=\frac{4}{5}$;      
D. $\mathrm{sinA}=\frac{8}{9}$.
Hướng dẫn giải
Đáp án đúng là: D
Ta có:
 ${\mathrm{S}}_{\mathrm{\Delta ABC}}=\frac{1}{2}.\mathrm{AB}.\mathrm{AC}.\mathrm{sinA}\iff 64=\frac{1}{2}\mathrm{.8.18.}\mathrm{sinA}\iff \mathrm{sinA}=\frac{8}{9}.$ 
Câu 3. Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng:
A. $13{\text{ cm}}^{\text{2}}$;          
B. $13\sqrt{2}{\text{ cm}}^{\text{2}}$;     
C. $12\sqrt{3}{\text{ cm}}^{\text{2}};$     
D. $15{\text{ cm}}^{\text{2}}$.
Hướng dẫn giải
Đáp án đúng là: C
Xét tam giác ABC đều, có độ dài cạnh bằng a.

Theo định lí sin, ta có: $\frac{\mathrm{BC}}{\sin \widehat{\mathrm{BAC}}}=2\mathrm{R}\iff \frac{\mathrm{a}}{\sin 60°}=2.4\iff \mathrm{a}=8.\sin 60°=4\sqrt{3}$ (đvđd).
Vậy diện tích tam giác ABC là:
 ${\mathrm{S}}_{\mathrm{\Delta ABC}}=\frac{1}{2}.\mathrm{AB}.\mathrm{AC}.\sin \widehat{\mathrm{BAC}}=\frac{1}{2}.{\left(4\sqrt{3}\right)}^2.\sin 60°=12\sqrt{3}{\mathrm{cm}}^2.$

Bài giảng Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác – Cánh diều

====== ****&**** =====